 |
Решение краевых задач методом конечных элементов
|
|
|
|
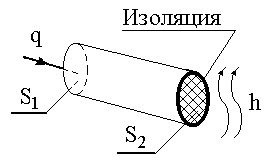
Постановка задачи. Выберем в качестве ИТО одномерный стержень с коэффициентом теплопроводности l, показанный на рисунке 11.1-а. Стержень имеет теплоизолированную боковую поверхность. К левому концу стержня подводится тепловой поток заданной интенсивности q (Вт/см2). На правом конце стержня происходит конвективный обмен тепла с коэффициентом теплообмена – h (Вт/см2 оС). Температура окружающей среды – Тос (оС). Поскольку стержень теплоизолирован, потерь тепла через боковую поверхность не происходит. Требуется определить температурное поле вдоль стержня в установившемся режиме.
Известно, что для данной модели распределение температуры внутри стержня описывает следующее дифференциальное уравнение:
| l | д 2T | = 0 | (11.1) | ||||
| дx 2 | |||||||
|

| ||||||
| a) | б) | ||||||
| Рис. 10.1 | |||||||
При этом, поскольку в установившемся режиме в точках приложения (при х =0) и отвода (х =L) тепла тепловая энергия не должна «задерживаться», должны быть соблюдены следующие граничные условия:
– на левом конце стержня (х=0):
| l | д T | + q = 0 | (11.2) |
| дx |
– на правом конце стержня (х=L):
| l | д T | + h (T – TОС) = 0 | (11.3) |
| дx |
Если тепло отводится от стержня, тепловой поток q должен быть положителен, в противном случае – отрицателен.
Исследования методами вариационного исчисления показывают, что с математической точки зрения в интересующем нас установившемся режиме должен достигать минимума следующий функционал:
| c = | òV | l | [ | д T | ] | dV + | òS | [ | QT + | h | (T – TOC)2 | ] | dS | (11.4) | |
| дx |
Учитывая, что боковая поверхность стержня теплоизолирована, приведенный функционал можно представить в следующем виде:
| c = | òV | l | [ | д T | ] | dV + | òS1 | (qT) d S + | òS2 | h | (T – TOC)2 d S | (11.5) | |
| дx |
С физической точки зрения функционал (11.5) моделирует непрерывность теплового потока в установившемся тепловом режиме. Это означает, что в любой момент времени сумма подводимой (через поверхность S1) к стержню и рассеиваемой им (через поверхность S2) тепловой энергии равна энергии, сосредоточенной в объеме (V) стержня. В противном случае, не отводимый от стержня избыток тепловой энергии будет продолжать нагревать стержень, что противоречит условию установившегося режима.
|
|
|
Поскольку, с одной стороны, установившийся режим описывается дифференциальным уравнением (11.1) с граничными условиями (11.2 и 11.3), а, с другой стороны, функционал (11.4) достигает минимума именно в установившемся режиме, то минимум функционала (11.4) и является решением ДУ (11.1) с граничными условиями (11.3).
Температура стержня во всех точках сечения S1 (S2) одинакова и равна неизвестной пока (но постоянной в стационарном режиме) величине – Т1 (Т3). Учитывая, что в данном случае S1 = S2 = A и в силу сказанного, выражение (11.5) принимает вид:
| qT1 | òS1 | d S + | h | (T3 – TOC)2 | òS2 | d S = | qT1А + | h | (T3 – TOC)2 А | (11.6) |
Таким образом, исходное уравнение для определения температуры в каждой точке стержня методом МКЭ примет вид:
| c = | òV | l | [ | д T | ]2 | d V + | qT1А + | h | (T3 – TOC)2 А | (11.7) |
| дx |
Реализация метода МКЭ включает этапы:
1. Определение подобластей (конечных элементов) и их узловых точек. В данном случае, стержень может быть разбит на два одномерных симплекс – элемента, как это показано на рисунке (10.1-б) с узловыми значениями Т1, Т2 и Т3. Температура внутри элементов находится из формул:
| T[1] = N1[1] T1 + N2[1] T2 ; | T[2] = N2[2] T2 + N3[2] T3 ; | (11.8) |
ФФ здесь согласно (9.5) равны:
| N1[1] | = | (X2 – x) | ; | N2[1]= | (x – X1) | ; |
| L[1] | L[1] | |||||
| N2[2] | = | (X3 – x) | ; | N3[2]= | (x – X2) | |
| L[2] | L[2] |
2. Вычисление частных производных, входящих в выражение (11.7):
|
|
|
| д T[1] | = | (-T1+T2); | д T[2] | = | (-T2+T3) | (11.9) | ||
| дx | L[1] | дx | L[2] |
3. Разделение интеграла в выражении (11.7) на два (по числу подобластей – конечных элементов, выделенных в пункте 1). Необходимость разбиения интеграла продиктована тем, что производная температуры по переменной х (градиент температуры по оси ОХ), входящая под знак интеграла, не является непрерывной в точке Т3. Учитывая, что dV=Adx, где А – площадь сечения стержня (А1 = А2 = А3 =А), после разделения и подстановки пределов интегрирования получаем выражение:
| x2 | x3 | ||||||||||||||||||||||||||
| ò | l | [ | д T | ]2 | d V = | l[1]A[1] | ò | [ | д T | ]2dx + | l[2]A[2] | ò | [ | д T | ]2dx | (11.10) | |||||||||||
| дx | дx | дx | |||||||||||||||||||||||||
| V | x1 | x2 | |||||||||||||||||||||||||
4., Проведение подстановки (11.9) в (11.10) и интегрирование:
| ò V | l | [ | д T | ]2 | d V = | l[1]A[1] | [-T1+T2]2 + | l[2]A[2] | [-T2+T3]2 | (11.11) |
| дx | 2L[1] | 2L[2] |
5. Выражаем функционал через узловые значения температуры, для чего объединяем выражения (11.7) и (11.11):
| c = | C[1] | (-T1+T2)2 + | C[2] | (-T2+T3)2 +qA[1]T1 + | hA[3] | (-T3+TOC)2 | (11.12) | |
Здесь приняты следующие обозначения:
С(1) = (А(1)l(1)/L(1)); С(2) = (А(2)l(2)/L(2))
6. Получение системы алгебраических уравнений. Правильными значениями Т1, Т2 и Т3 являются те, при которых величина функционала c достигает минимума. Приравнивая нулю первую производную функционала (11.12) по Т1, получаем первое уравнение системы:
| д c | = C[1] T1 - C[1] T2 + qA[1] = 0 | (11.13) | |
| д T1 |
Аналогично получаем еще два уравнения:
| д c | = -C[1] T1 + [C[1] +C[2] ]T2 -C[2] T3 = 0 | (11.14) | |
| д T2 | |||
| д c | = -C[2] T2 + [C[3] +hA3 ]T3 - hA3TOC = 0 | ||
| д T3 |
Запишем полученную систему в матричной форме:
| С(1) | -С(1) | Т1 | -qA1 | ||||
| -С(1) | С(1)+С(2) | -С(2) | Т2 | = | (11.15) | ||
| -С(2) | С(2)+hA3 | Т3 | hA3TOC |
В более общей матричной форме система примет вид:
| C | · | T | = | F | (11.16) |
Матрица C в формуле (11.16) называется «глобальной матрицей жесткости». В контексте задачи переноса тепла –это – «глобальная матрица теплопроводности». Вектор-столбец F называется «глобальным вектором нагрузки». Искомый вектор [T] будем называть вектором решения.
Пример 11.1. Рассчитать температурное поле в круглом стержне с площадью поперечного сечения A=1 см2 и длиной L=7,5 см с теплоизолированными стенками. К левому концу стержня подводится тепловой поток q = 150 Вт/см2. Коэффициент теплопроводности материала стержня и коэффициент конвективного теплообмена на правом конце стержня соответственно равны: l=75 Вт/(см · ОС), h = 10 Вт/(см2 · ОС). Температура окружающей среды равна ТОС=40 ОС.
|
|
|
Решение.
1. Тепло подводится к стержню, поэтому тепловой поток q следует записывать со знаком «минус»: q = - 150 Вт/см2.
2. Рассчитываем значение термов, входящих в коэффициенты матриц C и F:
С(1) =(А(1)l(1)/L(1))=(1·75/3,75)=20Вт/(см·ОС),
С(2) =(А(2)l(2)/L(2))=(1·75/3,75)=20Вт/(см·ОС),
hA3=10Вт/(см·ОС), -qA1= -(-150)·1 = 150Вт/см,
hA3TOC=10·1·40 = 400Вт/см.
3. Окончательная система уравнений примет вид:
| -20 | Т1 | ||||||
| -20 | -20 | · | Т2 | = | |||
| -20 | Т3 |
4. Решением полученной системы являются следующие узловые значения температуры: Т1=70 оС, Т2=62,5 оС; Т3=55 оС.
Метод граничных элементов
Наряду с методами МКР и МКЭ для количественного анализа ММ, описываемых системой ДУ в частных производных весьма перспективным является метод граничных элементов (МГЭ) [11]. Для применения МГЭ математическую модель процесса необходимо предварительно привести к форме, содержащей граничные интегральные уравнения с неизвестными распределениями искомых параметров на границе области, в которой протекает рассматриваемый процесс. Это позволяет понизить размерность задачи и сэкономить вычислительные ресурсы.
Вывод граничных интегральных уравнений и их решение могут оказаться более сложными математически, чем прочие упомянутые выше методы. Однако, несмотря на то, что методы граничных интегральных уравнений в прошлом развивались лишь математиками, в настоящее время эти методы широко применимы без использования доказательств существования и единственности для каждого отдельного решения. В результате они стали очень популярны и в настоящее время реализованы в ряде зарубежных и отечественных систем (Ansys Nastran, Adams, T-Flex-Динамика, Динамика-2 и др.).
Хотя все МГЭ имеют общее происхождение, они делятся на три различные, но тесно связанные между собой категории.
|
|
|
Прямой вариант МГЭ. В этом варианте неизвестные функции, входящие в интегральные уравнения, являются реальными, имеющими физический смысл переменными задачи. Так, например, в задачах теории упругости такое решение интегрального уравнения должно сразу давать все усилия и смещения на границе, а внутри тела они должны быть получены из граничных значений численным интегрированием. Алгоритмы, основанные на прямом подходе, известны как методы граничных интегральных уравнений.
Непрямые варианты МГЭ. В непрямом варианте интегральные уравнения полностью выражаются через фундаментальное сингулярное решение исходных ДУ, распределенное с неизвестной плотностью по границам рассматриваемой области. Напомним, что математическая сингулярность – это точка, в которой математическая функция стремится к бесконечности. Сами по себе функции плотности не имеют определенного физического смысла, но, когда они найдены (численным решением интегральных уравнений), значения параметров решения везде внутри тела могут быть получены из них простым интегрированием.
Полупрямые варианты МГЭ. В качестве альтернативы можно составлять интегральные уравнения для неизвестных функций, аналогичных функциям напряжений в теории упругости. Когда получено решение для этих функций, простое дифференцирование даст, например, распределение внутренних напряжений.
Все методы граничных элементов используют принцип суперпозиции и поэтому применимы или к полностью линейным системам либо к системам, линейным относительно приращений до или после их аппроксимации. При этом МГЭ моделирует только граничную геометрию системы, и как только получена необходимая информация о границе, сразу могут быть вычислены значения переменных во внутренних точках.
Само по себе граничное интегральное уравнение является формулировкой поставленной задачи, ведущей к точному ее решению. Погрешности дискретизации ее решения имеют место только на границах области. При выборе криволинейных граничных элементов указанные погрешности оказываются действительно очень малыми. Это объясняется тем, что численное интегрирование, с которым оперируют прямой и непрямой МГЭ, всегда представляет собой более точный (и устойчивый) процесс, чем численное дифференцирование, которое указанные методы граничных элементов не используют.
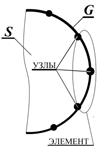
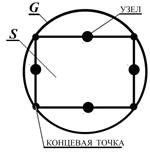
Типы граничных элементов. Пусть требуется найти решение ДУ внутри некоторой области S с границей G. Сущность МГЭ состоит в дискретизации границы конечным числом сегментов, не обязательно равных, которые называются граничными элементами. Для каждого их граничных элементов сделаны два приближения: первое связано с геометрией границы, а другое касается изменения неизвестной граничной величины на граничном элементе. На практике обычно используются:
|
|
|
- постоянный граничный элемент;
- линейный граничный элемент;
- параболический или квадратичный граничный элемент.
На граничных элементах каждого типа выделяются крайние или концевые узловые точки (узлы), в которых определяются искомые значения граничных величин.
Для постоянных граничных элементов граничный сегмент аппроксимируется прямой линией, которая соединяет его крайние точки. Узел помещается в середине прямой линии, а граничная величина принимается постоянной вдоль всего граничного элемента и равной значению в узловой точке (рис.3.6,а).
Линейный граничный элемент также представляется прямой линией, которая соединяет его конечные точки. Элемент имеет два узла, которые обычно помещаются в его крайние точки. Граничная величина линейно изменяется между узловыми значениями (рис.3.6,б).
Геометрия параболического граничного элемента приближена к параболической дуге. Элемент имеет три узла, два из которых помещены на концах, а третий обычно посередине элемента, (рис.3.6,в).


а) б) в)
Рис.3.6
Расчет тепловых режимов методом граничных элементов. Рассмотрим однородный объект длиной L и сечением S, ограниченный точками Q и P (рис.3.7), температуру в которых обозначим соответственно T(Q) и T(P). В точке приложения нагрузки (В) с координатой x находится точечный источник тепла интенсивности q = q (В). Точка наблюдения или точка поля (P') имеет абсциссу x.
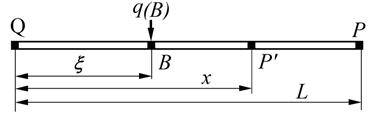
Рис.3.7
В одномерном приближении температура T(x) во всех внутренних точках удовлетворяет уравнению Лапласа:
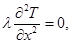 (3.23)
(3.23)
а тепловой поток:
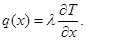 (3.24)
(3.24)
При нулевых граничных условиях решение уравнений (3.23 и 3.24) в любой точке объекта, кроме x= x, можно записать в виде [2]:
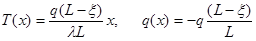 при
при 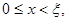 (3.25)
(3.25)
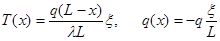 при
при 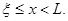 (3.26)
(3.26)
При x=x величина 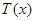 однозначно определяется из (3.25) и/или (3.26), а
однозначно определяется из (3.25) и/или (3.26), а 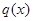 меняется скачком, равным
меняется скачком, равным 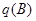 , при переходе точки наблюдения через точку приложения нагрузки.
, при переходе точки наблюдения через точку приложения нагрузки.
Пример 2. Построить график изменения температуры 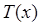 и интенсивности теплового потока
и интенсивности теплового потока 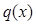 вдоль цилиндрического стержня с теплоизолированными боковыми стенками, если его длина
вдоль цилиндрического стержня с теплоизолированными боковыми стенками, если его длина 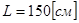 , площадь поперечного сечения
, площадь поперечного сечения 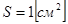 и в сечении на расстоянии
и в сечении на расстоянии  от левого конца действует источник тепла интенсивностью
от левого конца действует источник тепла интенсивностью 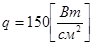 . За счет внешних сил температура в граничных точках поддерживается равной нулю. Коэффициент теплопроводности материала стержня принять равным
. За счет внешних сил температура в граничных точках поддерживается равной нулю. Коэффициент теплопроводности материала стержня принять равным 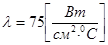 .
.
Решение. На участке стержня 0£ x< x, функция 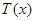 в выражении(3.25) линейна относительно
в выражении(3.25) линейна относительно 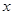 , поэтому график
, поэтому график 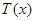 представляет прямую линию. Так как
представляет прямую линию. Так как 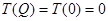 (по условию задачи), тодля ее построения достаточно найти ординату
(по условию задачи), тодля ее построения достаточно найти ординату 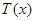 в точке x= x:
в точке x= x:
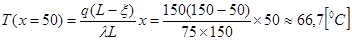 .
.
На этом же участке интенсивность теплового потока, согласно (3.25) постоянна и равна:
 .
.
Тепловой поток подводится к стержню (в точке В) и поэтому взят со знаком минус.
Вычисления для участка 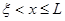 выполняются аналогично. На рис.3.8 приведены искомые графики, на которых наглядно видно, что полученное решение является сингулярным (то есть содержит точку разрыва в месте действия внешнего источника тепла).
выполняются аналогично. На рис.3.8 приведены искомые графики, на которых наглядно видно, что полученное решение является сингулярным (то есть содержит точку разрыва в месте действия внешнего источника тепла).
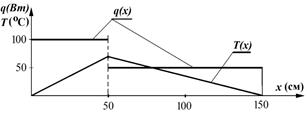
Рис.3.8
Если в уравнения (3.25) и (3.26) подставить 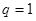 , то функции
, то функции 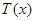 и
и 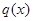 , которые в них фигурируют, могут выступать в качестве функций влияния источника на величины соответственно температуры и теплового потока в точке наблюдения. Функции влияния лежат в основе любого варианта использования МГЭ, который позволяет объединить отклики системы на единичные возмущения, приложенные во внутренних точках сплошной среды, посредством использования принципа суперпозиции, получив в результате искомое решение.
, которые в них фигурируют, могут выступать в качестве функций влияния источника на величины соответственно температуры и теплового потока в точке наблюдения. Функции влияния лежат в основе любого варианта использования МГЭ, который позволяет объединить отклики системы на единичные возмущения, приложенные во внутренних точках сплошной среды, посредством использования принципа суперпозиции, получив в результате искомое решение.
Поиск решения с помощью МГЭ состоит из пяти этапов:
- получение фундаментальных решений для неограниченной области;
- вывод соотношений, связывающих неизвестные и заданные узловые значения в области S с границей G;
- получение дополнительных энергетических соотношений;
- решение полученной в пунктах 2 и 3 системы уравнений;
- вычисление неизвестных узловых значений.
Рассмотрим более подробно шаги реализации метода граничных элементов на примере вычисления температурного поля одномерного стержня.
Получение фундаментальных решений для неограниченной области (рис.3.9). Непосредственно в неограниченных системах можно определить не саму функцию 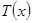 , а лишь ее отклонение относительно некоторого фиксированного значения. Примем в качестве такого значения величину температуры
, а лишь ее отклонение относительно некоторого фиксированного значения. Примем в качестве такого значения величину температуры 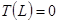 в сечениях
в сечениях 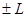 стержня.
стержня.

Рис.3.9
По аналогии с выражением (3.25), тепловой поток  [Вт/см2], действующий в сечении
[Вт/см2], действующий в сечении 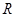 [см], поднимет температуру в сечении
[см], поднимет температуру в сечении 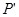 стержня
стержня  на величину:
на величину:
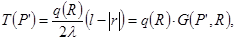 (3.27)
(3.27)
где 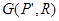 – выражение, в котором сгруппированы все члены равенства кроме
– выражение, в котором сгруппированы все члены равенства кроме  . Это выражение представляет оператор, зависящий от упорядоченной пары
. Это выражение представляет оператор, зависящий от упорядоченной пары  ,причемтакой, что, будучи умноженный на
,причемтакой, что, будучи умноженный на  , даст значение температуры в точке
, даст значение температуры в точке 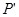 . Переходя далее к абсолютным координатам, перепишем (3.27) в виде:
. Переходя далее к абсолютным координатам, перепишем (3.27) в виде:
T (х) = q( x ) G(x, x ). (3.28)
Обозначим 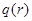 – тепловой поток в точке на расстоянии
– тепловой поток в точке на расстоянии  от источника. Учитывая выражение (3.24) и дифференцируя (3.27):
от источника. Учитывая выражение (3.24) и дифференцируя (3.27):
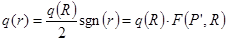 , (3.29)
, (3.29)
где выражение 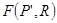 , в котором сгруппированы все члены равенства кроме
, в котором сгруппированы все члены равенства кроме  , представляет собой оператор, зависящий от упорядоченной пары
, представляет собой оператор, зависящий от упорядоченной пары  , причемтакой, что, будучи умноженный на
, причемтакой, что, будучи умноженный на  , даст значение интенсивности потока в сечении
, даст значение интенсивности потока в сечении 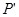 . Переходя далее к абсолютным координатам, перепишем (3.29) в виде:
. Переходя далее к абсолютным координатам, перепишем (3.29) в виде:
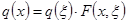 . (3.30)
. (3.30)
Функция 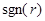 принимает значение +1 (–1) в сечениях справа (слева) от источника теплового потока
принимает значение +1 (–1) в сечениях справа (слева) от источника теплового потока 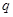 (рис.3.8). В самой же точке приложения потока функция
(рис.3.8). В самой же точке приложения потока функция 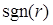 не определена, что позволяет автоматически учесть скачкообразное изменение
не определена, что позволяет автоматически учесть скачкообразное изменение 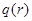 при
при 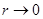 .
.
Поместим реальный ТО (рис.3.10) в неограниченную систему (рис.3.11).
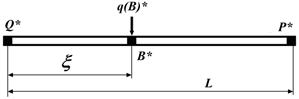 Рис.3.10
Рис.3.10
| 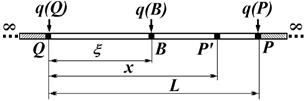 Рис.3.11
Рис.3.11
|
На рисунке 3.10 реальные значения параметров в отличие от тех же параметров в неограниченной системе помечены звездочками. Поскольку границами одномерной области 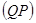 являются просто ее две точки
являются просто ее две точки 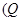 и
и  , достаточно ввести в этих точках по одному граничному элементу. Далее в обоих граничных элементах введем фиктивные источники неизвестной пока интенсивности
, достаточно ввести в этих точках по одному граничному элементу. Далее в обоих граничных элементах введем фиктивные источники неизвестной пока интенсивности 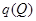 и
и 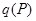 . Ясно, что влияние введенных источников на каждую внутреннюю точку
. Ясно, что влияние введенных источников на каждую внутреннюю точку 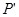 может быть выражено в виде (3.28 и 3.30). Каждый из источников:
может быть выражено в виде (3.28 и 3.30). Каждый из источников: 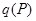 ,
, 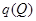 и
и 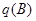 , показанных на рис.3.11, оказывает влияние на сечение в точке
, показанных на рис.3.11, оказывает влияние на сечение в точке 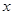 . Принцип суперпозиции позволяет оценить суммарное их действие в виде:
. Принцип суперпозиции позволяет оценить суммарное их действие в виде:
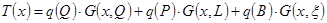 , (3.31)
, (3.31)
 . (3.32)
. (3.32)
Полученные равенства справедливы для любой точки наблюдения в пределах отрезка 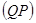 . Выберем в качестве таковой точку левее точки
. Выберем в качестве таковой точку левее точки 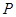 , то есть точку с абсциссой
, то есть точку с абсциссой  при
при 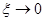 . По формулам (3.27 и 3.31) находим температуру в точках
. По формулам (3.27 и 3.31) находим температуру в точках 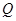 и
и 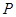 :
:
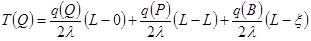 .
.
После очевидных упрощений получим:
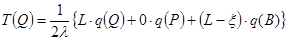 . (3.33)
. (3.33)
Аналогично находим 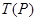 :
: 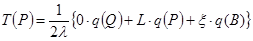 . По формулам (3.29 и 3.32) находим интенсивность потока в точках
. По формулам (3.29 и 3.32) находим интенсивность потока в точках 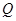 и
и 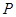 :
:
 (3.34)
(3.34)
Потребуем теперь, чтобы граничные условия в точках 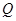 и
и 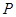 фиктивной системы в точности совпадали с условиями реальной задачи. С этой целью в уравнениях (3.33 и 3.34) сделаем замену:
фиктивной системы в точности совпадали с условиями реальной задачи. С этой целью в уравнениях (3.33 и 3.34) сделаем замену: 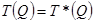 и
и 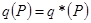 , после чего они примут вид:
, после чего они примут вид:
 (3.35)
(3.35)
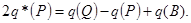 (3.36)
(3.36)
Решая систему (3.35) и (3.36), получим обе неизвестные величины: 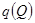 и
и 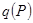 , которые после подстановки в выражения (3.31 и 3.32) позволят вычислить лишь относительные значения искомых величин, как это ясно из раздела «п олучение фундаментальных решений». Для обеспечения единственности решения потребуем, чтобы обращался в нуль полный поток через бесконечно удаленные границы, что эквивалентно обращению в 0 суммы потоков
, которые после подстановки в выражения (3.31 и 3.32) позволят вычислить лишь относительные значения искомых величин, как это ясно из раздела «п олучение фундаментальных решений». Для обеспечения единственности решения потребуем, чтобы обращался в нуль полный поток через бесконечно удаленные границы, что эквивалентно обращению в 0 суммы потоков 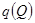 ,
, 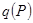 и
и  . С этой целью в выражении (3.27) заменим источник
. С этой целью в выражении (3.27) заменим источник  на источник
на источник 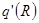 . Замена вызовет коррекцию температуры на заранее неизвестную константу
. Замена вызовет коррекцию температуры на заранее неизвестную константу  , после чего выражение (3.27) примет вид:
, после чего выражение (3.27) примет вид:
 ,
,
и вытекающие из него уравнения (3.35 и 3.36) так же изменятся и дополнятся условием равенства нулю суммы всех потоков, включая модифицированные:

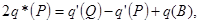

В матричной форме данная система уравнений примет вид:
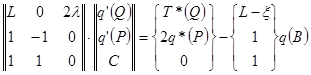 ,
,
Решение системы дает выражения для вычисления 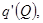
 и
и  :
:
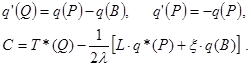 (3.37)
(3.37)
Подставив эти равенства в уравнения (3.31, 3.32), мы сможем вычислить 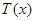 и
и 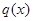 в любой точке
в любой точке 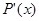 внутри интервала
внутри интервала 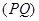 .
.
Так, при  из равенств (3.27 и 3.31) имеем:
из равенств (3.27 и 3.31) имеем:
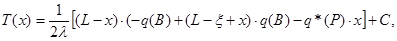
откуда с учетом (104) значения 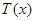 и
и 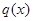 соответственно равны:
соответственно равны:

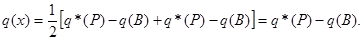
Аналогично на интервале  имеем:
имеем:
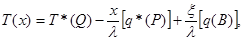 (3.38)
(3.38)
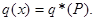 (3.39)
(3.39)
Пример 3. Рассчитать температурное поле и интенсивность теплового потока в круглом стержне с теплоизолированными стенками сечением 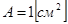 и длиной
и длиной 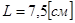 . Температура на левом конце стрежня поддерживается постоянной и равной
. Температура на левом конце стрежня поддерживается постоянной и равной 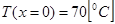 . Тепловой поток, отводящий тепло от правого конца стержня, равен
. Тепловой поток, отводящий тепло от правого конца стержня, равен 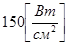 . Коэффициент теплопроводности стержня l=75 Вт/(см ОС).
. Коэффициент теплопроводности стержня l=75 Вт/(см ОС).
Решение. Из формулы (3.39) получаем 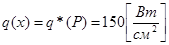 и, так как на интервале
и, так как на интервале 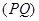 внутри стержня источников тепла нет, то
внутри стержня источников тепла нет, то 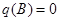 и формула (3.38) примет вид:
и формула (3.38) примет вид:
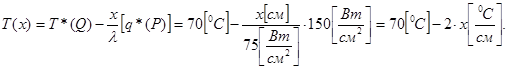
Таким образом, температура линейно убывает и на правом конце стержня составит: 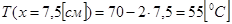 .
.
Решение этой задачи методом конечных элементов, приведенное далее в разделе 5 дает такие же результаты.
Типы граничных элементов.
Пусть требуется найти решение ДУ внутри некоторой области S с границей G. Сущность МГЭ состоит в дискретизации границы конечным числом сегментов, не обязательно равных, которые называются граничными элементами. Для каждого их граничных элементов сделаны два приближения: первое связано с геометрией границы, а другое касается изменения неизвестной граничной величины на граничном элементе. На практике обычно используются:
- постоянный граничный элемент;
- линейный граничный элемент;
- параболический или квадратичный граничный элемент.
На граничных элементах каждого типа выделяются крайние или концевые узловые точки (узлы), в которых определяются искомые значения граничных величин.
Для постоянных граничных элементов граничный сегмент аппроксимируется прямой линией, которая соединяет его крайние точки. Узел помещается в середине прямой линии, а граничная величина принимается постоянной вдоль всего граничного элемента и равной значению в узловой точке (рис.3.6,а).
Линейный граничный элемент также представляется прямой линией, которая соединяет его конечные точки. Элемент имеет два узла, которые обычно помещаются в его крайние точки. Граничная величина линейно изменяется между узловыми значениями (рис.3.6,б).
Геометрия параболического граничного элемента приближена к параболической дуге. Элемент имеет три узла, два из которых помещены на концах, а третий обычно посередине элемента, (рис.3.6,в).
а) б) в)
|
|
|


