 |
Двумерный симплекс-элемент.
|
|
|
|
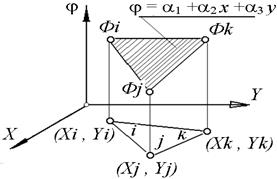
Двумерный симплекс – элемент показан на рисунке 9.3 – это треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине. Примем последовательную логическую нумерацию узлов элемента против часовой стрелки, начиная от произвольно выбранного i-го узла. Узловые значения скалярной величины j обозначим через Фi, Фj, Фk, а координатные пары трех узлов - через (Xi, Yi), (Xj, Yj), (Xk, Yk).
| 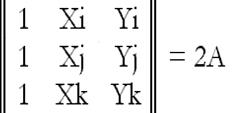
|
| Рис. 5.3 | Рис. 5.4 |
Интерполяционный полином в данном случае примет вид:
j = a1 +a2 x +a3 y (5.7)
В узлах выполняются следующие условия: j = Фi при x = Xi и y = Yi
j = Фj при x = Xj и y = Yj j = Фk при x = Xk и y = Yk
Подстановка их в (9.7) приводят к системе трех уравнений:
Фi = a1 + a2 Xi + a3 Yi
Ф j = a1 + a2 Xj + a3 Yj (9.8)
Фk = a1 + a2 Xk + a3 Yk
Обозначим площадь симплекс – треугольника буквой А. Можно показать, что определитель системы (9.8) связан с А (рис. 5.4) соотношением:
[XjYk – XkYj + XiYj – XiYk + XkYi – XjYi] =2A
Решая систему (9.8) с учетом (9.8) и вводя обозначения:
Ai=(Xj Yk – Xk Yj); Bi=(Yj – Yk); Ci=(Xk – Xj),
Aj = (Xk Yi – Xi Yk), Bj = (Yk – Yi), Cj =(Xi – Xk), (9.9)
Ak =(Xi Yj – Xj Yi), Bk = (Yi – Yj), Ck = (Xj – Xi),
получим значения искомых коэффициентов:
a1 = 0,5 А –1 [ Ai Фi + Aj Фj + Ak Фk ]
a2 = 0,5 А –1 [ Bi Фi + Bj Фj + Bk Фk ]
a3 = 0,5 А –1 [ Ci Фi + Cj Фj + Ck Фk ]
Подставляя значения a1, a2, a3 в (9.7) и преобразуя получаемые выражения к виду, подобному (9.6), получим выражение для скалярной величины j:
j = Ni Фi + Nj Фj + Nk Фk (9.10)
где:
| Ni = | Ai+Bi x +Ci y | ; Nj = | Aj+Bj x +Cj y | ; Nk = | Ak+Bk x +Ck y | (9.11) |
| 2A | 2A | 2A |
Значение Ni в i-м узле составит: Ni = 0,5 А –1 [Ai + Bi x + Ci y ] =
= 0,5 А –1 [Xj Yk – Xk Yj + (Yj – Yk) Xi + (Xk – Xj) Yi] =
= 0,5 А –1 [XjYk – XkYj + XiYj – XiYk + XkYi – XjYi] = 1
Непосредственной проверкой можно показать, что в остальных узлах Ni = 0.
Из (9.11) видно, что ФФ линейны по x и y, то есть, градиенты этой величины в направлениях Ox и Oy будут постоянны. Заметим, что:
|
|
|
| д Nb | = Вb | (b = j, j, k) | |
| дx |
поэтому градиент j в направлении оси Ох составит:
| д Ф | = | д Ni | Фi + | д Ni | Фj + | д Nk | Фk = | BiФi + BjФj + BkФk | (9.12) |
| дx | дx | дx | дx |
Поскольку, переменные Вb и величины Фb начальных условий (при b = i, j, k) фиксируются, как только задаются узловые координаты, то частная производная в (9.12) имеет постоянное значение. Отсюда следует важный вывод: постоянство градиента внутри каждого элемента означает, что необходимо применять очень малые по величине элементы, чтобы аппроксимировать быстро меняющую функцию j.
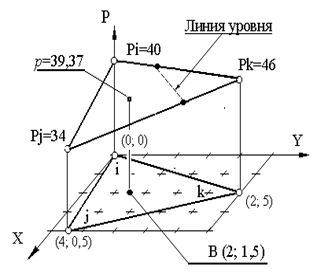
Пример 9.2. Требуется получить соотношение, определяющее элемент, и вычислить значение давления в точке В с координатами (2; 1,5), если заданы начальные значения: Pi = 40 H/см2, Pj = 34 H/см2, Pk = 46 H/см2.
Давление р внутри элемента определяется по формуле: р = Ni Рi + Nj Рj + Nk Рk
где ФФ Ni, Nj и Nk определяются по (9.11).
Подставляя значения координат узлов в обозначения (9.9) для Аb, Вb, Сb (при b = i, j, k), получим значения этих коэффициентов:
Ai = (4·5)–(2·1,5) = 19; Aj = (2·0) –(0·5) = 0; Ak =(0·0,5)–(4·0) = 0;
Bi = (0,5–5) = – 4,5; Bj = (5 – 0) = 5; Bk =(0 – 0,5) = – 0,5;
Ci = (2–4) = – 2; Cj = (0 – 2) = – 2; Ck =(4– 0) = 4;
| 
|
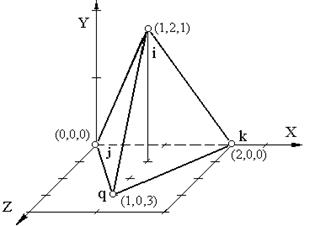
| Рис. 9.4 | Рис. 9.5 |
Вычисляем определитель:
| 2A= | Xi | Yi | = | |||||
| Xj | Yj | 0,5 | =20-1=19 | |||||
| Xk | Yk |
После подстановки констант в ФФ выражение для р примет вид:
| p = | [(19–4,5x–2y)Pi + (5x – 2y)Pj + (– 0,5x + 4y) Pk |
Значение давления в точке В с координатами (2; 1,5) равно:
| p = | 7·40 +7·34 +5·46 | = 39,37 Н/см2 |
Отметим два полезных свойства треугольного элемента. Во-первых, функция j изменяется линейно между двумя любыми узлами. Так как узлы определяют границы элемента, j меняется линейно вдоль каждой из трех его сторон. Отсюда следует второе полезное свойство: любая линия, вдоль которой j принимает одинаковые значения, есть прямая линия, пересекающая две стороны элемента. Исключением будет случай, когда во всех узлах значения j одинаковые. Приведенные два свойства позволяют легко определять линии уровня скалярной величины. Обратимся к предыдущему примеру, чтобы проиллюстрировать эти свойства.
|
|
|
|
|
|


