Основные положения, выносимые на защиту 12 глава

Dw_i(nDt) – отклонение от номинального значения за счет эффекта Доплера частоты сигнала, пришедшего в точку приема i-м лучом.

В (nDt)-ый момент времени значения начальной фазы сигнала, пришедшего в точку приема i -м лучом, описываются выражением:

j_i(nDt) = j(nDt-Dn_i) + j^*_i(nDt), (4.6.6)

где j(nDt) - закон изменения фазы сигнала на передающем конце радиолинии, j^*_i(nDt) - изменение начальной фазы сигнала в i -м луче.

Отсчеты квадратур результирующего сигнала на выходе тракта промежуточной частоты приемного устройства являются совокупностью отсчетов компонентов, которые приходят в точку приема различными лучами. Поэтому можно записать:

(4.6.7)

где I - общее количество лучей.

Отсчеты квадратур шума являются случайными величинами, распределенными по нормальному закону. Корреляция между отдельными отсчетами соответствующих квадратур обусловливается полосой пропускания тракта промежуточной частоты приемника D F. Интервал корреляции Т _о может быть оценен следующим образом [96]:

Т _о = 1/2D F. (4.6.8)

Представляя последовательность отсчетов каждой из квадратур шума, взятую с периодом D t, в виде марковской [165], можно принять значение коэффициента корреляции r (Dt) равным:

r (Dt) = exp(-D t / T _o). (4.6.9)

Зная спектральную плотность мощности шума , можно найти среднеквадратическое отклонение s_ш шума на выходе тракта приемного устройства, имеющего полосу пропускания DF:

. (4.6.10)

Формирование отсчетов квадратурных компонентов шума производится по алгоритму [134]:

(4.6.11)

где _шc(n) и 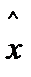_шs(n) - первообразующие нормальные центрированные и нормированные некоррелированные случайные процессы, которые формируются аналогично тому, как это описано в первой главе.

Отсчеты квадратур станционных помех принципиально не отличаются от отсчетов сигнала или шума. В модели принято две градации станционных помех. Первая градация относится к варианту, когда спектр станционной помехи попадает в полосу пропускания тракта частично. В этом случае отсчеты квадратур формируются точно также, как и отсчеты квадратур шумового компонента с соответствующим среднеквадратическим отклонением. Когда же спектр станционной помехи относительно хорошо согласуется с полосой пропускания приемного тракта, то в модели учитывается закон модуляции мешающего сигнала посторонней радиостанции. В этом случае формирование выборок квадратур станционных помех производится точно так же, как и для сигнала. Для простоты считается, что приходящие от посторонних радиостанций мешающие сигналы имеют однолучевое распространение. Считается также, что число станционных помех, которые одновременно попадают в полосу пропускания тракта промежуточной частоты приемного устройства, подчиняется усеченному закону Пуассона. Распределение помех вдоль оси частот принимается равномерным, а закон распределения ширины полос частот спектра помех считается логнормальным. Распределение способов модуляции станционных помех задается в виде отдельного массива, из которого конкретная реализация метода модуляции выбирается по случайному закону.

Имея квадратурные отсчеты по отдельно взятым помехам, можно сформировать результирующие отсчеты квадратур в виде сумм индивидуальных отсчетов:

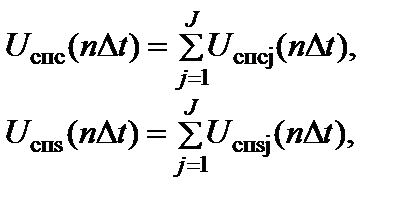(4.6.12)

где U _спcj(nDt) и U _спsj(nDt) - квадратурные отсчеты j -ой станционной помехи.

Имея отсчеты квадратур на выходе тракта промежуточной частоты приемного устройства, соответственно, для шумового компонента помех, станционных помех и многолучевого сигнала, легко сформировать отсчеты квадратур результирующего напряжения:

U _резc(n) = U _c(nDt) + U _шc(n) + U _спc(nDt), (4.6.13)

U _резs(n) = U _s(nDt) + U _шs(n) + U _спs(nDt).

При наличии в тракте РПУ нелинейных элементов требуется отсчеты суммы квадратур U _рез(n)= U _резc(n) + U _резs(n) функционально преобразовать в соответствии с ПХ НЭ с последующим определением значений квадратур результата преобразований методом дискретного преобразования Фурье. При этом необходимо увеличить в соответствующее число раз количество отсчетов сигнала на заданном интервале времени, например, длительности элемента сообщения, чтобы учесть влияние на конечный результат оценок квадратур сигнала наиболее значимых гармоник и интермодуляций сигнала и помех, которые появляются в результате их взаимодействия на ПХ НЭ.

 

4.7. Компьютерное имитационное моделирование трехмерного

пространственно-временного канала связи

Радиоволну, приходящую i -м лучом в точку приема, расположенную на значительном удалении от места ее излучения, можно считать плоской. В общем случае, она является эллиптически поляризованной [262] и может быть представлена в виде двух линейно поляризованных волн с взаимно перпендикулярными плоскостями поляризации [158]. Если на входе передающей антенны имеет место колебание u (t), то с учетом коэффициента направленности этой антенны и коэффициентов передачи m_ij среды распространения для
совокупности J -х компонентов i -го луча в точке приема можно записать выражения,

которые определяют напряженность электрического поля по азимутальной и меридиональной осям перпендикулярных вектору Пойтинга данного луча соответственно с ортами :

(4.7.1)

(4.7.2)

где m_aij и m_bij - модули коэффициентов передачи парциальных каналов,

D t _ij - время задержки соответствующих j -х компонентов i -го луча,

a_i и b_i - азимутальный и меридиональный углы прихода i -го луча,

J _i - число компонентов в i -ом луче, имеющих линейную поляризацию.

В случае узкополосного колебания

u (t) = U (t) cos(w t + y(t)) (4.7.3)

уравнения (4.7.1) можно записать в следующем виде:

(4.7.4)

С учетом того, что U (t) и y(t) медленно меняющиеся по сравнению с cos(w t) и w t величины, справедливы следующие выражения:

(4.7.5)

где D t _i - среднее время задержки радиоволны, приходящей i -м лучом.

Известно, что сумма гармонических колебаний с одинаковой частотой и различными амплитудами и фазами может быть представлена гармоническим колебанием с результирующими амплитудой и фазой [18]. Поэтому (4.7.5) можно
записать в виде:

(4.7.6)

Считая для простоты D t _i = 0, из первого уравнения находим:

; (4.7.7)

. (4.7.8)

Обозначив h_ai-h_bi = Q_i, преобразуем второе уравнение (4.7.6) к виду:

(4.7.9)

Избавляясь в этом уравнении от радикала, получим выражение

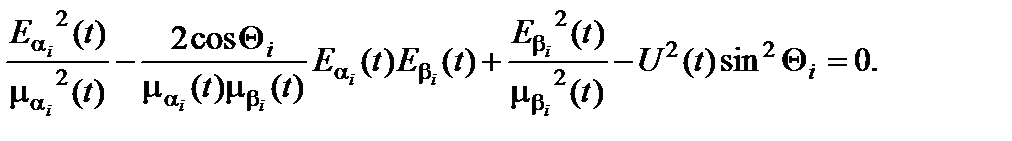(4.7.10)

Это уравнение кривой 2-го порядка с определителем

(4.7.11)

Главный минор этого определителя

(4.7.12)

что доказывает эллиптичность кривой, описываемой уравнением (4.7.9). Тем самым доказано, что суперпозиция J компонентов i -го луча с линейной поляризацией в общем случае является эллиптически поляризованной волной.

Пользуясь общими методами аналитической геометрии, находим угол наклона эллипса

. (4.7.13)

Большая и малая полуоси эллипса описываются выражениями:

, (4.7.14)

. (4.7.15)

Коэффициент эллиптичности равен

. (4.7.16)

Из этого выражения следует, что при Q_i = np К _э = 0, т. е. эллипс вырождается в прямую линию с углом наклона j_i:

. (4.7.17)

Это соответствует случаю линейной поляризации. При m_ai=0 или m_bi=0 поляризация также является линейной (азимутальной и меридиональной, соответственно). При Q_i = (2n + 1)p / 2 выражение (4.7.10) принимает канонический вид:

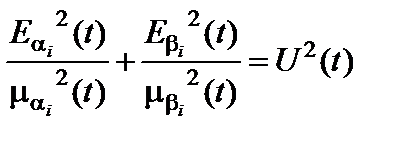(4.7.18)

и (4.7.19)

Если при этом m_ai(t) = m_bi(t), то выражение (4.7.18) превращается в уравнение окружности, а К _эi становится равным единице, что соответствует случаю круговой поляризации.

Когда выполняется условие 2pn < Q_i < (2n + 1)p, т. е. колебание Е _ai(t) отстает по фазе от колебания Е _bi(t), то конец вектора напряженности электрического поля вращается по часовой стрелке (поляризация левого вращения встречной волны). Когда же (2n - 1)p < Q_i < 2pn, т. е. колебание Е _ai(t) опережает по фазе колебание Е _bi(t), то конец вектора напряженности электрического поля вращается против часовой стрелки (поляризация правого вращения встречной волны) [89].

Таким образом, параметры m_ai, m_bi и Q_i полностью характеризуют вид поляризации радиоволны, приходящей i -м лучом. При этом коэффициенты передачи m_ai и m_bi обусловливают размеры прямоугольника, в который вписывается эллипс поляризации, и вместе с углом Q_i определяют параметры эллипса в соответствии с выражениями (4.7.12)¸(4.7.15).

Необходимо заметить, что в общем случае параметры m_ai и m_bi могут быть взаимно зависимыми величинами. Поэтому для более полной характеристики напряженности поля i-го луча необходимо знание оценок, как минимум, коэффициента их взаимной корреляции.

На рис. 4.7.1 изображены прямоугольник со сторонами 2m_a U и 2m_b U и вписанные в него эллипсы, которые соответствуют различным значениям угла q. На этом же рисунке стрелками показано направление вращения вектора напряженности электрического поля для положительных и отрицательных значений угла q.

При наличии одного луча и линейно поляризованных по ортам антенн параметры m_a и m_b этого луча нетрудно определить следующим образом:

(4.7.20)

где e_a(t) и e_b(t) - амплитуды ЭДС на выходах линейно поляризованных антенн.

Угол Q может быть измерен с помощью фазового детектора [307]:

, (4.7.21)

где U _фд - напряжение на выходе фазового детектора,

К _a и К _b - коэффициенты передачи трактов соответствующих приемных устройств.

mb U

Q<0 Q<0

Q>0 Q>0

ma U

Q=2np

(4n+1)p/2<Q<(4n+3)p/2

Q=(2n-1)p/2

2ma U

Q=(2n-1)p

(4n-1) p/2<Q<(4n+1) p/2

2mb U

 

 

 

 

Рис. 4.7.1. Зависимость формы эллипса поляризации от m_a, m_b и Q.

 

В общем случае параметр Q(t) является функцией времени.

Если канал связи является многолучевым, то определение параметров поляризации по отдельным лучам требует принятия особых мер, которые позволили бы выделить отдельные лучи (например, применения широкополосных сигналов, узконаправленных антенн и т. п.).

Таким образом, для моделирования отдельного i-го луча необходимо знать его углы прихода в точку приема a_i, b_i, время задержки Dt_i и статистические характеристики параметров m_ai(t), m_bi(t) и Q_i(t).

Из вышеизложенного следует, что, в случае линейно-поляризованной волны, можно считать ее состоящей из одного единственного компонента. Эллиптически поляризованная волна содержит не менее двух линейно поляризованных компонентов.

Так как для декаметрового канала связи характерна многолучевость, то результирующую напряженность электрического поля при наличии числа лучей равном I можно представить в следующем виде:

(4.7.22)

Таким образом, для моделирования результирующего трехмерного электромагнитного поля, представляющего собой суперпозицию I лучей, необходимо задавать N = 6× I характеристик для каждого i -го луча: a_i(t),, b_i(t), m_ai(t), m_bi(t), Q_i(t) и Dt_i.

Такого рода модель трехмерного КС дает возможность имитировать работу приемного центра с разнесенным приемом сигналов по поляризации, пространственно-разнесенный прием, прием с компенсацией станционных помех (пространственная фильтрация) и т. п. Рассмотрим для примера модель приема сигналов на две пространственно-разнесенные антенны.

4.8. Компьютерная имитационная модель КС для пространственно-

разнесенного приема радиосигналов

С целью повышения надежности связи в условиях замираний нашли широкое применение методы приема сигналов на разнесенные в пространстве антенны. Для моделирования такого рода систем необходимо знание напряженности электрического поля в любой точке заданного пространства.

Рассмотрим случай приема сигналов на антенны, разнесенные по поверхности, представляющей собой горизонтальную плоскость. Пусть заданы углы прихода лучей a_i(t) и b_i(t) и их параметры m_ai(t), m_bi(t) и Q_i(t), которые в общем случае изменяются случайным образом во времени. Зададим конкретные значения указанных величин в данный момент времени в точке с координатами х = 0 и у = 0, в которой может быть расположена приемная антенна, и определим напряженность поля Е _i00 в этой точке пространства для каждого луча i. Зададим какие-либо координаты х и у, отличные от координат первой точки пространства, в которой может быть расположена другая приемная антенна. Если известен закон изменения параметров канала связи, то напряженность поля в точке (х,у) описывается выражением:

(4.8.1)

где D Т _i - время задержки для напряженности поля, обусловленной i -м лучом.

(4.8.2)

Здесь с - скорость распространения радиоволны в свободном пространстве (скорость света).

Рассмотрим в качестве примера изображенный на рисунке 4.8.1 наиболее простой случай двухлучевого канала связи.

Поставим следующую задачу: для заданных параметров a₁, b₁, a₂, b₂ и частоты колебаний f Гц найти такие координаты для второй антенны, отнесенной в пространстве от первой, имеющей координаты х = 0 и у = 0, для которых будет справедливо равенство

Ф ₁(х,у) - Ф ₂(х,у) = ±p(2n+1), (4.8.3)

где Ф _i(х,у) = 2pfD T _i(x,y). (4.8.4)

Линии равной засветки

a2

a1

b1

b2

b01

a01

b02

a02

-Δy

3Δy

5Δy

-Δx

-3Δx

Δx

x

y

z

γ

 

 

 

Рис. 4.8.1. Линии равной засветки при двухлучевом канале связи

 

В этом случае при замирании сигнала на одной из антенн, на другой антенне происходит когерентное сложение лучей, т. е. выполняются наилучшие условия
разнесенного приема. Уравнение, которое удовлетворяет вышеуказанному условию, может быть получено из (4.8.2) с учетом (4.8.3) и (4.8.4):

(4.8.5)

Это выражение является уравнением семейства прямых, характеризующих линии равной “засветки”. Они смещены друг относительно друга вдоль оси у на величину, кратную 2D у, где

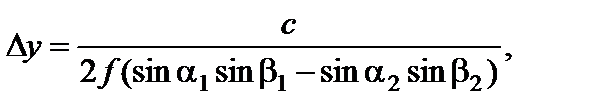(4.8.6)

и имеют угол крутизны g:

(4.8.7)

Семейство прямых пересекает ось х в точках с периодом 2D х, где

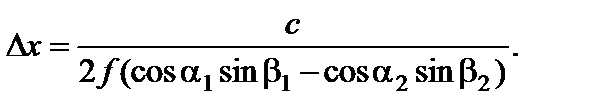(4.8.8)

Значения ±D у являются минимально допустимыми расстояниями вдоль оси у при х = 0, которые удовлетворяют поставленным условиям. Аналогично, значения ±D х - минимально допустимые расстояния вдоль оси х при у = 0. Если ось абсцисс х ориентирована навстречу приходящей радиоволне, то Dу характеризует расстояние при разнесении антенн поперек трассы, а Dх характеризует расстояние при разнесении антенн вдоль трассы.

В [97] показано, что поперечное разнесение требуется в среднем на порядок меньше продольного. В [61] указана другая относительная величина этих расстояний, равная двум. Воспользовавшись выражениями (5.7.6) и (5.7.8), произведем оценку расстояний между антеннами при поперечном и продольном разнесении для следующих конкретных значений параметров: b₁ = 80^о; b₂ = 85^о; a₁ = -a₂; l = 30м (f = 10МГц).

Результаты расчета приведены в таблице 5.7.1. В этой же таблице приведены значения углов g в градусах.

Из приведенной таблицы видно, что при конкретных заданных значениях параметров поперечное и продольное разнесение может отличаться относительно друг друга от трех до десяти и более раз, в зависимости от девиации азимутальных углов. При этом поперечное разнесение требует меньшего расстояния между антеннами, что хорошо согласуется с рекомендациями, данными в [61] и [97]. Однако поперечное разнесение очень критично к величине девиации азимутального угла. Если азимутальные углы прихода обоих лучей будут равными нулю, то поперечное разнесение становится не эффективным.

Интерференционная картина на плоскости имеет определенный узор. В нашем конкретном случае - это параллельные прямые, которые характеризуют местоположение равных фаз (равной “засветки” поверхности). Если разнесенные в пространстве антенны оказываются в местах равной “засветки”, то эффективность разнесенного приема сигналов уменьшается.

Зависимость величин D у,D х и g от азимутальных углов a1 и a2

a1 [гр] a2 [гр] D у [м] D у /l D х [м] D х /l g[гр]

-1 1 434 14,5 1318 43,9 18,23

-2 2 217 7,2 1318 43,9 9,35

-3 3 145 4,6 1319 44 6,26

-4 4 108 3,6 1320 44 4,7

-5 5 87 2,9 1322 44 3,76

-10 10 44 1,5 1335 44,5 1,87

Таблица 4.8.1.

 

 

Таким образом, зная количество лучей I, углы их прихода a_i и b_i, время задержки Dt_i, параметры поляризации m_ai, m_bi и Q_i каждого из лучей, можно с помощью выражений (4.7.5) и (4.7.21) определить напряженность электрического поля в любой точке пространства, на котором осуществляется прием сигнала.

Приняв эту точку за начало прямоугольной системы координат, можно с помощью выражений (4.8.1) и (4.8.2) определить напряженность электрического поля в любой другой точке, расположенной на плоскости. Если эти точки соответствуют месторасположению разнесенных в пространстве антенн, то, находя значения напряжения на выходе трактов предварительного усиления РПУ и заменяя континуальный сигнал дискретными отсчетами, можно получить компьютерную имитационную модель сигналов, принимаемых на пространственно-разнесенные антенны. Аналогичным образом формируются дискретные отсчеты для станционных помех. Отсчеты аддитивного шума на выходах разнесенных трактов можно формировать как независимые случайные процессы.

 

4.9. Компьютерная имитационная модель КС для компенсаторов помех

Компенсатор помех представляет собой в общем случае многотрактовое приемное устройство, которое имеет определенным образом распределенные в пространстве индивидуальные антенны. Для простоты в дальнейшем будем полагать, что все антенны имеют один и тот же тип поляризации. Сигналы на выходе ПЧ трактов РПУ суммируются с начальными фазами, которые могут варьироваться по заданному закону, зависящему от азимутального угла прихода помех. Если сигнал и помехи приходят в точку приема из разных направлений, то диаграмма направленности приемного комплекса может быть сформирована таким образом, что ее нули будут соответствовать направлениям прихода помех, в то время, как в направлении сигнала диаграмма направленности будет иметь коэффициент передачи отличный от нуля.

Каждый отдельный тракт приема ничем, в принципе, не отличается от обычного приемного тракта. Поэтому результаты, изложенные во всех предыдущих разделах по формированию отсчетов квадратур сигнала, могут быть полностью использованы и при формировании выборок квадратур для компенсатора помех с той лишь разницей, что колебания на выходе индивидуальных трактов будут отличаться фазами, которые обусловлены азимутальными углами прихода сигналов. Для простоты будем считать, что шумовые компоненты на выходах
индивидуальных приемных трактов являются независимыми случайными величинами. В дальнейшем для конкретности общее число индивидуальных приемных трактов примем равным четырем.

Решим задачу формирования отсчетов квадратур сигнала и станционных помех на выходе трактов промежуточной частоты приемных устройств для четырехканального компенсатора помех.

Определим местоположение одной из имеющихся антенн полюсом полярной системы координат на поверхности Земли в точке приема сигнала. Присвоим этой антенне обозначение А ₀. Расстояние от антенны А ₀ до любой другой (k-ой) антенны обозначим L _k. Выберем любую из оставшихся трех антенн и обозначим ее А ₁. Через местоположения антенн А ₀ и А ₁ проведем линию, определив ее как полярную ось. Оставшимся двум антеннам присвоим произвольно обозначения А ₂ и А ₃. В этом случае антенны будут иметь координаты, соответствующие таблице 4.9.1.

Антенна Радиус Полярный угол А 0 0 0 А 1 L 1 0 А 2 L 2 a2 А 3 L 3 a3

Таблица 4.9.1.

 

Отличные от нуля параметры L _k и a_k задаются оператором в качестве входных данных модели.

Пусть сигнал (станционная помеха) приходит в точку приема лучом, проекция которого имеет полярный угол b. В этом случае проекция радиуса L _k на направление проекции луча прихода сигнала (станционной помехи) будет равна

L _kc = L _kcos(b - a_k). (4.9.1)

Разность фаз на выходах каналов связи, которые соответствуют антеннам А ₀ и А _k, будет равна

D Ф _k = { L _kc/l }2p, (4.9.2)

где { X } - дробная часть числа Х,

l- длина радиоволны, которая вычисляется по формуле:
l= с / f. (4.9.3)

Здесь f - частота сигнала в Гц, с - скорость распространения света в свободном пространстве.

Углы прихода сигнала и станционных помех принимаются распределенными равномерно в пределах 2p. Зная величины D Ф _k для каждой антенны, можно сформировать отсчеты квадратур для сигналов и станционных помех на выходе соответствующих индивидуальных трактов. Определим тракт с антенной А ₀ как основной. Будем считать, что начальные фазы сигнала и помех, обусловленные углами прихода, на выходе этого тракта равны нулю, и отсчет комплексной амплитуды сигнала (станционной помехи) в этом случае описывается выражением:

U ₀(nDt) = A (nDt) exp(j Ф ₀(nDt)), (4.9.4)

где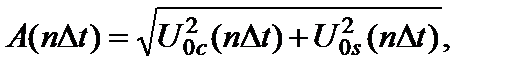

Ф ₀(nDt) = arctg(U _0s(nDt)/ U _0c(nDt)) для U _0c(nDt) > 0,

Ф ₀(nDt) = arctg(U _0s(nDt)/ U _0c(nDt)) + p для U _0c(nDt) < 0,

U _0c(nDt) и U _0s(nDt) - отсчеты квадратур сигнала (станционной помехи) на выходе тракта промежуточной частоты приемного устройства, которое работает с основной антенной.

На выходе тракта промежуточной частоты K -го приемного устройства, которое работает с А _k-ой антенной, отсчеты комплексной амплитуды соответствующего колебания будут описываться выражением:

U _k (nDt) = A (nDt) exp(j[ Ф ₀(nDt)+ D Ф _k]). (4.9.5)

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: