Основные положения, выносимые на защиту 9 глава
Рис. 2.10.4. Амплитудные характеристики идеального и условно идеальных преобразователей частоты.
1-модель № 1; 2-модель № 2; 3-идеальный преобразователь (U г = b/2)
На рисунке 2.10.5 приведены характеристики блокирования моделей. Первая модель не позволяет превышать совокупностью входных воздействий границу заданного интервала [- b, b ]. Вторая модель мало отличается от идеального преобразователя даже при значительных превышениях уровнями входного воздействия заданных границ.
Рис. 2.10.5. Характеристики блокирования преобразователей.
1 - модель № 1; 2 - модель №2; 3 - идеальный преобразователь (U г= b /2)
На рисунке 2.10.6 приведены рассчитанные значения амплитуд интермодуляционных составляющих третьего порядка. Первая модель дает резкое увеличение роста амплитуд этого вида интермодуляций при превышении входным воздействием допустимых границ. Вторая модель более соответствует реальным условиям с плавным нарастанием уровня интермодуляции третьего порядка при увеличении уровней входного воздействия.
Таким образом, по всем практически важным параметрам необходимо отдать предпочтение второй модели ограниченно-идеального преобразователя. Однако обе описанные модели одинаково крайне важны как полигоны, позволившие произвести апробацию предлагаемого метода при заранее известных результатах с оценкой скорости сходимости к ним в зависимости от числа членов в аппроксимирующем ряде Фурье. Такого рода проверка, результаты которой приведены выше, показала
эффективность представления заранее известной ПХ преобразователя частоты в виде ряда Фурье. Полученные результаты показали целесообразность представления ПХ таким образом, чтобы за пределами допустимого уровня входных воздействий избегать ее резких изломов, что позволяет сократить время вычислений.
Рис. 2.10.6. Уровни интермодуляционных спектральных составляющих 3-го порядка на выходе преобразователей частоты.
1 - модель № 1; 2 - модель №2; 3 - идеальный преобразователь (U г= b /2)
2.11. Имитационно-аналитическое моделирование трассовых
испытаний РПУ
Имитационно-аналитическая модель трассовых испытаний РПУ учитывает всю совокупность аддитивных помех, которые попадают в полосу пропускания его ФПИ, и их взаимодействие на НЭ усилительного тракта как с сигналом, так и между собой. Если известна вероятность поражения канала связи станционной помехой, то их общее число Мi в i-м сеансе в заданной полосе Δ f фильтра предварительной избирательности находится по закону Пуассона. Уровень j-й помехи U пj определяется из предположения, что уровни станционных помех распределены по логарифмически-нормальному закону. Уровни сигналов в различных сеансах связи также считаются распределенными по логарифмически-нормальному закону. Законы замирания сигнала и помех принимаются релеевскими, райсовскими, односторонне-нормальными и др. с учетом статистики приведенной, например, в
[301]. Предполагается, что вдоль оси частот в пределах полосы пропускания фильтра предварительной избирательности станционные помехи распределены равномерно. В этом случае, с учетом формулы (2.3.2), уровень сигнала U с(вых)(t) на выходе УТ РПУ описывается выражением
 . (2.11.1)
. (2.11.1)
Уровень атмосферного шума, преобразованного на выход УТ РПУ, определяется с помощью следующего выражения:
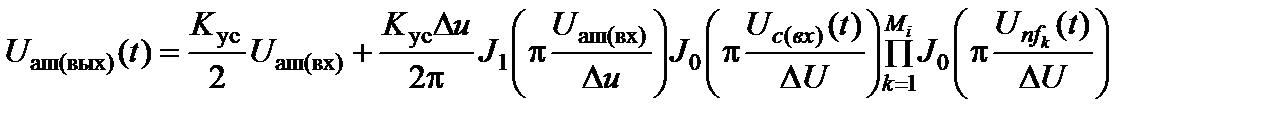 . (2.11.2)
. (2.11.2)
Уровни станционных помех  , частоты которых совпадают с частотой сигнала, определяются аналогичным образом:
, частоты которых совпадают с частотой сигнала, определяются аналогичным образом:
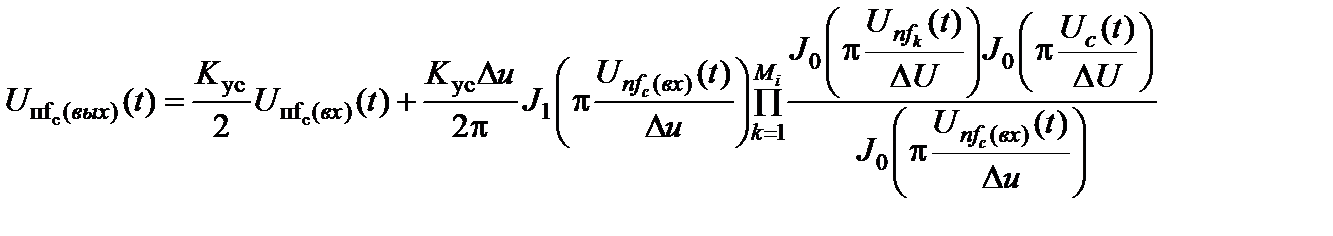 . (2.11.3)
. (2.11.3)
Одновременно на выходе УТ РПУ за счет взаимодействия станционных помех образуются интермодуляционные помехи нечетных порядков, часть из которых при выполнении условий (2 f r - f p) = f c, (f r + f p - f s) = f c, 3 f r - 2 f p= f c и т. д. попадает в ФОИ. Уровни наиболее значимых интермодуляционных помех третьего порядка определяются следующим образом:
 , (2.11.4)
, (2.11.4)
 . (2.11.5)
. (2.11.5)
Определив уровни сигнала, атмосферного шума, попавших на частоту сигнала станционных помех, и все уровни интермодуляционных помех, которые попадают в полосу пропускания ФОИ, можно найти общую мощность всех аддитивных помех как сумму их индивидуальных мощностей и рассчитать отношение сигнал/помеха H2. Зная H2, можно определить вероятность ошибочного приема элемента в любой заданный момент времени, построить вектор ошибок и определить число этих ошибок, обусловливающих качество сообщения, принятого в проводимом сеансе связи. Для коротких сеансов связи, когда длительность сообщения во много раз меньше интервала корреляции замирания сигнала и помех, оценку качества сеансов связи можно производить непосредственно по отношению сигнал/помеха H2.
2.12. Основные результаты второй главы
Во второй главе рассмотрен метод моделирования ГТ КВ РПУ и входящих в его состав нелинейных безынерционных элементов. Этот метод отличается тем, что нелинейные проходные характеристики ГТ и нелинейных элементов описываются комбинированными функциями, которые, в общем случае, являются многочленами, состоящими из степенных, показательных и тригонометрических рядов (2.1.1). Этот метод позволяет при относительной простоте математических выражений в аналитических моделях нелинейных каналов связи снять ограничения на уровень входных воздействий, а также на порядок и, соответственно, на количество гармоник и интермодуляционных компонентов выходного колебания. Предложенный метод существенно упрощает анализ явлений, которые происходят при полигармоническом входном воздействии (2.3.1) в трактах, содержащих различного рода нелинейные элементы. Из общих выражений (2.2.1) и (2.2.2) следуют всевозможные частные случаи типовых моделей.
Предложенная двухпараметрическая модель усилительного каскада (2.2.2) является относительно простой, но, тем не менее, она отражает все наиболее важные явления, которые характерны для нелинейных усилителей. Из общего аналитического выражения (2.3.2), описывающего колебание на выходе усилительного тракта при полигармоническом входном воздействии, получены
выражения для амплитудной характеристики, характеристики блокирования, уровней интермодуляционных колебаний.
Произведенные с помощью указанной модели аналитические расчеты полностью совпали с результатами имитационного моделирования.
В работе предложена методика определения параметров модели по основным характеристикам усилительного тракта, таким, как коэффициент усиления и динамический диапазон. Приведенная таблица 2.3.1 зависимости параметра модели D U от динамического диапазона усилительного тракта позволяет легко производить синтез ПХ вида (2.2.2). Произведена аппроксимация ПХ ГТ РПУ вида u 2 = arctg(u 1) комбинированной функцией, представляющей собой сумму линейной и синусоидальной функций, и показано, что на рабочем участке характеристики основные характеристики ГТ обеих моделей отличаются не более, чем на 1 %.
На ряде конкретных примеров продемонстрированы возможности предложенной модели при анализе многокаскадных усилительных трактов. С помощью полученных рекуррентных уравнений (2.5.2) и (2.5.3) произведен расчет различных характеристик многокаскадного тракта. Исследована зависимость потерь динамического диапазона многокаскадного тракта от числа содержащихся в нем усилительных каскадов. Найдено аналитическое выражение (2.5.10), которое удовлетворительно аппроксимирует эту зависимость и может быть рекомендовано для использования в инженерной практике.
В главе описана разработанная общая аналитическая модель усилителя-ограничителя (2.8.4), основанная на представлении его ПХ совокупностью линейной функции и ряда Фурье. Получены аналитические выражения для всех основных характеристик УО. Сравнение с результатами, полученными на модели Берга при моногармоническом входном воздействии и посредством гармонического анализа при равноуровневом бигармоническом входном воздействии на идеальный ограничитель, показали полное совпадение этих результатов с вновь полученными. В отличие от известных моделей усилителя-ограничителя, разработанная модель не накладывает каких-либо ограничений на количество и уровень входных воздействий и, с этой точки зрения, является наиболее универсальной.
Во второй главе рассмотрены различные аналитические модели преобразователей частоты, которые являются неотъемлемой частью любого усилительного тракта РПУ, и, поскольку в идеальном виде (2.8.2) практически реализованы быть не могут, то заведомо являются сугубо нелинейными его элементами. Для моделирования преобразователей частоты использован тот же метод, что и для моделирования нелинейных усилителей - аппроксимация ПХ нелинейных элементов комбинированными функциями, которые, в общем случае, являются многочленами, состоящими из степенных, показательных и тригонометрических рядов.
Рассмотрен простой вариант идеального преобразователя (2.8.2) и более сложные типовые модели преобразователя частоты (2.8.4 и 2.8.17). Модель идеального преобразователя адекватна реальному устройству лишь в отношении коэффициента передачи сигнала в процессе преобразования частоты, причем при относительно малых уровнях входных воздействий. Модель (2.8.4) является адекватной также и в отношении динамического диапазона. Обобщенная модель (2.8.17) дополнительно адекватна и в отношении заданного значения блокирования малого сигнала большим.
С помощью полученных в работе выражений (2.9.8)¸(2.9.10) и (2.9.16)¸(2.9.18) можно определять параметры предложенных математических моделей по параметрам реальных преобразователей частоты. Для синтеза модели (2.8.4) необходимо задавать коэффициент передачи и динамический диапазон преобразователя частоты, а для синтеза модели (2.8.17) необходимо дополнительно задавать координаты какой-либо из точек на его характеристике блокирования. Приведенная таблица 2.9.1 дает возможность определять параметры модели (2.8.4) по заданному динамическому диапазону преобразователя и его коэффициенту усиления.
Предложенный в работе метод представления ПХ преобразователя частоты тригонометрическими многочленами апробирован на двух моделях ограниченно-идеального преобразователя, когда его ПХ на ограниченном отрезке оси абсцисс аппроксимируется рядом Фурье. Из результатов исследования видно, что модель
ограниченно-идеального преобразователя (2.10.22) имеет характеристики, которые качественно соответствуют характеристикам реальных преобразователей частоты с большим динамическим диапазоном. С учетом этого, модель (2.10.22) может быть рекомендована для практического использования в отдельных частных случаях для каналов с большим (но не бесконечным) динамическим диапазоном и слабо выраженным явлением блокирования.
Подводя итоги исследования математических моделей каналов с преобразованием частоты, можно сделать вывод о целесообразности использования в общем случае типовой модели (2.8.17). Если нет необходимости учитывать характер блокирования, а достаточно учета лишь динамического диапазона, то можно ограничиться относительно простой моделью (2.8.4). В отдельных случаях каналов с большим динамическим диапазоном может быть использована модель ограниченно- идеального преобразователя (2.10.22).
Большое значение для практики представляет разработанный метод имитационно-аналитического моделирования сравнительных трассовых испытаний РПУ, имеющих различные характеристики. Благодаря аппроксимации ПХ НЭ комбинированными функциями, этот метод позволяет определять отношение сигнал/помеха на выходе ФОИ РПУ при любом числе станционных помех, попадающих в полосу пропускания ФПИ РПУ. Имитационно-аналитический метод моделирования сравнительных трассовых испытаний РПУ позволяет находить зависимость КИД КС с различными РПУ, определять зависимости КИД от мощности передатчика (и других параметров КС) и, в конечном итоге, производить оценку энергетического выигрыша (проигрыша) одного КС по отношению к другому в условиях, мало чем отличающихся от реальных.
В качестве побочных результатов, которые могут иметь самостоятельное значение в отдельно взятых физико-математических приложениях, следует указать на полученные в работе следующие ряды бесселевых функций, пределы которых удалось определить: (2.8.12), (2.8.20), (2.8.34), (2.8.35), (2.8.39), (2.8.42), (2.8.44)¸(2.8.49), (2.10.5)¸(2.10.13), (2.10.17), (2.10.18), (2.10.23)¸(2.10.32).
Предложенная автором диссертации методика моделирования нелинейных усилительных трактов была положена в основу системы моделирования магистральных радиоприемных устройств “Омь-1” [4, 128]. С помощью разработанных моделей получен ряд важных результатов по исследованию влияния параметров радиоприемных устройств на помехоустойчивость приема сообщений [129, 147, 197, 198]. С использованием системы моделирования “Омь-1” в Омском НИИ приборостроения проведены ряд НИР и ОКР, касающиеся магистральных КВ радиоприемных устройств 4-го и 5-го поколений.
3. МЕТОДЫ АНАЛИТИЧЕСКОГО МОДЕЛИРОВАНИЯ ЦИФРОВЫХ РПУ
3.1. Задачи и методы моделирования цифровых РПУ
Методы цифровой обработки сигналов в настоящее время широко используются при приеме дискретных сообщений [27, 133, 141 и др.]. Основным элементом устройств цифровой обработки является аналого-цифровой преобразователь (АЦП), который выполняет две функции: квантования по уровню и дискретизации по времени. Вопросы дискретизации по времени в настоящее время изучены достаточно глубоко и широко освещены как в учебной [12, 60, 205 и др.], так и в научно-технической литературе [9, 133, 141 и др.] Что касается явлений, происходящих при квантовании сигналов по уровню, то они все еще нуждаются в дальнейшем изучении. Объясняется это трудностями аналитического анализа происходящих в квантователе явлений. Как правило, исследователи нелинейных явлений, имеющих место при квантовании сигналов, ограничиваются рассмотрением стохастической модели, позволяющей оценить влияние шумов квантования на отношение сигнал/помеха [27, 133, 141 и др.]. Однако, при проектировании цифровых РПУ требуется определение их традиционных характеристик, например, определение амплитудной характеристики, характеристики блокирования (взаимной модуляции), интермодуляционной характеристики и т. п. В принципе, все эти характеристики можно получить с помощью имитационных моделей квантователя. Однако, в этом случае невозможно произвести аналитический анализ влияния отдельных параметров квантователя на характеристики канала связи. Поэтому целесообразно разрабатывать детерминированные аналитические модели квантователей, которые позволяют непосредственно определять заданные характеристики цифровых РПУ. Однако, учитывая то, что имитационные модели квантователя мало чем отличаются от реальных устройств, их целесообразно использовать в качестве полигонов, позволяющих оценить адекватность аналитических моделей.
Каждый из вышеперечисленных методов моделирования квантователей (стохастический, имитационный и детерминированный аналитический) имеет свои задачи, определенные достоинства и недостатки при их решении.
В данной главе основное внимание уделено разработке детерминированных аналитических моделей квантователя, сведения о которых в научно-технической литературе практически отсутствуют.
3.2. Моделирование идеальных квантователей
кусочно-линейными функциями
Передаточная характеристика квантователя имеет ступенчатый характер. Идеальный квантователь имеет бесконечно большое число шагов квантования и поэтому не меняет режима работы при сколь угодно больших уровнях входного воздействия. Математически для идеального квантователя с округлением ПХ можно представить в виде
 (3.2.1)
(3.2.1)
а для идеального квантователя с усечением - в виде
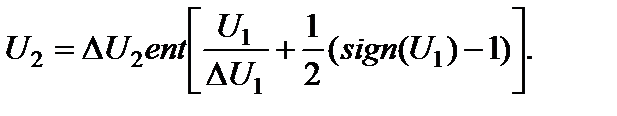 (3.2.2)
(3.2.2)
Выражения (3.2.1) и (3.2.2) можно записать в общем виде
 , (3.2.3)
, (3.2.3)
где a = 0 для квантователя с округлением,
a = 1 для квантователя с усечением.
В выражениях (3.2.1)¸(3.2.3) обозначено:
D U 1 - шаг квантования по входу,
D U 2 - шаг квантования по выходу.
Данная модель квантователя может быть использована как при имитационном, так и при аналитическом моделировании с моногармоническим входным воздействием [91]. На рис. 3.2.1 показаны компоненты колебаний на выходе
квантователя с округлением при моногармоническом входном воздействии. Каждый из компонентов представляет собой биполярное периодическое колебание. Определяя амплитуды спектральных составляющих этих колебаний и производя суммирование тех значений, которые соответствуют одним и тем же частотам, можно определить значения амплитуд всех гармоник квантованного колебания.
Для разложения в ряд Фурье периодических колебаний, изображенных на рисунке 3.2.1, необходимо знать углы jn, которые определяют моменты достижения входным колебанием n-го порога квантования. Значения jn могут быть определены по формуле:
| -4 -3 -2 -1 0 1 2 3 4 U 1/∆ U 1
|
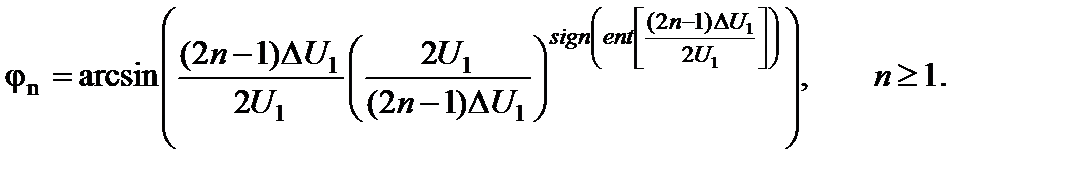
(3.2.4)
Рис. 3.2.1. Компоненты квантованного моногармонического колебания
При U 1 < (D U 1/2)(2n-1) jn = p/2, что соответствует отсутствию n-го компонента на выходе квантователя.
Амплитуда (2m-1)-ой гармоники n-го компонента может быть записана с учетом соответствующих коэффициентов ряда Фурье [18] в виде
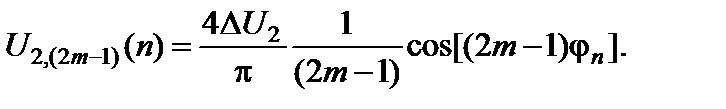 (3.2.5)
(3.2.5)
В результате имеем следующее выражение для (2m-1)-ой гармоники выходного колебания квантователя, на который воздействует гармоническое колебание:
 (3.2.6)
(3.2.6)
Выражение (3.2.6) дает возможность получить точное значение амплитуды любой гармоники колебания на выходе квантователя с округлением.
Для квантователя с усечением при гармоническом входном воздействии jо всегда равно нулю, а нулевой компонент имеет обязательно отрицательную или положительную полярность. Для jn при n ³ 1 справедливо уравнение:
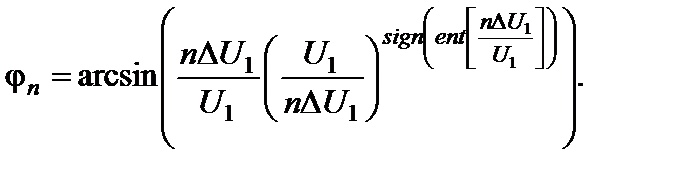 (3.2.7)
(3.2.7)
Уравнение (3.2.5) в этом случае остается справедливым. С учетом этого, можно получить выражение для (2m-1)-ой гармоники колебания на выходе квантователя:
 (3.2.8)
(3.2.8)
На рисунке 3.2.2 изображены амплитудные характеристики квантователя с округлением (кривая (1)) и с усечением (кривая (2)).
На рисунке 3.2.3 приведены зависимости амплитуд гармоник третьего порядка от уровня входного воздействия для квантователя с округлением (кривая (1)) и с усечением (кривая (2)).
Из рисунков видно существенное различие поведения характеристик лишь в начале координат. С превышением входным воздействием уровня, равного шагу квантования, характеристики имеют одинаковый характер поведения и отличаются сдвигом по фазе на половину шага квантования.
Рис. 3.2.2. Амплитудные характеристики квантователей:
(1) - с округлением, (2) - с усечением.
Результаты имитационного моделирования: (·) - с округл., (Ä) - с усеч.
Рис. 3.2.3. Зависимость амплитуд гармоник третьего порядка от уровня воздействия на вход квантователей:
(1) - с округлением, (2) - с усечением.
Результаты имитационного моделирования: (·) - с округл., (Ä) - с усеч.
(Примечание: отрицательным значениям амплитуды соответствует начальная фаза гармоники 1800)
Данная модель может быть использована для оценки точности расчетов, которые проводятся другими методами.
С целью оценки адекватности моделей может быть использована и имитационная модель с проходной характеристикой (3.2.3). Точность вычислительных экспериментов, проводимых с помощью этой модели, зависит от числа взятых выборок на заданном интервале времени. На рисунках 3.2.2 и 3.2.3 точками и крестиками нанесены результаты, полученные с помощью имитационного моделирования соответственно для квантователей с округлением и с усечением. Количество отсчетов на периоде в имитационной модели при определении амплитудной характеристики было взято равным 50, что позволило учитывать 25 гармоник, а при определении третьей гармоники, соответственно, 500, что позволило учитывать 250 гармоник.
Воспользуйтесь поиском по сайту:


 . (2.11.1)
. (2.11.1)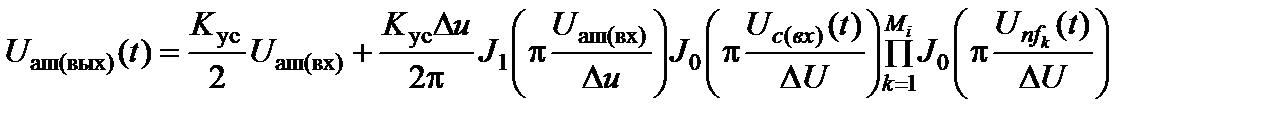 . (2.11.2)
. (2.11.2) , частоты которых совпадают с частотой сигнала, определяются аналогичным образом:
, частоты которых совпадают с частотой сигнала, определяются аналогичным образом: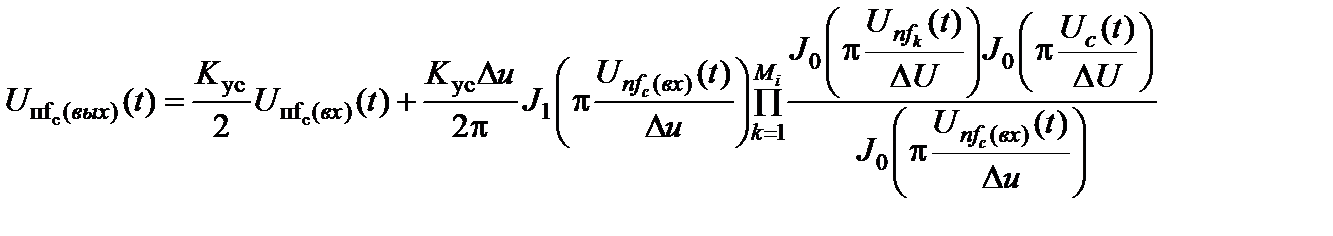 . (2.11.3)
. (2.11.3) , (2.11.4)
, (2.11.4) . (2.11.5)
. (2.11.5) (3.2.1)
(3.2.1)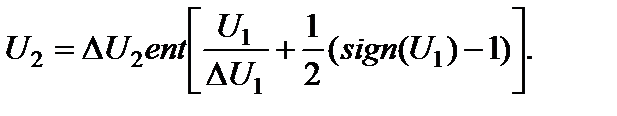 (3.2.2)
(3.2.2) , (3.2.3)
, (3.2.3)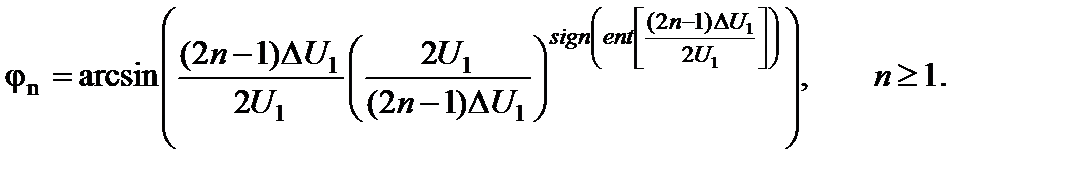 (3.2.4)
(3.2.4)
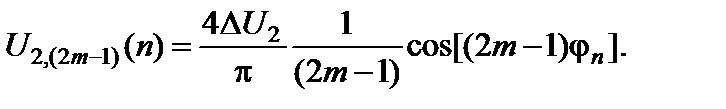 (3.2.5)
(3.2.5) (3.2.6)
(3.2.6)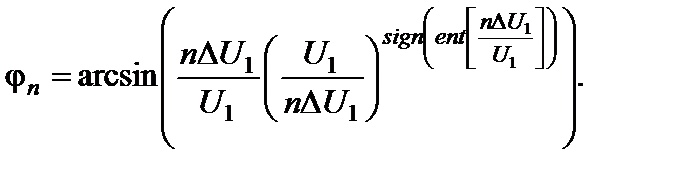 (3.2.7)
(3.2.7) (3.2.8)
(3.2.8)

