 |
Основные положения, выносимые на защиту 8 глава
|
|
|
|
Воспользовавшись свойством четных и нечетных функций, перепишем (2.7.5) в виде
U 2(t) = Fч1(U г(t) + U 1(t)) - Fч2(U г(t) - U 1(t)) +
+ Fч4(U г(t) + U 1(t)) - Fч3(U г(t) - U 1(t)) + (2.7.6)
+ Fн1(U г(t) + U 1(t)) - Fн4(U г(t) + U 1(t)) –
- Fн2(U г(t) - U 1(t)) + Fн3(U г(t) - U 1(t)).
Из (2.7.6) следует, что при одинаковых ПХ НЭ продукты преобразования, обусловленные нечетными частями характеристик, взаимно компенсируются, а результирующий алгоритм кольцевого смесителя с симметричной ПХ можно описать выражением
U 2(t) = FS1(U г(t) + U 1(t)) - FS2(U г(t) - U 1(t)), (2.7.7)
где FS1(х) и FS2(х) - четные функции.
Алгоритм (2.7.6) отдает предпочтение составляющим спектра выходного колебания, которые являются результатом взаимодействия нечетных гармоник входного колебания и колебания гетеродина.
Частотные номограммы колебаний, которые попадают в полосу фильтра промежуточной частоты, включенного на выходе простого, балансного и кольцевого
преобразователей, изображены, соответственно, на рисунках П-2.1, П-2.2 и П-2.3 в приложении 2. Из приведенных номограмм видно, что для всех типов преобразователей существуют две области частот входных колебаний, которые преобразуются к одной промежуточной частоте. Одна область частот - это область полезного сигнала, а другая - зеркальной помехи. Обычно зеркальные помехи подавляются с помощью селективных цепей, которые включаются на входе преобразователя. При недостаточном подавлении побочные (зеркальные) каналы могут оказывать существенное влияние на помехоустойчивость приема дискретных сообщений [20]. Однако имеется возможность дополнительной компенсации зеркальных помех на выходе преобразователя [206]. Это достигается использованием двух смесителей частоты и двух фазовращателей на угол 90 градусов. Соответствующий алгоритм такого преобразователя можно записать в виде
|
|
|
U 2(t) = U 21(t) + 
22(t), (2.7.8)
где U 21(t) = F11(U г(t) + U 1(t)) - F21(U г(t) - U 1(t)), (2.7.9)
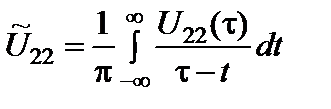- колебание, сопряженное по Гильберту колебанию U 22(t).
U 22(t) = F12(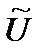
г(t) + U 1(t)) - F22(
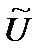г(t) - U 1(t)), (2.7.10)
где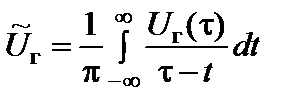 
- колебание, сопряженное по Гильберту колебанию U г(t).
Схема такого рода преобразователя и соответствующая номограмма для случая f г > f пч изображены на рисунке П-2.4 приложения 2.
Из приведенных в приложении 2 номограмм видно, что число не подавленных на выходе балансного смесителя интермодуляционных составляющих спектра
выходного колебания уменьшается в два раза по сравнению с простой схемой, не обеспечивающей какой-либо компенсации. Число не подавленных интермодуляционных составляющих на выходе кольцевого смесителя соответственно меньше в четыре раза, а на выходе схемы с дополнительной компенсацией зеркальных помех - в восемь раз.
На практике наиболее широкое распространение получили относительно простые схемы кольцевых смесителей, алгоритм функционирования которых описывается выражением (2.7.7). Поэтому в дальнейшем при моделировании каналов связи с преобразованием частоты будем считать, что в приемных трактах для преобразования частот используются такого рода смесители.
2.8. Типовые аналитические модели преобразователей частоты
Если функции FS1(x) и FS2(x) в модели кольцевого смесителя являются квадратичными параболами
FS1(x) = FS2(x) = a x 2, (2.8.1)
то такого рода смеситель является идеальным перемножителем, выходное колебание U2(t) которого описывается уравнением
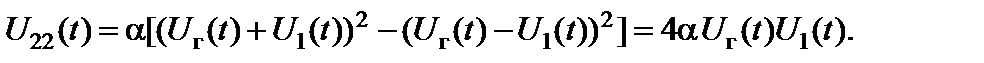(2.8.2)
Коэффициент передачи этого преобразователя частоты К зависит как от параметра a, так и от уровня колебания гетеродина U г:
K = 4a U г. (2.8.3)
Такая модель идеального преобразователя частоты может быть использована при малоуровневых входных воздействиях, когда допустимо считать анализируемый тракт исключительно линейным [51].
|
|
|
Другой несколько более сложной моделью является модель вида
, (2.8.4)
где параметр Du, как и в модели усилительного каскада (2.2.2), обеспечивает заданный уровень динамического диапазона преобразователя частоты. Очевидно,
что при малоуровневом входном воздействии, когда выполняются неравенства U г(t) << D u, U 1(t) << D u и
b1 = b2 = 4a, эта модель сходится к модели (2.8.2).
Представим (2.8.4) в виде
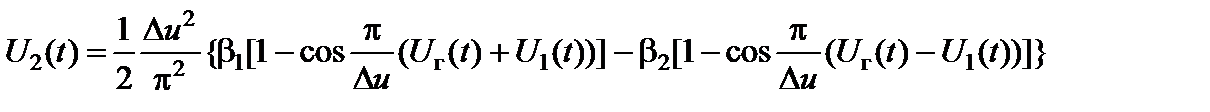. (2.8.5)
Функция вида
F(x) = 1 - cos(x), (2.8.6)
которая является математической моделью полуветви преобразователя частоты, изображена на рис. 2.8.1. Из рисунка видно, что при –π < x < π эта характеристика является четной функцией с монотонно возрастающими “крыльями”. В области малых значений аргумента эта функция может быть аппроксимирована параболой
F(x) =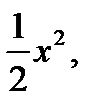 
(2.8.7)
которая также изображена на рис. 2.8.1.
| x2 / 2 |
| 1-cos(x) |
| U2 U2max |
| 1,0 |
| 0,5 |
| -3π/2 -π -π/2 0 π/2 π U1/∆u |
Рис. 2.8.1. Представление ПХ полуветви преобразователя частоты функцией
вида F(x)=1-cos(x).
При полигармонических входных воздействиях
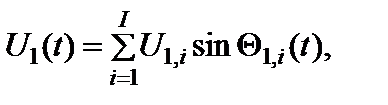(2.8.8)
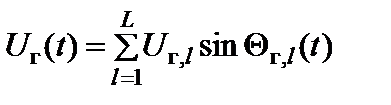(2.8.9)
напряжение на выходе преобразователя частоты описывается выражением
(2.8.10)
На выход фильтра промежуточной частоты (ФПЧ), включенный после преобразователя, проходят лишь те составляющие спектра выходного колебания, которые соответствуют неравенству
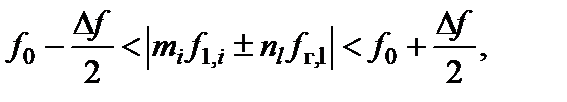(2.8.11)
где D f - полоса пропускания ФПЧ.
Остальные составляющие спектра существенно ослабляются в соответствии с амплитудно-частотной характеристикой ФПЧ.
Из выражения (2.8.10) можно получить все основные характеристики преобразователя. Например, при моногармоническом входном воздействии амплитудная характеристика описывается выражением
(2.8.12)
Соответственно коэффициент передачи преобразователя частоты при
U 1 << D u равен
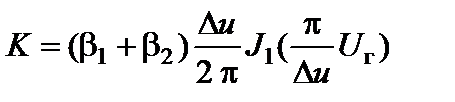. (2.8.13)
Из этого выражения следует, что коэффициент передачи имеет экстремум при p U г/D u = 1.8. В дальнейшем будем считать, что это условие выполняется.
При бигармоническом разноуровневом входном воздействии выражение для амплитуды блокируемого сигнала выглядит следующим образом:
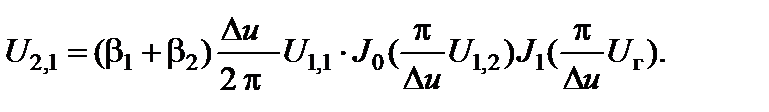(2.8.14)
|
|
|
Соответственно, характеристика блокирования описывается уравнением:
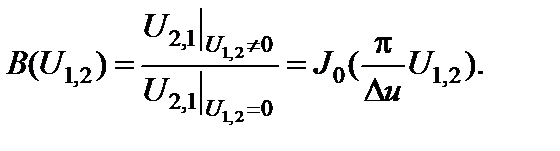(2.8.15)
При бигармоническом равноуровневом воздействии амплитуда интермодуляционного колебания третьего порядка равна
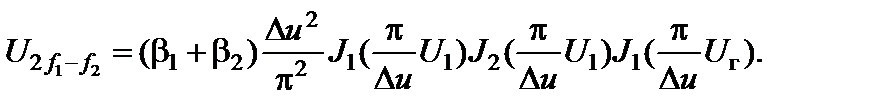(2.8.16)
Таким образом, зная параметры b1, b2 и Du, можно произвести аппроксимацию передаточной характеристики преобразователя частоты.
На рис. 2.8.2¸2.8.4 изображены, соответственно, амплитудная характеристика, характеристика блокирования и амплитудная характеристика интермодуляционной составляющей 3-го порядка преобразователя с ПХ вида (2.8.4).
| U 2 К∆ u |
| 0,5 |
| 0,25 |
| 0 0,25 0,5 U 1/∆ u |
| 1-cos(x) |
| x2/2 |
Рис. 2.8.2. Амплитудная характеристика преобразователя частоты
Расширить возможности аналитической модели позволяет изложенная ранее концепция представления ПХ преобразователя совокупностью степенных и тригонометрических функций вида
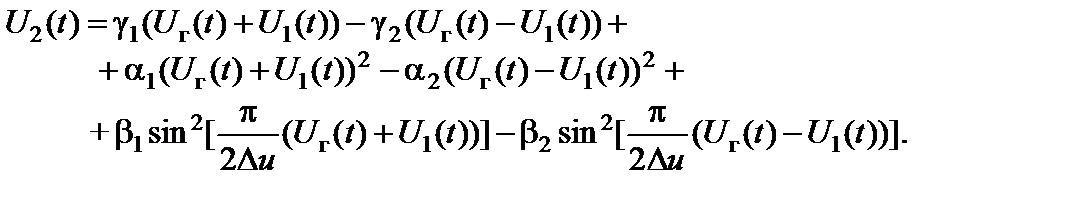(2.8.17)
Для простоты сначала ограничимся рассмотрением случая симметричной ПХ, когда g1 = g2 = 0, a1 = a2 = a, b1 = b2 = b. Колебание на выходе такого преобразователя частоты при полигармоническом входном воздействии описывается следующим выражением:
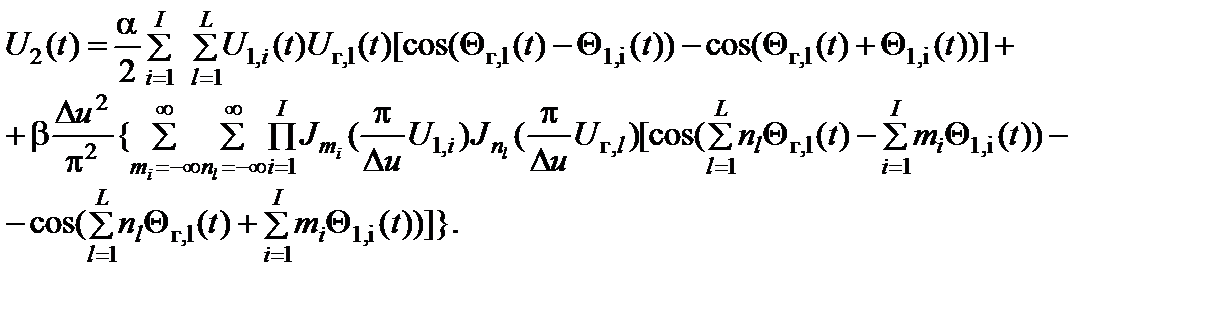(2.8.18)
Из этого выражения следуют все основные характеристики преобразователя.
Амплитудная характеристика:
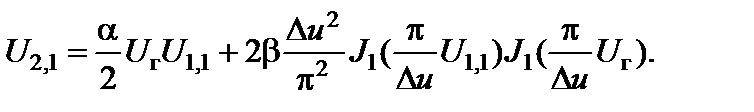(2.8.19)
Коэффициент усиления:
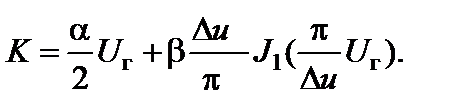(2.8.20)
Амплитуда блокируемого сигнала при разноуровневом бигармоническом входном воздействии:
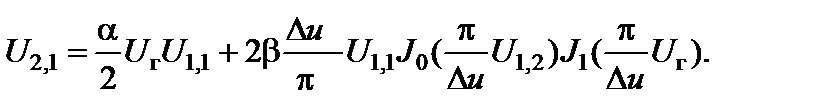(2.8.21)
Соответственно, характеристика блокирования:
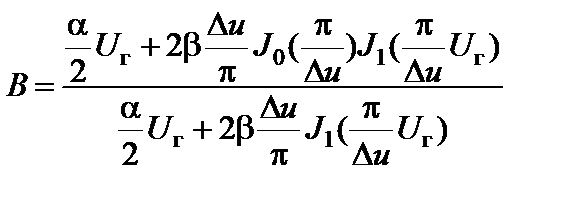. (2.8.22)
Амплитуда интермодуляционного колебания третьего порядка при равноуровневом бигармоническом воздействии описывается уравнением:
(2.8.23)
| B |
| 1,0 |
| 0,5 |
| 0 0,25 0,5 U 1/∆ u |
| x 2/2 |
| 1-cos(x) |
Рис. 2.8.3. Характеристика блокирования преобразователя частоты
| 10-3 |
| 0,001 0,002 0,005 0,01 0,02 0,05 0,1 0,2 0,5 U 1/∆ u |
| U 2f2-f1 ∆ u |
| 10-4 |
| 10-5 |
| 10-6 |
| 10-7 |
Рис. 2.8.4. Зависимость уровня интермодуляционной спектральной
составляющей третьего порядка на выходе преобразователя частоты от уровней компонентов бигармонического входного воздействия
Это выражение не содержит параметр a и полностью совпадает с выражением (2.8.16). Отсюда следует вывод о том, что при том же динамическом диапазоне, который обеспечивается моделью (2.8.4) при заданном параметре Du, модель (2.8.17) позволяет наложить дополнительные условия либо на амплитудную характеристику, либо на характеристику блокирования.
|
|
|
2.9. Синтез передаточной характеристики преобразователя частоты по его
параметрам
В случае, когда продуктами нелинейного взаимодействия колебаний в преобразователе частоты можно пренебречь, целесообразно пользоваться наиболее простой его моделью (2.8.2), для синтеза передаточной характеристики которой достаточно знать коэффициент передачи К. Например, для К = 1 и при U г = 1 для указанной модели имеем a = 0,5.
Однако, при полигармоническом входном воздействии относительно большого уровня требуется учитывать нелинейные явления, которые происходят в преобразователе частоты. В этом случае необходимо, как минимум, пользоваться моделями (2.8.4) или (2.8.17).
Произведем синтез ПХ модели (2.8.4) в предположении, что b1 = b2 = b. Пусть заданы коэффициент передачи преобразователя К и его динамический диапазон D:
, (2.9.1)
который фиксируется для
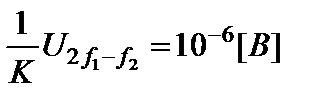. (2.9.2)
Согласно выражению (2.8.13), можно записать следующее равенство:
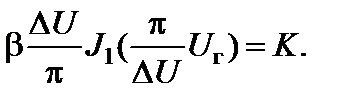(2.9.3)
Из (2.8.16) следует, что при U1 << Du справедливо равенство
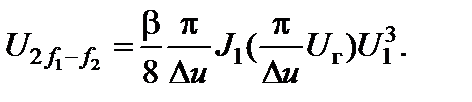(2.9.4)
Решая совместно уравнения (2.9.3) и (2.9.4), находим:
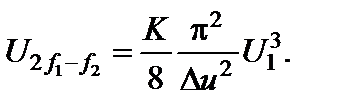(2.9.5)
С учетом (2.9.2), имеем уравнение
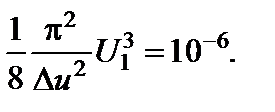(2.9.6)
Так как, согласно (2.9.1)
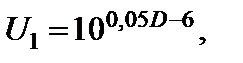(2.9.7)
то из (2.9.6) определим Du:
(2.9.8)
Считая, что U г берется таким, чтобы функция J1((p/D u) U г) достигала экстремума, равного 0,58, находим
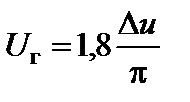(2.9.9)
и, согласно (2.8.13),
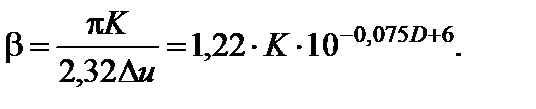(2.9.10)
В таблице 2.9.1 даны значения параметров модели (2.8.4) b/K и D u в зависимости от динамического диапазона D. Здесь же приведены значения уровней гетеродина, обеспечивающие максимальные значения функции J1((p/D u) U г) при заданных D u.
Таблица 2.9.1
Зависимость параметров b, D u и U г от динамического диапазона преобразователя частоты D.
D 60 70 80 90 100
b/K 77,1 13,7 2,44 0,43 0,077
DU [В] 0,035 0,197 1,1107 6,25 35,12
U г [В] 0,02 0,1132 0,6364 3,58 20,1
Далее рассмотрим типовую модель преобразователя частоты вида (2.8.17) при g1 = g2 = 0; a1 = a2 = a; b1 = b2 = b.
Согласно (2.8.20)
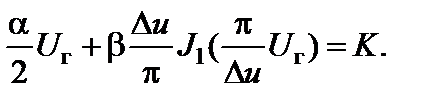(2.9.11)
Для U 1 << D U из (2.8.23) следует равенство, которое обусловлено значением динамического диапазона преобразователя частоты:
(2.9.12)
С учетом (2.8.22) и (2.9.12), имеем равенство
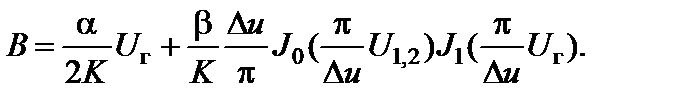(2.9.13)
Из уравнений (2.9.12) и (2.9.13) можно получить выражение
(2.9.14)
Разложив функцию Бесселя J0(x) в степенной ряд и ограничившись первыми тремя членами этого ряда с учетом (2.9.12), из (2.9.14) можно получить следующее уравнение:
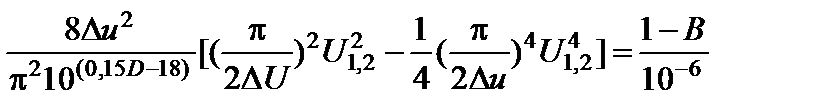. (2.9.15)
Решая это уравнение относительно параметра Du, получаем его значение
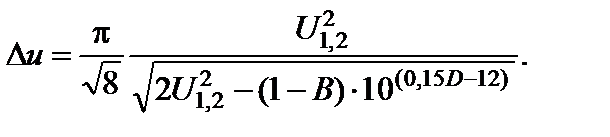(2.9.16)
Зная Du, из (2.9.12) находим параметр b:
(2.9.17)
а из (2.9.13) - параметр a:
|
|
|
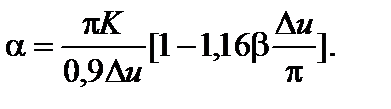(2.9.18)
Таким образом, при заданных характеристиках преобразователя частоты K, B(U 1,2) и D с помощью выражений (2.9.16) - (2.9.18) можно определить параметры его математической модели Du, b и a.
2.10. Аналитические модели ограниченно-идеальных преобразователей частоты
Рассмотрим преобразователь частоты, у которого полуветви передаточной характеристики являются квадратичными параболами на ограниченном интервале изменения уровней воздействующих на его входы колебаний:
(2.10.1)
при условии, что выполняется неравенство
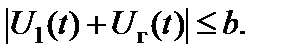(2.10.2)
За пределами заданного интервала [- b, b ] передаточные характеристики полуветвей могут быть продолжены произвольно, в частности, например, так, как показано на рис. 2.10.1, или так, как изображено на рис. 2.10.2. И в том, и в другом случае ПХ являются периодическими функциями и могут быть на интервале [- b, b ] представлены рядами Фурье.
Рассмотрим первую модель, которая соответствует рис. 2.10.1. Можно показать, что при полигармонических входных воздействиях (2.8.8) и (2.8.9), колебание на выходе такого преобразователя описывается следующим выражением:
(2.10.3)
С другой стороны, для ПХ (2.10.1) справедливо равенство
(2.10.4)
Приравнивая подобные члены уравнений (2.10.3) и (2.10.4) при выполнении условий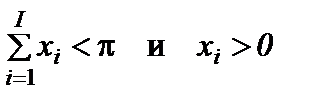 
, получим следующие выражения:
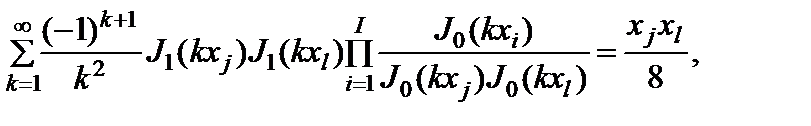(2.10.5)
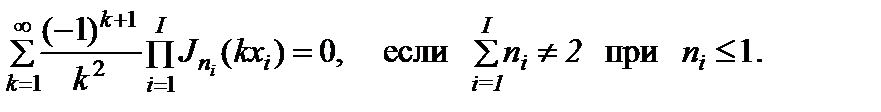(2.10.6)
Из уравнений (2.10.5) и (2.10.6) можно получить частные случаи:
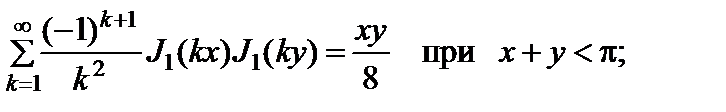(2.10.7)
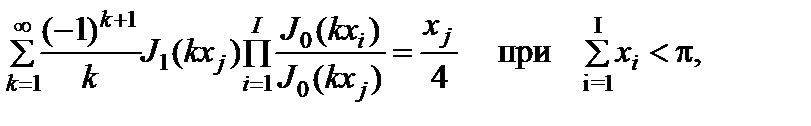(2.10.8)
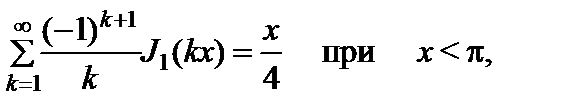(2.10.9)
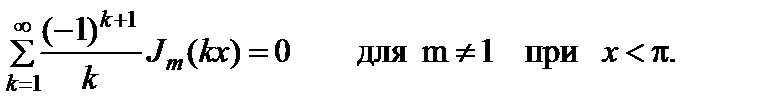(2.10.10)
Последние два равенства являются частными случаями (6.4.3) [139].
Из (2.10.8) следует, что
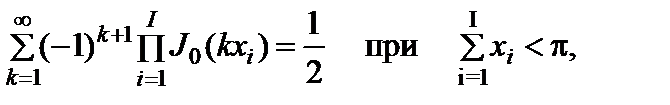(2.10.11)
(2.10.12)
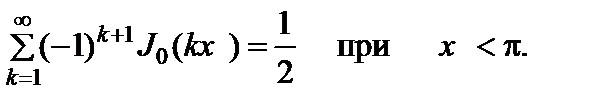(2.10.13)
Последнее равенство совпадает с (8.521) [39].
Из уравнения (2.10.6) следует выражение
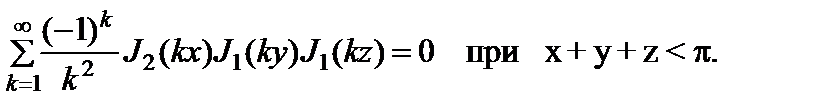(2.10.14)
Известно [18], что
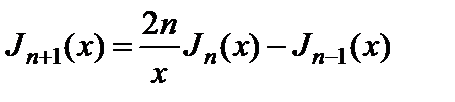. (2.10.15)
С учетом этого, из (2.10.14) можно получить равенство:
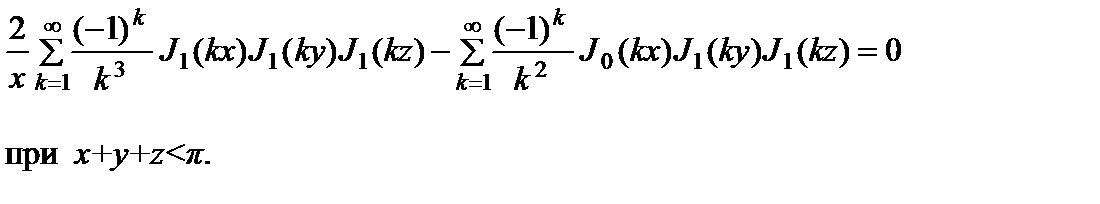(2.10.16)
Согласно (2.10.5) можно записать
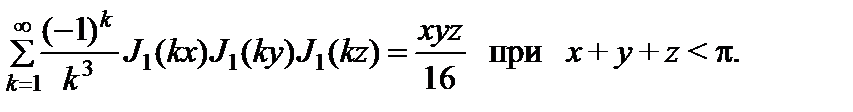(2.10.17)
|
| U2/α |
| 1,0 |
| -3 -2 -1 0 1 2 3 U1/b |
Рис. 2.10.1. Модель № 1 полуветви ограниченно-идеального
преобразователя частоты
|
| -3 -2 -1 0 1 2 3 U1/b |
| U2/α |
| 1,0 |
Рис. 2.10.2. Модель № 2 полуветви ограниченно-идеального преобразователя частоты
Аналогичным образом можно показать справедливость более общего выражения:
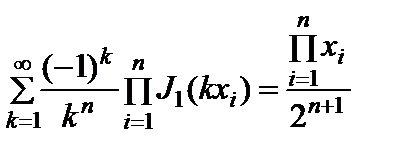. (2.10.18)
Уравнение (2.10.18) справедливо при условии S x i < p и х > 0.
Вышеприведенные равенства могут иметь самостоятельное значение в различного рода физико-математических приложениях.
Пользуясь выражением (2.10.3), можно получить выражения для основных характеристик преобразователя частоты.
Амплитудная характеристика.
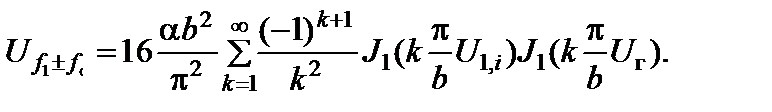(2.10.19)
Характеристика блокирования.
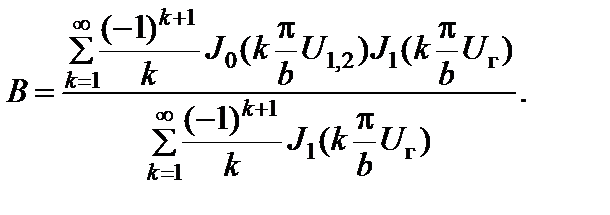(2.10.20)
С учетом (2.10.8) и (2.10.9) при U 1,1+ U 1,2+ U г < b B = 1, т. е. блокирование малого сигнала не происходит.
Амплитуда интермодуляционной составляющей третьего порядкапри равноуровневом бигармоническом входном воздействии
(2.10.21)
Согласно (2.10.6) для 2 U 1 + U г < b U 2f1-f2 = 0.
Далее рассмотрим вторую модель преобразователя частоты. Как и в предыдущем случае, при полигармонических входных воздействиях можно записать выражение для колебания на его выходе в следующем виде:
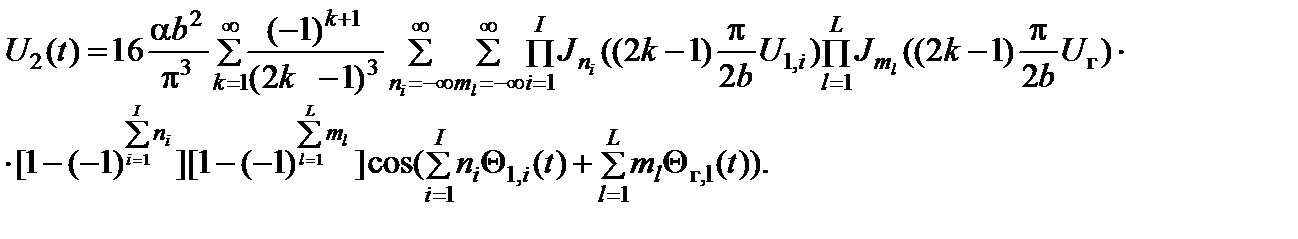(2.10.22)
Сравнивая уравнения (2.10.4) и (2.10.22) для условий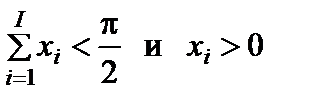 
, можно записать выражения
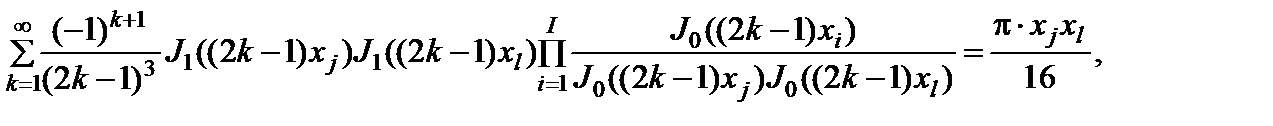(2.10.23)
(2.10.24)
Из (2.10.23) следуют частные случаи:
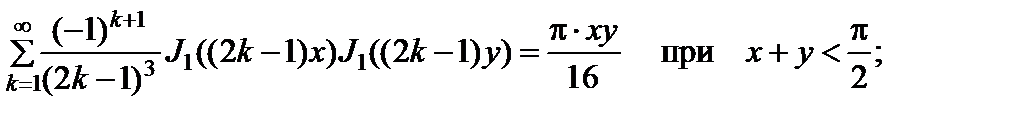(2.10.25)
(2.10.26)
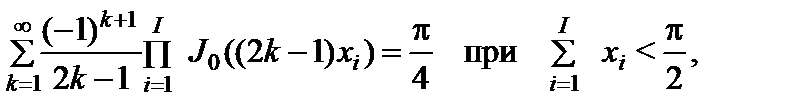(2.10.27)
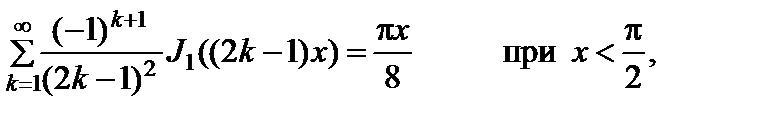(2.10.28)
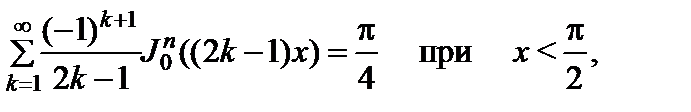(2.10.29)
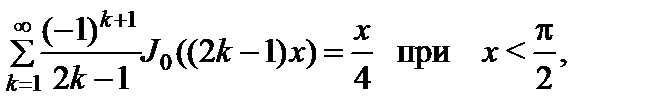(2.10.30)
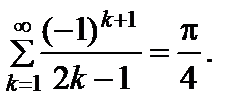(2.10.31)
Последнее равенство полностью совпадает с формулой (0.232) в [39].
Используя выражение (2.10.24), можно показать справедливость следующей формулы:
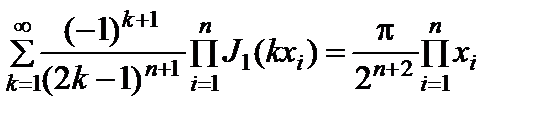. (2.10.32)
Необходимо помнить, что приведенные выше выражения справедливы лишь при выполнении условий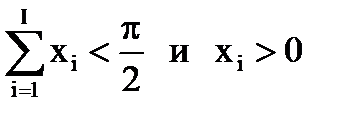 
. Как и в предыдущем случае, полученные равенства могут иметь самостоятельное значение в различного рода физико-математических приложениях.
Пользуясь выражением (2.10.22), можно получить основные характеристики преобразователя, который соответствует второму типу модели.
Амплитудная характеристика.
(2.10.33)
Характеристика блокирования.
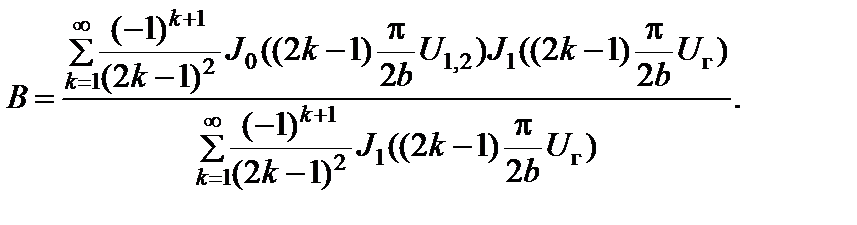(2.10.34)
Амплитуда интермодуляции третьего порядка при равноуровневом бигармоническом входном воздействии.
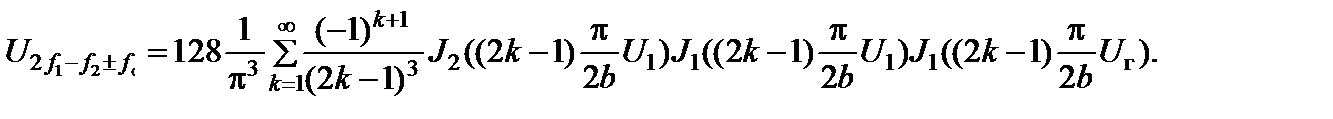(2.10.35)
Исследуем, как зависит точность производимых расчетов с помощью первой и второй моделей в зависимости от числа учитываемых членов ряда Фурье. На рисунке 2.10.3 приведены соответствующие значения относительной погрешности расчетов амплитудных характеристик.
Из рисунка видно, что результаты расчетов, проводимых с помощью второй модели, сходятся к своему пределу намного быстрее, чем результаты, полученные с помощью первой модели. Объясняется это тем, что ПХ первой модели имеет разрыв своей первой производной и, в связи с этим, для достижения заданной точности аппроксимации необходимо увеличивать число учитываемых членов ряда Фурье.
| 10-1 |
| d |
| 10-2 |
| 1,0 |
| 10-3 |
| 10-4 |
| 10-5 |
| 0 5 10 15 20 К |
| 10-6 |
| Модель № 2 |
| Модель № 1 |
Рис. 2.10.3. Зависимость относительной точности оценки значений амплитудной характеристики 1-ой и 2-ой моделей ограниченно - идеального преобразователя от числа учитываемых членов ряда Фурье
| U 2,1 αb2 |
| 1,0 |
| 0,75 |
| 0,5 |
| 0,25 |
| 0 0,5 1,0 1,5 2,0 U 1/b |
|
|
|
