 |
Неравенство Крафта. Прямая теорема неравномерного кодирования. Теорема 12.3.Для ансамбля X ={x, P(x)) с энтропией H(x) существует побуквенный неравномерный префиксный код со средней длиной кодовых слов.
|
|
|
|
Неравенство Крафта
Вернемся к примеру 12. 1 и сравним коды C1 и C2 объема 4. Код C1 равномерный, все слова имеют одинаковую длину 2. Нельзя ли выбрать слова короче? Действительно, в коде C2 есть одно слово длины 1, но чтобы сохранить объем кода и префиксность, пришлось на единицу увеличить длины двух других кодовых слов. Этот пример показывает, что требование префиксности накладывает жесткие ограничения на множество длин кодовых слов и не дает возможности выбирать кодовые слова слишком короткими. Формально эти ограничения записываются в виде изящного неравенства, называемого неравенством Крафта.
Теорема 12. 1. Необходимым и достаточным условием существования префиксного кода объема N с длинами кодовых слов m1, …, mN является выполнение неравенства
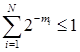(12. 1)
Для достижения равенства в (12. 1) кодовое дерево должно быть полным, т. е. каждая промежуточная вершина дерева должна иметь ровно 2 потомка и всем концевым вершинам должны быть сопоставлены кодовые слова.
Неравенство Крафта как бы ограничивает снизу длины кодовых слов префиксного кода заданного объема N. В связи с этим важно быть уверенным, что оно имеет место и для любых других однозначно декодируемых кодов. Это утверждение является содержанием следующей теоремы.
Теорема 12. 2. Для любого однозначно декодируемого двоичного кода объема N с длинами кодовых слов m1, …, mN справедливо неравенство
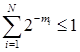. (12. 2)
Прямая теорема неравномерного кодирования
Начнем непосредственно с формулировки теоремы кодирования.
Теорема 12. 3. Для ансамбля X ={x, P(x)) с энтропией H(x) существует побуквенный неравномерный префиксный код со средней длиной кодовых слов.
|
|
|
Обсудим полученную оценку длины кодовых слов. Мы знаем, что достижимая скорость кодирования примерно равна энтропии. Теорема гарантирует, что средняя длина слов хорошего кода отличается от энтропии не больше, чем на 1. Если энтропия велика, то проигрыш по сравнению с минимально достижимой скоростью можно считать небольшим. Но предположим, что H(x)=0, 1. Теорема гарантирует, что существует код со средней длиной кодовых слов не больше 1, 1 бита. Но нам хотелось бы затрачивать на передачу одного сообщение примерно в 10 раз меньше бит! Этот пример показывает, что либо теорема дает неточную оценку, либо побуквенное кодирование в этом случае не эффективно.
На этом же примере мы убедимся в том, что теорема достаточно точна и ее результат не может быть улучшен, если не использовать никакой дополнительной информации об источнике. Действительно, предположим, что дан двоичный источник X={0, 1} с вероятностями букв {e, 1-e}. Минимально достижимая длина кодовых слов наилучшего кода, очевидно, равна 1. Теорема говорит, что средняя длина кодовых слов не больше 1+H(e), т. е. стремится к 1 при e®0. Таким образом, для данного примера двоичного источника теорема точна.
Достижение скоростей (затрат на передачу одной буквы источника) меньших 1 невозможно при побуквенном кодировании, поскольку длина кодового слова не может быть меньше 1. Однако, переход к кодированию блоков сообщений, как мы увидим позже, решает эту проблему и позволяет сколь угодно близко подойти к теоретическому пределу равному энтропии H(x). Конструктивным решением данной задачи является арифметическое кодирование, рассматриваемое в конце данного раздела.
Обратная теорема неравномерного кодирования
Обратная теорема неравномерного кодирования устанавливает нижнюю границу средней длины кодовых слов любого однозначно декодируемого кода.
|
|
|
Теорема 12. 4. Для любого однозначно декодируемого кода дискретного источника X ={x, P(x)) с энтропией H(x) средняя длина кодовых слов 
удовлетворяет неравенству
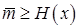. (12. 3)
Другими словами, не существует кода со средней длиной кодовых слов меньше H(x) и обладающего свойством однозначной декодируемости.
Рассмотрим вопрос о том, при каких условиях возможно равенство в обратной теореме. Перепишем неравенство (12. 3):
Для этого при каждом x должно выполняться соотношение 
. В то же время для такого распределения вероятностей существует полный префиксный код с длинами кодовых слов mi = é -log P(xi)ù = -log P(xi). Для этого кода неравенство Крафта выполняется с равенством средняя длина кодового слова 
.
Таким образом, мы установили справедливость следующего утверждения.
Следствие. Необходимым условием существования кода со средней длиной кодовых слов необходимо, чтобы все вероятности сообщений xi Î X имели вид , где {mi} – целые положительные числа.
|
|
|
