 |
Оптимальный код – код Хаффмана
|
|
|
|
Оптимальный код – код Хаффмана
Предложенный Хаффманом алгоритм построения оптимальных неравномерных кодов – одно из самых важных достижений теории информации как с теоретической, так и с прикладной точек зрения. Трудно поверить, но этот алгоритм был придуман в 1952 г. студентом Дэвидом Хаффманом в процессе выполнения домашнего задания.
Рассмотрим ансамбль сообщений X = {1, …, N} с вероятностями сообщений {P1, …, PN}. Без потери общности мы считаем сообщения упорядоченными по убыванию вероятностей, т. е. P1≤ P2≤ …≤ PN. Наша задача состоит в построении оптимального кода, т. е. кода с наименьшей возможной средней длиной кодовых слов. Понятно, что при заданных вероятностях такой код может не быть единственным, возможно существование семейства оптимальных кодов. Мы установим некоторые свойства всех кодов этого семейства. Эти свойства подскажут нам простой путь к нахождению одного из оптимальных кодов.
Пусть двоичный код 
с длинами кодовых слов {m1, …, mN} оптимален для рассматриваемого ансамбля сообщений.
Свойство 1. Если Pi < Pj, то mi > mj.
Свойство 2. Не менее двух кодовых слов имеют одинаковую длину mmax= maxk mk.
Свойство 3. Среди кодовых слов длины mmax = maxk mk найдутся 2 слова, отличающиеся только в одном последнем символе.
Прежде, чем сформулировать следующее свойство, введем дополнительные обозначения. Для рассматриваемого ансамбля X={1, …, N} и некоторого кода C, удовлетворяющего свойствам 1–3, введем вспомогательный ансамбль X’={1, …, N-1}, сообщениям которого сопоставим вероятности {P’1, …, P’N} следующим образом
.
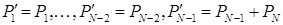Из кода C построим код C' для ансамбля X', приписав сообщениям 
те же кодовые слова, что и в коде C, т. е. 
, i = 1, …, N-2, а сообщению 
– слово 
, представляющее собой общую часть слов и 
(согласно свойству 3 эти два кодовых слова отличаются только в одном последнем символе).
|
|
|
Свойство 4. Если код C' для X' оптимален, то код C оптимален для X.
Итак, сформулированные свойства оптимальных префиксных кодов сводят задачу построения кода объема N к задаче построения кодов объема N' = N - 1. Это означает, что мы получили рекуррентное правило построения кодового дерева оптимального неравномерного кода.
Алгоритм построения кодового дерева кода Хаффмана.
1. Инициализация. Список «подлежащих обработке» узлов состоит из N0 = N узлов, каждому из которых приписана вероятность одного из сообщений.
2. До тех пор, пока число узлов N0 > 1, повторяются следующие действия:
В списке необработанных узлов находим два узла с наименьшими вероятностями. Они исключаются из списка и вместо них вводится новый узел, которому приписывается суммарная вероятность двух исключенных узлов. Новый узел связывается ребрами с исключенными узлами. Число необработанных узлов N0 уменьшается на 1, N0 N0 - 1
После выполнения алгоритма будет получено кодовое дерево кода, который, как доказано выше, имеет наименьшую возможную среднюю длину кодовых слов.
Пример. 12. 3. Рассмотрим ансамбль буквенных сообщений {a, b, c, d, e, f} вероятностями букв {0, 35, 0, 2, 0, 15, 0, 1, 0, 1, 0, 1} соответственно. Кодовое дерево и код Хаффмана показаны на рис. 12. 2. Энтропия источника H(x) = 2, 4016. Средняя длина кодовых слов равна 
=2, 45. Согласно свойствам 1-4 не существует кода для X со средней длиной кодовых слов меньшей, чем 2, 45.
Избыточность кода Хаффмана
Из теоремы 12. 3 следует, что для построенных по алгоритму Хаффмана кодов средняя длина кодовых слов удовлетворяет неравенству
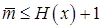, (12. 4)
|
|
|
где H(x) – энтропия ансамбля.
Разность 
называется избыточностью неравномерного кода. При кодировании с избыточностью r на каждое сообщение тратится на r бит больше, чем в принципе можно было бы потратить, если использовать теоретически наилучший (возможно, нереализуемый) способ кодирования.
Итак, из (12. 4) следует, что для кода Хаффмана избыточность r ≤ 1. Хотелось бы получить более точную оценку средней длины кодовых слов. Р. Галлагер, получил гораздо более точную оценку избыточности, наложив ограничение на максимальную из вероятностей сообщений.
Теорема 12. 5. Пусть P1 – наибольшая из вероятностей сообщений конечного дискретного ансамбля. Тогда избыточность кода Хаффмана для этого ансамбля удовлетворяет неравенствам
где H(P1) = –P1 log P1 – (1– P1)log(1– P1) – энтропия двоичного ансамбля, и
s = 1 – log e – log log e » 0, 08607.
|
|
|
