Код Шеннона - Фано. Неравномерное кодирование для последовательности сообщений

Код Шеннона - Фано

Рассмотрим источник, выбирающий буквы из множества X ={1,..., N} с вероятностями {P₁, …, P_N}. Считаем, что буквы упорядочены по убыванию вероятностей, т. е. P₁ ≥ P₂ ≥ … ≥ P_N.

Кодирование Шеннона-Фано имеет большое сходство с кодированием Хаффмана. Рассмотрим алгоритм вычисления кодов Шеннона-Фано (для наглядности возьмём в качестве примера последовательность 'aa bbb cccc ddddd'. Для вычисления кодов, необходимо создать таблицу уникальных символов сообщения x_i и их вероятностей P(x_i), и отсортировать её в порядке невозрастания вероятности символов.

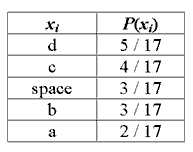
Далее, таблица символов делится на две группы таким образом, чтобы каждая из групп имела приблизительно одинаковую частоту по сумме символов. Первой группе устанавливается начало кода в '0', второй в '1'. Для вычисления следующих бит кодов символов, данная процедура повторяется рекурсивно для каждой группы, в которой больше одного символа. Таким образом для нашего случая получаем следующие коды символов:

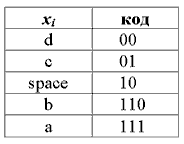
Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса (разве что как упражнение в учебных целях). В большинстве случаев, длина закодированной последовательности, по данному методу, равна длине закодированной последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях всё же формируются не оптимальные коды Шеннона-Фано, поэтому сжатие методом Хаффмана принято считать более эффективным. Такие отличии в степени сжатия возникают из-за нестрогого определения способа деления символов на группы.

Неравномерное кодирование для последовательности сообщений

В этом параграфе мы перейдем к решению задачи кодирования последовательностей сообщений. Разумеется, если мы рассматриваем стационарный источник и его распределение вероятностей на буквах не меняется от буквы к букве, то любой из описанных выше способов кодирования может быть использован для кодирования отдельных сообщений источника. Во многих случаях именно такой подход используется на практике как самый простой и достаточно эффективный.

В то же время, можно выделить класс ситуаций, когда побуквенное кодирование заведомо неоптимально. Во-первых, из теоремы об энтропии на сообщение стационарного источника следует, что учет памяти источника потенциально может значительно повысить эффективность кодирования. Во-вторых, побуквенные методы затрачивают как минимум 1 бит на сообщение, тогда как энтропия на сообщения может быть значительно меньше 1.

Итак, рассмотрим последовательность x₁, x₂, …, x_i Î X = {x_i}, наблюдаемую на выходе дискретного стационарного источника, для которого известно вероятностное описание, т. е. можно вычислить все многомерные распределения вероятностей и по ним – энтропию H(x) = H_¥ (X).

Пусть указан некоторый способ кодирования, который для любых n для каждой последовательности 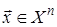 на выходе источника строит кодовое слово  длины 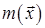. Тогда средняя длина кода на сообщение, для блоков длины n определяется как

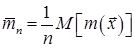 бит/сообщение источника.

Подбирая длину блоков, при которой средняя длина кода будет наименьшей, получаем следующее определение для средней длины кода на сообщение

.

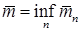(Мы пишем нижнюю грань inf вместо минимума, поскольку наименьшее значение скорости может достигаться в пределе при n ® ¥ ).

Рассматриваемое кодирование называется FV-кодированием (fixed-to-variable), поскольку блоки из фиксированного числа сообщений n кодируются кодовыми словами переменной длины. Наша задача – связать достижимые значения средней скорости FV-кодирования с характеристиками источника, в частности, с его энтропией H(x). Начнем с обратной теоремы кодирования.

Теорема 12. 6. Для дискретного стационарного источника с энтропией H(x) для любого FV-кодирования имеет место неравенство

.
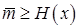