3.2.  Измерение  связи между  политомичными переменными (таблица сопряженности m x p ).

Если переменные, измеренные на номинальной шкале, имеют более двух градаций, то они называются политомичными. Измерение связи между такого рода переменными осуществляется с помощью специальных показателей  – коэффициентов взаимной сопряженности. К коэффициентам взаимной сопряженности относятся коэффициенты К. Пирсона, А. Чупрова, Г. Крамера.

Коэффициенты взаимной сопряженности основаны на критерии хи – квадрат Пирсона. Эти меры связи принимают значения в интервале от 0 до +1. Равенство нулю любого из этих показателей означает отсутствие связи, т. е. полную независимость, а равенство единице  - полную связь между переменными.

Если переменная X имеет m – градаций,  а переменная  Y имеет    p – градаций, то    таблица  сопряженности  переменных X и Y  размером m x p будет  иметь следующий  вид:

Таблица 3. 3. Таблица сопряженности между политомичными переменными размером m x p

 

y x			…j…	p	Всего
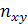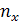
… I … m	… … … … … …	… … … … … …	… … … … 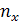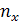… …	… … … … …	… … nx
Итого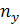

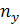
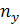
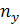
Такая таблица используется для расчета различных   коэффициентов взаимной сопряженности:

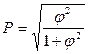      - коэффициент взаимной сопряженности Пирсона     (3. 6)

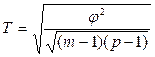    - коэффициент взаимной сопряженности Чупрова (3. 7)

- коэффициент взаимной сопряженности Крамера (3. 8)

В представленных выше  формулах 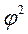- показатель взаимной сопряженности, который вычисляется следующим образом:

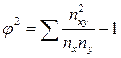           или                             (3. 9)

Считается, что коэффициент взаимной сопряженности Чупрова более строго оценивает тесноту связи, чем показатель Пирсона, так как коэффициент

Пирсона не достигает максимального значения +1 даже при полной связи переменных, он лишь стремиться к этому значению при увеличении числа градаций переменных.  Коэффициент взаимной сопряженности Чупрова характеризует долю фактической сопряженности переменных в их полной сопряженности, а квадрат этого показателя имеет смысл коэффициента детерминации.

       Коэффициент взаимной сопряженности Крамера рассчитывается только  для  неквадратных таблиц  сопряженности  и учитывает минимальную из величин: или число строк, или число столбцов таблицы  сопряженности.

Пример 3. 2.  Имеются данные о распределении студентов четырех факультетов экономического вуза,  оценивавших  степень сложности математических дисциплин, изучаемых в вузе:

Таблица 3. 4.   Таблица сопряженности между переменными « место учебы респондента (факультет)» и «оценка степени сложности математических дисциплин, изучаемых в вузе».

 

Факультет	Оценка степени сложности математических дисциплин				Всего
	Очень сложные	Не очень сложные	Совсем не сложные	Затрудняюсь ответить
Экономический Финансовый Менеджмента Коммерции
Итого

 

Определить коэффициенты взаимной сопряженности Пирсона и Чупрова.

Решение:

;

 

 

 

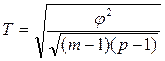
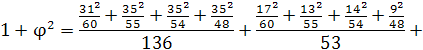
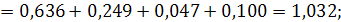
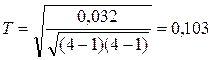
Вывод: Связь между оценкой студентами степени сложности  математических дисциплин  и местом их обучения (факультетом) слабая, т. е. такая оценка практически  не зависит от факультета, на котором учатся студенты.

Cуществуют  модификации коэффициентов  Пирсона и Чупрова, основанные на 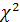-критерии Пирсона. Модифицированный коэффициент взаимной сопряженности  Пирсона вычисляется по формуле:

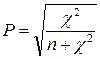      (3. 10),         где  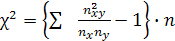      (3. 11)

Модифицированный коэффициент сопряженности Чупрова  вычисляется следующим образом:

 ,                                                           (3. 12)  

где k₁ – число строк в таблице;

 k₂ – число граф в таблице;

 n – число наблюдений.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: