 |
4.2. Другие меры связей между переменными, измеренными на номинальной шкале.
|
|
|
|
Построение теоретико-информационных мер может осуществляться не только на основе энтропии. Примером может служить коэффициент Валлиса. Коэффициент Валлиса интересен тем, что он прямо отвечает принципу построения мер связи как характеристик относительного уменьшения вероятности ошибки предсказания переменной Y, зная переменную X, в
сравнении с вероятностью ошибки предсказания Y, не зная X. Этот показатель вычисляется по формуле:
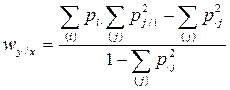, (4. 7)
где 
- это 
я частость в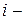 
той строке таблицы совместного распределения переменных X и Y.
Свойства коэффициента Валлиса подобны свойствам 
:
1) 
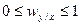
2) 
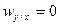, если переменные статистически независимы;
3) 
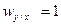, если X полностью детерминирует Y;
4) 
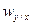инвариантен по отношению к перестановке местами строк или столбцов таблицы.
Коэффициент Валлиса показывает пропорциональную редукцию ошибок предсказания. Другими словами, если, например, 
, то мы можем дать этой величине очень простую интерпретацию: знание X уменьшает число ошибок прогноза вдвое. Тем самым оценивается возможность правильного предсказания принадлежности объекта к категории по Y, если известна его принадлежность к 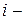категории по X и одновременно оценивается величина тесноты связи между признаками X и Y.
Рассмотрим семейства мер связи l-Гутмана и t-Гудмена и Краскала. Это меры связи, включающие асимметричные меры и симметричную меру связи: lb, la, l и tb, t, a t.
Теоретико-вероятностную интерпретацию имеют коэффициенты Гутмана. Эти показатели основаны на том, что если рассматриваемые переменные зависимы, то информация о том, какое значение принял первый из них, должна улучшать точность предсказания значения второго признака.
|
|
|
Коэффициент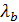 
- Гутмана вычисляется по формуле:
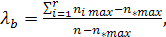(4. 8)
Где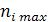 
- максимальная частота i-строки;
– максимальный элемент итоговой строки.
Коэффициент 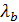ассиметричный показатель, т. к. изучает зависимость Y от X. Статистика 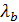основана на сравнении двух ситуаций. Для случайно взятого наблюдения мы угадываем его Y-категорию, во-первых, если нет никакой дополнительной информации о его категории в X, и, во-вторых, если известен его класс в категории X.
В первом случае для того, чтобы максимизировать вероятность угадать категорию признака Y, мы должны выбрать градацию с максимальной маргинальной частотой n*j, т. е. выбрать maxj n*j.
Если известна категория признака X, то необходимо выбирать максимальное число в этой строке. Очевидно, что если признаки взаимосвязаны, то знание категории X позволяет достигать лучшего предсказания.
Коэффициент 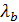оценивает снижения вероятности ошибки предсказания признака Y при известной информации о принадлежности наблюдения к классу признака X по сравнению с ситуацией, когда такой информации нет.
Коэффициент 
- Гутмана эквивалентен коэффициенту 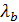, с учетом перемены строк и столбцов между собой. Он является ассиметричным коэффициентом и определяет степень зависимости X от Y.
(4. 9)
Где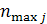 
- max частота j-го столбца.
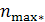- max элемент итогового столбца.
Коэффициент измеряет улучшение средней величины относительного изменения вероятности ошибки предсказания категории признака, располагающегося по столбцам таблицы, при изменении категорий признака располагающегося по строкам.
Если при анализе таблиц сопряженности не имеет значения последовательность расположения классов по признакам, т. е. неважно, зависит X от Y или наоборот, то используется коэффициент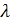 
. Этот коэффициент находит усредненную величину прогноза между изучаемыми переменными.
|
|
|
(4. 10)
где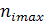 
= 
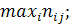
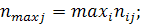
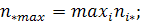
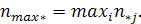
Коэффициент 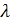определяется как результат объединения 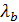и :
min (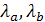 
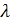) ≤ ≤ max ( 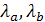). (4. 11)
При построении коэффициентов Гутмана возникают трудности, связанные с неравномерным расположением условных сумм (обращение коэффициентов 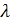в ноль). Меры l-Гутмана имеют тот недостаток, что они принимают нулевое значение, если все максимальные клеточные частоты оказываются в одном и том же столбце или в одной и той же строке таблицы. В этом случае числители коэффициентов 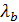и равны 0, однако это может не означать независимости исследуемых переменных.
Этот недостаток устраняется в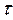 
- коэффициентах Гудмена и Краскала. Различие заключается в ином методе предсказания категории одной переменной при известной категории для другой. Вместо того чтобы всегда предсказывать наиболее вероятную категорию, 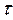-меры предсказывают различные категории в пропорции, которая имеет место для наблюдаемых итогов.
Коэффициент 
сравнивает случайный, пропорциональный прогноз признака Y со вторым признаком X и рассчитывает условное, пропорциональное предсказание класса Y, при предложении, что имеется информация о принадлежности объекта к одному из классов признака X. Этот коэффициент связи является ассиметричным коэффициентом.
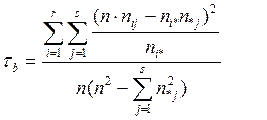(4. 12)
При прогнозировании категорий признака X в зависимости от Y, то есть строк таблицы сопряженности в зависимости от столбцов, применяется коэффициент 
:
(4. 13)
Данная мера, умноженная на 100%, показывает, на сколько процентов уменьшится неправильный прогноз категории признака X для случайно взятого объекта при условном пропорциональном прогнозировании по сравнению с безусловным пропорциональным прогнозом.
Для получения симметричной меры 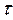случайно выбранный объект с вероятностью ½ прогнозируется по признаку X или по признаку Y. Этот симметричный коэффициент получается в виде усредненных коэффициентов и :
|
|
|
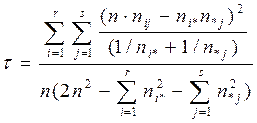(4. 14)
Коэффициенты ,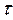 
, 
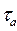удовлетворяют неравенству:
(4. 15)
Меры связи t ближе по своей конструкции к статистике χ 2 и являются более надежными мерами, нежели l.
Пример 4. 2. В результате проведенного опроса выпускников вузов относительно их планов о дальнейшем продолжении обучения в вузе и фактической их реализации получена следующая комбинационная таблица:
Таблица 4. 2. Таблица сопряженности между переменными « планы выпускников вузов о дальнейшем образовании» и «фактическая реализация планов»
| Планы опрошенных | Фактическое распределение | |||
| Пошли работать | Поступили в магистратуру | Поступили в вуз для получения второго высшего образования | Итого | |
| Пойти работать | ||||
| Поступить в магистратуру | ||||
| Получить второе высшее образование | ||||
| Итого | ||||
Решение: Рассчитаем точечные оценки коэффициентов 
.
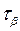
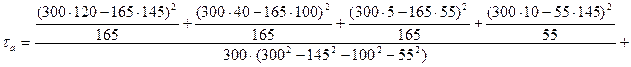
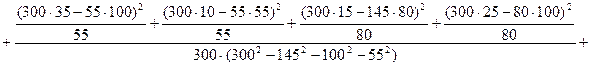
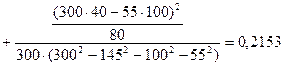
Аналогично находим коэффициент 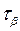= 0, 2426, , т. е. знание того, известны ли нам планы респондентов на 24% повышает вероятность предсказания фактической реализации планов выпускников. Значение симметричной меры составило 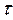= 23, 44%
Для расчетов точечных оценок мер 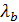и удобно воспользоваться следующей таблицей:
Таблица 4. 3. Вспомогательная таблица для расчета показателе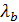й и
| X/Y |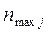 
| |||
|
| 
|
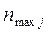
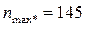
В последнем столбце содержатся максимальные элементы по каждой строке комбинационной таблицы, в последней строке – максимальные элементы по каждому из столбцов.
Определим значения 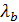и :
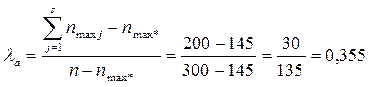
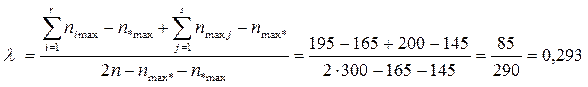
Вывод: Зафиксировав планы выпускников вузов о продолжении образования, возможно на 22% точнее предсказать форму их послевузовского образования. Отклонение реализации планов составляет 35%, а симметричная мера связи составила 29%, т. е. знание обеих переменных на 29% повышает вероятность предсказания принадлежности респондентов к той или иной категории.
|
|
|
|
|
|
