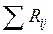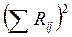|
3.3. Измерение тесноты связи между дихотомическими переменными и переменными, измеренными на интервальной шкале.
|
|
|
|
3. 3. Измерение тесноты связи между дихотомическими переменными и переменными, измеренными на интервальной шкале.
Для оценки тесноты связи между дихотомическими переменными и количественными переменными, измеренными на интервальной шкале, используется биссериальный коэффициент корреляции:
 (3. 13)
(3. 13)
где  – средние в группах;
– средние в группах;
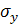 – среднее квадратическое отклонение фактических значений признака от среднего уровня;
– среднее квадратическое отклонение фактических значений признака от среднего уровня;
n1, n2 - число единиц в соответствующих группах;
n - число единиц во всей совокупности.
Биссериальный коэффициент корреляции принимает значения в интервале от 0 до +1.
Пример 3. 3. На основании данных о распределении пользователей интернета по возрастным группам оценить с помощью биссериального коэффициента корреляции зависимость между частотой использования интернета и возрастом респондентов.
Таблица 3. 5. Таблица сопряженности между переменными « частота использования интернета» и «возраст респондентов».
| Категории респондентов | Возраст респондентов (лет) | Всего | |||
| До 25 | 25-35 | 35-45 | Более 45 | ||
| Часто используют интернет | |||||
| Не часто используют интернет | |||||
| Итого | |||||
Решение: Необходимо найти значение биссериального коэффициента корреляции:
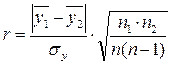
Найдем значения среднего возраста для каждой из двух групп респондентов:

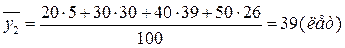
Найдем значение среднего возраста для двух групп (общую среднюю):
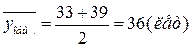
Определим среднее квадратическое отклонение возраста по двум группам:
|
|
|
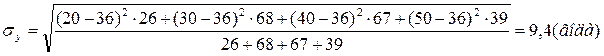
Найдем значение биссериального коэффициента корреляции:
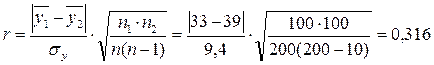
Вывод: Между частотой использования интернета и возрастом респондентов имеет место слабая корреляционная связь.
3. 4. Порядковая шкала. Измерение связи между порядковыми переменными.
Для изучения связи между порядковыми переменными применяются показатели, оценивающие тесноту связи на основе рангов. Это коэффициенты ранговой корреляции Спирмена и Кендалла. Эти коэффициенты могут быть использованы для определения тесноты связи как между качественными, так и между количественными переменными при условии, если их значения будут упорядочены или проранжированы по степени убывания или возрастания значений.
Коэффициент корреляции рангов Спирмена рассчитывается по формуле (при отсутствии связных рангов):
 (3. 14)
(3. 14)
где 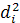 - квадраты разности рангов;
- квадраты разности рангов;
n – число наблюдений (число пар рангов).
Этот показатель принимает любые значения в интервале от –1 до + 1. Значимость коэффициента корреляции рангов Спирмена проверяется на основе t-критерия Стьюдента. Расчетное значение критерия определяется по формуле:
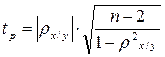 (3. 15)
(3. 15)
Значение коэффициента корреляции рангов Спирмена считается статистически значимым, если tp > tkp (α; k = n - 2).
Если при ранжировании данных появляются связные ранги, то расчет коэффициента корреляции рангов Спирмена производят по формуле:
 , (3. 16)
, (3. 16)
где Тx и Тy – число связных рангов, которое вычисляется по формуле:
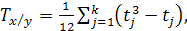 (3. 17)
(3. 17)
где 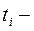 число связных рангов по отдельным переменным.
число связных рангов по отдельным переменным.
Коэффициент корреляции рангов Кендалла рассчитывается по формуле:
|
|
|
 , (3. 18)
, (3. 18)
где n – число наблюдений;
S – сумма разностей между числом последовательностей и числом инверсий по второму признаку (Y).
Коэффициент корреляции рангов Кендалла принимает любые значения в интервале от –1 до + 1.
Существует определенная последовательность расчета этого показателя:
1. Значения переменной X ранжируется строго в порядке возрастания или убывания;
2. Значения переменной Y располагаются в порядке, соответствующем значениям переменной X.
3. Для каждого ранга Y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяют величину Р как меру соответствия последовательностей рангов по X и Y. Она учитывается со знаком «плюс»;
4. Для каждого ранга Y определяется число следующих за ним рангов, меньших его величины. Суммарная величина обозначается через Q и фиксируется со знаком «минус»;
5. Определяется сумма баллов S = (P+Q).
При наличии связанных рангов расчет коэффициента корреляции рангов Кендалла необходимо производить по следующей формуле:

(3. 19)
где vx/y - число связных рангов, которое вычисляется по формуле:
 (3. 20)
(3. 20)
Для проверки статистической значимости коэффициента корреляции рангов Кэндэлла ( при n > 10) вычисляется расчетное значение tрасч. . по формуле:
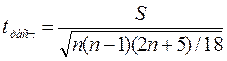 (3. 21)
(3. 21)
Затем для заданного уровня значимости  по таблице нормального распределения определяется
по таблице нормального распределения определяется 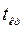 , сравнивается с
, сравнивается с 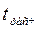 и принимается соответствующее решение.
и принимается соответствующее решение.
Если по одному и тому же набору данных рассчитаны оба коэффициента корреляции рангов, то коэффициент Кендэлла обычно оказывается меньше, чем коэффициент Спирмена:  .
.
Пример 3. 4. Группа экспертов составила рейтинг 10 вузов перед началом вступительных экзаменов в зависимости от степени привлекательности вузов для абитуриентов. Затем вузы оценивались после вступительных экзаменов по результатам зачисления. Оценить насколько точно экспертные оценки совпадают с фактическим результатом.
Таблица 3. 6. Расчетная таблица для вычисления коэффициента корреляции
|
|
|
рангов Спирмена
| Номер вуза | Ранг вуза по оценкам экспертов Rx | Ранг вуза по результатам зачисления Ry | Разность рангов
|
| |
| -2 -1 -4 -1 -1 | |||||
| Итого | - | - | - | 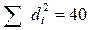
|
Решение: Определим значение коэффициента корреляции рангов Спирмена:
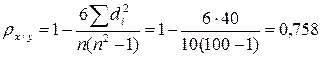
Вывод: Между оценками вузов, данными экспертами перед началом вступительных экзаменов и по результатам зачисления, имеет место достаточно тесная положительная зависимость.
Определим значение коэффициента корреляции рангов Кендэлла. Для этого сначала заполним вспомогательную таблицу, перечисляя Rx строго в порядке возрастания значений, а Ry - в соответствии со значениями показателя X в исходных данных.
Таблица 3. 7. Расчетная таблица для вычисления коэффициента корреляции рангов Кендэлла.
| Ранг вуза по оценкам экспертов Rx (в порядке возрастания значений) | Ранг вуза по результатам зачисления Ry(в порядке соответствующем X) |
Подсчет баллов
| ||
| «+» |
«-» | |||
|
- | - | |||
| Итого | - | Р =+ 35 | Q =-10 | |
Решение: Найдем значение S = P+Q =35 – 10 = 25
Вычислим коэффициент корреляции рангов Кендэлла по формуле:

Вывод: Между оценками вузов, данными экспертами перед началом вступительных экзаменов и по результатам зачисления, имеет место заметная положительная зависимость. Необходимо отметить, что коэффициент корреляции рангов Кендэлла дает более строгую оценку связи, чем коэффициент корреляции рангов Спирмена.
Для характеристики зависимости между несколькими переменными, измеренными на порядковой шкале, рассчитывается коэффициент конкордации (множественный коэффициент ранговой корреляции). Этот показатель вычисляется по формуле:
 , (3. 22)
, (3. 22)
|
|
|
где S - отклонение суммы квадратов рангов от средней квадратов рангов;
m - число порядковых переменных;
n - объем выборки.
Коэффициент конкордации принимает значения в интервале от 0 до +1.
Значимость коэффициента конкордации проверяется на основе 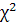 – критерия Пирсона:
– критерия Пирсона:
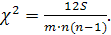 (3. 23)
(3. 23)
Расчетное значение  сравнивается с критическим
сравнивается с критическим 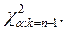 Если расчетное значение
Если расчетное значение  оказывается больше критического
оказывается больше критического 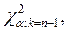 то коэффициент конкордации считается статистически значимым.
то коэффициент конкордации считается статистически значимым.
В случае наличия связных рангов коэффициент конкордации определяется по формуле:
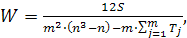 (3. 24)
(3. 24)
где  (3. 25)
(3. 25)
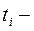 число связных рангов по отдельным переменным.
число связных рангов по отдельным переменным.
Для оценки значимости коэффициента конкордации в этом случае расчетное значение критерия  определяется по формуле:
определяется по формуле:
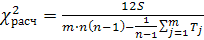 (3. 26)
(3. 26)
Коэффициент конкордации обычно используется для оценки согласованности мнений экспертов о влиянии различных признаков на результативную переменную.
Пример 3. 5. Экспертами проранжированы 4 популярных продукта бытовой химии по трем показателям: качеству, рекламному продвижению на рынке аналогичных товаров и спросу на эти продукты. Сделать выводы о тесноте связи между этими показателями, рассчитав коэффициент конкордации.
Таблица 3. 8. Расчетная таблица для вычисления коэффициента
конкордации
| Порядковый номер продукта | Ранги по показателям | Сумма Рангов
| Квадрат суммы рангов
| ||
| Качество Rx | Рекламное продвижение Ry | Спрос Rz | |||
| Итого | - | - | - | 30 | 262 |
Решение: Найдем значение S:
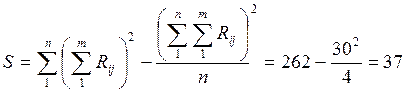
Определим значение коэффициента конкордации:
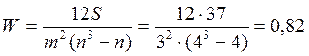
Вывод: Значение коэффициента конкордации 
 позволяет сделать
позволяет сделать
вывод о достаточно сильной зависимости между рассмотренными показателями. Для того, чтобы убедиться в справедливости этого утверждения, необходимо проверить статистическую значимость рассчитанного коэффициента конкордации с помощью 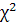 – критерия Пирсона:
– критерия Пирсона:
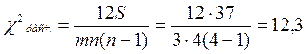
Критическое значение  . Очевидно, что
. Очевидно, что 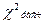 >
> 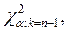 таким образом на уровне значимости
таким образом на уровне значимости 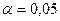 вычисленный коэффициент конкордации можно считать существенным, а зависимость между исследуемыми показателями неслучайной.
вычисленный коэффициент конкордации можно считать существенным, а зависимость между исследуемыми показателями неслучайной.
|
|
|
|
|
|



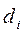 =Rx-Ry
=Rx-Ry