 |
Вопросы для самоконтроля. ТЕМА 4. « Теоретико-информационный подход к построению мер связи для номинального уровня измерения».
|
|
|
|
Вопросы для самоконтроля
1. Какие показатели тесноты связи используются для дихотомических переменных?
2. Что такое ранг?
3. Если переменная X измерена на интервальной шкале, а переменная Y – на номинальной шкале, то какие меры связи можно рассчитать для этих переменных?
4. Какие значения могут принимать коэффициенты ранговой корреляции Спирмена и Кендалла?
5. При измерении связи между номинальными переменными значения переменных участвуют в расчетах мер связи или нет?
6. Почему коэффициенты взаимной сопряженности Пирсона и Чупрова принимают только положительные значения?
7. Как проверяется значимость коэффициента конкордации?
8. Какой особенностью отличается коэффициент взаимной сопряженности Крамера?
9. Какой смысл имеет квадрат коэффициента сопряженности Чупрова?
10. Для чего используется коэффициент конкордации?
ТЕМА 4. « Теоретико-информационный подход к построению мер связи для номинального уровня измерения».
4. 1. Меры связи, основанные на величине количества информации.
Все рассмотренные выше показатели связи для переменных, измеренных на номинальной шкале, обычно сконструированы таким образом, что нулевое значение меры связи должно означать независимость переменных X и Y. Однако выполнение этого условия связано с рядом ограничений, например: наличие большого объема выборки, большое число строк и столбцов в таблице сопряженности и т. д. Все эти ограничения связаны с тем, что показатели взаимной сопряженности основаны на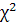 
– критерии Пирсона. Нарушение этих ограничений может приводить к тому, что даже нулевое значение показателя взаимной сопряженности может не означать независимости переменных.
|
|
|
Для измерения статистической связи между двумя переменными очень важным является понятие полной связи. На практике наиболее удобно использовать такие меры связи, верхний предел которых равен единице, и поэтому большинство из них нормировано таким образом, чтобы могло принимать значение, равное 1, в случае, когда между X и Y существует полная связь. Современная трактовка полной связи предполагает, что полная связь между переменными X и Y имеет место в том случае, когда значение X или Y устраняет всякую неопределенность (энтропию) того, какое значение примет Y или X. При этом уменьшение неопределенности всегда связано с получением некоторой информации. Такой подход используется при построении теоретико-информационных мер связи, основанных на величине количества информации I(y, x).
Количество информации – это мера, уменьшающая неопределенность знаний. Количество информации измеряется в битах. 1 бит – это единица информации, содержащаяся в сообщении, уменьшающем неопределенность знаний в 2 раза. Определение количества информации о переменной Y за счет знания переменной X основывается на вычислении полной и условной энтропии переменной Y.
Вычисление полной энтропии распределения переменной Y
связано с оцениванием неопределенности распределения переменной Y (без учета знания переменной X):
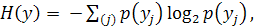(4. 1)
где j – номер категории переменной Y;
р(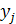 
) – вероятность (частость) появления j-го значения переменной Y.
Знак «-» в этой формуле означает, что прирост информации равен утраченной неопределенности (энтропии). Существуют специальные таблицы величин – 
, значительно упрощающие расчеты H(y).
|
|
|
Полная энтропия распределения переменной Y вычисляется на основе безусловного распределения.
После вычисления полной энтропии рассчитывается неопределенность распределения Y при закрепленном значении X, т. е. энтропия условного распределения Y:
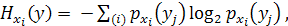(4. 2)
где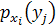 
= 
.
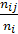Эта формула определяет энтропию распределения Y при i-м значении переменной X. Тогда условная энтропия определяется как:
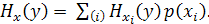(4. 3)
Если X полностью предопределяет распределение Y, то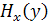 
= 0, т. е. знание переменной X полностью устраняет неопределенность наших знаний об Y. Если X не связан с Y, то = 
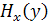Количество информации о переменной Y за счет знания переменной
X определяется как разность между полной и условной энтропией переменной Y:
I(y, x) = H(y) - Hx(y) (4. 4)
Иначе говоря, количество информации можно интерпретировать как уменьшение неопределенности признака Y за счет информации, полученной о связи X и Y. Показатель I(y, x) принимает значение, равное 0, если признаки Y и X статистически независимы. Максимальное значение I(y, x), равное H(y) или H(x), соответствует функциональной зависимости (полной связи) признаков Y и X, то есть когда каждому значению xi признака X соответствует единственное значение yi признака Y.
При анализе взаимосвязи признаков на основе взаимной информации I(y, x), в случае, когда таблица сопряженности базируется на выборочных данных, необходимо проверять значимость статистической зависимости, если I(y, x) отлично от 0. Для этого используется критерий 
. По таблице распределения для заданного уровня значимости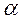 
, числа степеней свободы к = (m – 1)(p – 1) и объема выборки N определяется критическое значение Iкр. = / 2N. Затем это значение сравнивается с фактическим Iфакт. (y, x), и если Iкр > Iфакт. , то на заданном уровне значимости нет оснований отклонить гипотезу о независимости Y и X, в противном случае на заданном уровне значимости гипотеза о независимости признается неверной.
Существует целое семейство теоретико-информационных коэффициентов связи. Наиболее известным является коэффициент нормированной информации:
|
|
|
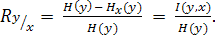(4. 5)
Этот показатель можно рассматривать как меру относительного уменьшения (редукции) неопределенности наших знаний об Y при получении знания об X. Коэффициент нормированной информации 
обладает следующими свойствами:
1) 0 ≤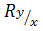 
≤ 1;
2) 
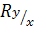= 0, если переменные независимы;
3) 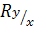= 1, если между Y и X имеет место полная (функциональная) связь;
4) 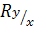инвариантен к перестановке местами строк и столбцов таблицы сопряженности;
По своей конструкции коэффициент нормированной информации аналогичен коэффициенту детерминации, т. е. его можно выражать в процентах. Применяя коэффициент нормированной информации, необходимо иметь ввиду, что если 
, то связь между переменными либо умеренно тесная, либо тесная.
Коэффициент нормированной информации является асимметричной мерой связи: 
Симметризованный коэффициент нормированной информации имеет вид:
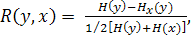(4. 6)
где H(x) – энтропия распределения по переменной X (для безусловного распределения).
Этот показатель имеет те же свойства, что и - коэффициент нормированной информации.
Симметризованный коэффициент нормированной информации может быть применен для оценки связи категоризированных данных, представленных в двумерной таблице сопряженности.
Пример 4. 1 . Изучается зависимость образования взрослых детей (сына или дочери) от образования родителей. С помощью теоретико-информационных коэффициентов связи необходимо выяснить, влияет ли образование родителей на образование детей.
Таблица 4. 1. Зависимость образования взрослых детей от образования родителей
| Образование родителей, х | Образование взрослых детей, у | Всего | |||
| Высшее | Среднее специаль ное | Общее среднее и неполное среднее | Итого | в % к итогу | |
| Высшее Среднее специальное Общее среднее Неполное среднее Начальное | 83, 5 42, 5 55, 0 26, 2 20, 2 | 10, 4 50, 5 25, 4 36, 9 29, 6 | 6, 1 7, 0 19, 6 36, 9 50, 2 | 12, 4 14, 8 16, 4 20, 6 35, 8 | |
| Итого | 38, 4 | 31, 1 | 30, 5 | ||
Решение: По данным таблицы вычислим полную энтропию переменной Y по безусловному распределению, т. е. по данным о распределении взрослых детей по уровню образования без учета образования родителей:
|
|
|
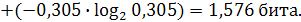
Характер итогового распределения указывает на то, что оно близко к равновероятному. Это означает, что полученное значение энтропии близко к максимальной неопределенности, т. е. к 
. Затем рассчитаем энтропии условных распределений детей по образованию при условии определенного образования родителей:
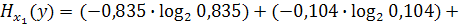
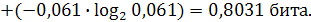
Точно так же рассчитываются значения энтропии других условных распределений детей по образованию:
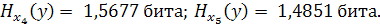
Сравнение полученных значений 
свидетельствует о влиянии образования родителей. Так, в первом случае при наличии высшего образования у родителей энтропия распределения детей наименьшая, т. е., если родители имеют высшее образование, то более вероятно, что дети также получат высшее образование.
Условная энтропия распределения детей по образованию вычисляется как средняя взвешенная из полученных значений :
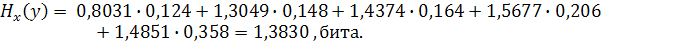
Данные об образовании родителей уменьшили неопределенность знания об образовании детей. Полученное количество информации составило:
I(y, x) = 1, 5767 – 1, 3830 = 0, 1937 бита.
Тогда коэффициент нормированной информации будет равен:
Такое значение коэффициента нормированной информации указывает на то, что связь либо умеренно тесная, либо тесная.
Поскольку по своему строению коэффициент нормированной информации аналогичен коэффициенту детерминации, то его можно выражать в процентах. В данном примере количество информации составляет 12, 3% энтропии распределения взрослых детей по уровню образования.
Вывод: Значения теоретико-информационных коэффициентов связи указывают на наличие зависимости между образованием взрослых детей и
образованием родителей: если у родителей есть высшее образование, то более вероятно, что взрослые дети также будут иметь высшее образование.
|
|
|
