 |
Градиент электрического потенциала и вектор Е. Силовые линии поля. Эквипотенциальные поверхности.
|
|
|
|
Градиент (потенциала) – вектор, показывающий направление наибольшего роста скалярной функции 
:
, (9)
где 
, 
– координатные орты.
Величина этого вектора равна изменению потенциала 
при перемещении на единицу длины в направлении быстрейшего изменения.
Длина градиента (потенциала) равна
. (10)
Из механики известно, что консервативная сила равна градиенту потенциальной энергии частицы, взятому с обратным знаком, т.е.
, (11)
где 
– символический вектор, называемый оператором Гамильтона или оператором набла.
Для электростатического поля имеем:
.
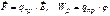Тогда соотношение (11) принимает вид
,
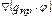или 
, (12)
т.е. напряженность электрического поля равна градиенту потенциала с обратным знаком.
Знак минус в (12) показывает, что вектор 
направлен противоположно вектору градиента потенциала 
, и силовые линии электрического поля являются линиями, вдоль которых потенциал изменяется наиболее быстро.
Очевидно, что проекция вектора 
на произвольное направление l равна со знаком минус частной производной потенциала по данному направлению:
. (13)
В случае однородного электрического поля (поля плоского конденсатора), в любой точке которого вектор напряженности 
постоянен как по величине, так и по направлению, имеем простое соотношение:
, (14)
где 
– разность потенциалов или напряжение между пластинами конденсатора (или между двумя эквипотенциальными поверхностями);
– расстояние между пластинами конденсатора (или между двумя эквипотенциальными поверхностями).
Поверхность, все точки которой имеют одинаковый потенциал, называется поверхностью равного потенциала или эквипотенциальной поверхностью, для которой
|
|
|
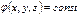. (15)
Перенос заряда вдоль эквипотенциальной поверхности не требует работы (разность потенциалов двух любых точек этой поверхности равна нулю). Это означает, что сила, действующая на переносимый заряд, перпендикулярна к перемещению.
Следовательно, вектор 
всегда направлен по нормали к эквипотенциальной поверхности, т.е. линии напряженности в каждой точке ортогональны к эквипотенциальной поверхности.
Итак, можно сделать важный вывод о том, что электрическое поле полностью можно описать векторной величиной – напряженностью . Но во многих случаях оказывается, что для вычисления напряженности 
электрического поля удобнее сначала определить потенциал φ и затем по формуле
вычислить напряженность 
.
Силовые линии — направленные линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности электрического поля. Отсюда следует, что напряженность 
равна разности потенциалов U на единицу длины силовой линии.
Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определить между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые линии – прямые. Поэтому здесь определить 
наиболее просто:
 .
| (3.6.1) |
Теперь дадим определение эквипотенциальной поверхности. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности
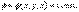
| (3.6.2) |
Графическое изображение силовых линий и эквипотенциальных поверхностей показано на рисунке 3.4.
Рис. 3.4
При перемещении по этой поверхности на d l потенциал не изменится: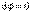 
Отсюда следует, что проекция вектора 
на d l равнанулю, то есть 
Следовательно, 
в каждой точке направлена по нормали к эквипотенциальной поверхности.
|
|
|
Эквипотенциальных поверхностей можно провести сколько угодно много. По густоте эквипотенциальных поверхностей можно судить о величине , это будет при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине
|
|
|
