Вынужденные колебания. Резонанс.

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.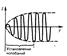

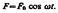
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к ча­стоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При 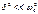значение w _рез практически совпадает с собственной частотой w ₀ колебательной системы.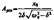

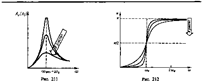
На рис. 211 представлены резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока) максимальна при w _рез =w ₀ и равна , т. е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой. что амплитуда скорости при механическом резонансе равна

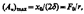
а амплитуда тока при электрическом резонансе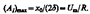

Зависимость j от w при разных коэффициентах d графически представлена на рис. 212, из которого следует, что при изменении w изменяется и сдвиг фаз j. Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.

 

 

Уравнение Максвелла. Интегральная и дифференциальная форма уравнений. Вектор Пойнтинга. Физический смысл уравнений Максвелла.

В основе теории Максвелла лежат рассмотренные выше четыре уравнения:

1. Электрическое поле может быть как потенциальным (Е _Q), так и вихревым (Е _B), поэтому напряженность суммарного поля Е = Е _Q + Е _B. Так как цир­куляция вектора Е _Q равна нулю, а циркуляция вектора Е _B определяется выражением, то циркуляция вектора напряженности суммарного поля

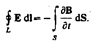
2. Обобщенная теорема о циркуляции вектора Н:

3. Теорема Гаусса для поля D:

(139.1)

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плот­ностью r, то формула запишется в виде

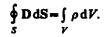
4. Теорема Гаусса для поля В:

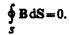
Итак, полная система уравнений Максвелла в интегральной форме:

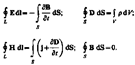
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):

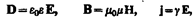
где e ₀ и m ₀ — соответственно электрическая и магнитная постоянные, e и m — соответст­венно диэлектрическая и магнитная проницаемости, g — удельная проводимость веще­ства.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Мак­свелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Для стационарных полей (E= const и B= const ) уравнения Максвелла примут вид

т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости. Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнении Максвелла в дифференциальном форме (характеризующих поле в каждой точке пространства):

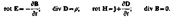
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла — интегральная и дифференциальная — эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Вектор Умова-Пойнтинга

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: