 |
Закон полного тока. Потенциальные и соленоидные векторные поля
|
|
|
|
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В):
циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m 0 на алгебраическую сумму токов, охватываемых этим контуром: 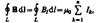 (118.1)
(118.1)
где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 173,

Выражение (118.1) справедливо только для поля в вакууме, поскольку, как будет показано ниже, для поля в веществе необходимо учитывать молекулярные токи.
Векторное поле а, поток к-го через любую кусочно-гладкую поверхность, лежащую в области G и являющуюся границей некоторой ограниченной области, равен нулю, называется соленоидальным в G.
Магнитное поле прямого тока, бесконечного соленоида, тороида.
Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины 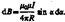 (110.4)
(110.4)
Так как угол a для всех элементов прямого тока изменяется в пределах от 0 до p, то, согласно (110.3) и (110.4),

Следовательно, магнитная индукция поля прямого тока

выражению для магнитной индукции поля внутри соленоида(в вакууме): 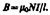 (119.2)
(119.2)
Получили, что поле внутри соленоида однородно
Важное значение для практики имеет также магнитное поле торонда — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 176). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.
|
|
|

Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции (118.1), B× 2p r=m 0 NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)

где N — число витков тороида.
Если контур проходит вне тороида, то токов он не охватывает и B× 2p r= 0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).
37.Дифференциальная форма основных законов магнитного поля. Дивергенция и ротор поля B.
Циркуляция вектора В магнитного поля не равна нулю. Такое поле называется вихревым.
дивергенция — это дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля.


Это же выражение можно записать с использованием оператора набла
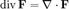
С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или стоком этого поля:
 — точка поля является источником;(в-во поступает в объем)
— точка поля является источником;(в-во поступает в объем)
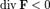 — точка поля является стоком;(удаляется из него)
— точка поля является стоком;(удаляется из него)
 — стоков и источников нет, либо они компенсируют друг друга.
— стоков и источников нет, либо они компенсируют друг друга.
Ротор векторного поля — вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру L плоской площадки ΔS, перпендикулярной к этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:  .
.
(а-циркуляция вектора по контуру а)
Ротор-векторная характеристика вращательной составляющей веторного поля(=вихрь)
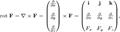
где i, j и k — единичные орты для осей x, y и z соответственно.
|
|
|


