 |
3. Законы управления. 5. Задачи ТАУ и характеристика процессов управления. 6. Математическое описание линейных САУ. Линеаризация. Формы записи ДУ.
|
|
|
|
3. ЗАКОНЫ УПРАВЛЕНИЯ
Зависимость U=F(E) – закон управления.
Пропорциональный П U=Kп*E
Интегральный И. U=Kи* 
Дифференциальный ПД. U=Kд*d(E(t))/dt
ПИ U=Kп*E+Kи*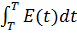 
ПИД. U=Kп*E+Kи* 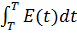+ Kд*d(E(t))/dt
ПИД закон является универсальным, остальные законы регулирования являются его частными случаями. Каждый закон имеет несколько модификаций.
Кп - коэффициент пропорциональности.
Кд – коэффициент дифференцирования
Ки – коэффициент интегрирования
T - время интегрирования.
5. Задачи ТАУ и характеристика процессов управления
Основные проблемы:
1. Информационная (сбор и обработка информации)
2. Устойчивость (свойство процессов САУ приходить в установившееся значение)
3. Качество процессов управления – комплекс показателей на процесс САУ близок к заданному
4. Оптимизация процессов управления
5. Параметры:
1) Наблюдаемость и измеримость
2) Управляемость – возможность перевода системы из одного в другое
3) Устойчивость
6. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЛИНЕЙНЫХ САУ. ЛИНЕАРИЗАЦИЯ. ФОРМЫ ЗАПИСИ ДУ.
2 основных способа получения математической модели:
1) аналитический
2) экспериментальный
Уравнение динамики и статики.
САУ и любой элемент производит преобразование входного x(t) и выходного y(t) сигнала.
А – оператор.
Математическая модель САУ может быть представлена в виде звеньев.
Звено - математическая модель системы или ее любой части определенная некоторым оператором. Например:
-уравнение динамики
У= выходная переменная, u, v –входные переменные.
Если входные воздействия постоянны, соответственно:
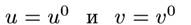то процесс установился.
Выходная переменная приобретает со временем постоянное значение.
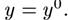- не ноль, а постоянное значение, или около положения равновесия.
|
|
|
Когда звено описывается ДУ, то у(t) зависит от предыстории (положение в начальный момент). Соответственно динамическое звено обладает динамическим запаздыванием. Если звено описывается функцией, то уравнение динамики равно уравнению статики. Статический режим может описать с помощью статических характеристик звена. Если связь между входной и выходной величиной однозначная, то звено называется статическим, иначе астатическим.
Линеаризация ДУ. Форма записи ДУ.
Линеаризация- построение из нелинейных упрощением линейной модели.
Почему возможна линеаризация:
1) САУ проектируют так чтобы реальный процесс отличался от требуемого режима, отклонения малы.
2) при больших отклонениях может потерять часть режимов.
Пусть в заданном режиме:
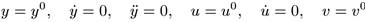
отклонения.
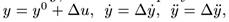
Подставим полученные значения в уравнение динамики и разложим функцию в ряд Тейлора получим:
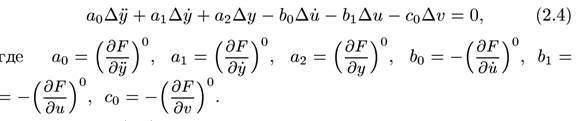(линейное ДУ в отклонениях).
Форма Коши: 
7. ОПЕРАТОРНАЯ ФОРМА ЗАПИСИ ЛИНЕЙНЫХ ДУ, ПЕРЕДАТОЧНЫЕ ФУНКЦИИ, СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
В классическом ТАУ принято записывать ТАУ в двух формах:
1) стандартная форма записи звена.
В уравнении 
откажемся от 
.
В стандартной форме сделаем, чтобы коэффициент при форме =1.
2) символическая (операторная) форма записи.
р - оператор дифференцирования.
собственный оператор, или характеристический поленом ДУ.
3) форма записи в пространстве состояний (A, B, C, D- форма)
U=A*u+B*x
y=C*U+D*x
A-матрица коэффициентов системы
B-матрица входных коэффициентов (матрица управления).
C- матрица выходного коэффициета.
D- матрица коэффициентов пропорциональности каналов.
обратное преобразование Лапласа.
Основные свойства преобразования Лапласа:
|
|
|
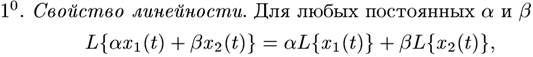
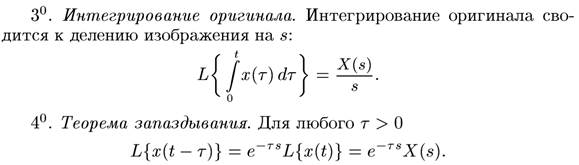
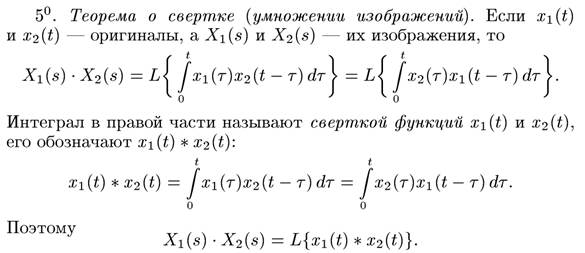
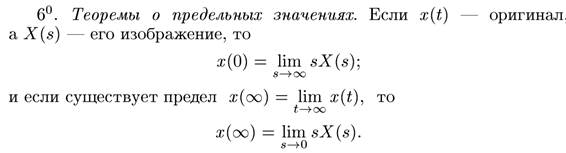
