6.2.5. Правила построения ЧХ элементарных звеньев

6. 2. 5. Правила построения ЧХ элементарных звеньев

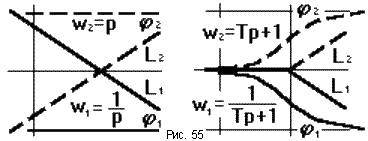При построении ЧХ некоторых звеньев можно использовать “правило зеркала”: при k = 1 ЛАЧХ и ЛФЧХ звеньев с обратными передаточными функциями зеркальны относительно горизонтальной оси. Так на рис. 55 изображены ЧХ идеального дифференцирующего и идеального форсирующего звеньев.

Если k 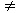1, то передаточную функцию звена можно рассматривать как произведениеW = k. W₁, где W₁ - передаточная функция с k = 1. При этом амплитуда вектора АФЧХ W(j ) при всех значениях должна быть увеличена в k раз, то есть A( ) = kA₁( ). Поэтому, например, центр полуокружности АФЧХ апериодического звена будет находиться не в точке P = 1/2, а в точке k/2. ЛАЧХ также изменится: L( ) = 20lgA( ) = 20lgkA₁( ) = 20lgk + 20lgA₁( ). Поэтому при k 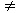1 ЛАЧХ звена нужно поднять по оси ординат не меняя ее формы на 20lgk. На ЛФЧХ изменение k никак не отразится. 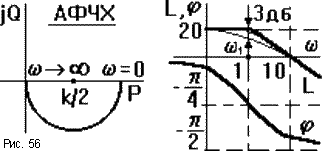Для примера на рис. 56 приведены частотные характеристики апериодического звена при k = 10 и T = 1c. При этом ЛАЧХ апериодического звена с k = 1 поднята вверх на 20lg10 = 20.

 

2. 4. 4. Частотные характеристики

 

Частотные характеристики описывают передаточные свойства элементов и АСУ в режиме установившихся гармонических колебаний, вызванных внешним гармоническим воздействием. Они находят применение в ТАУ, так как реальные возмущения, а следовательно и реакции на них элемента или АСУ могут быть представлены как сумма гармонических сигналов.

Рассмотрим сущность и разновидности частотных характеристик. Пусть на вход линейного элемента (рис. 2. 12, а) в момент времени t = 0  подано гармоническое воздействие с частотой w

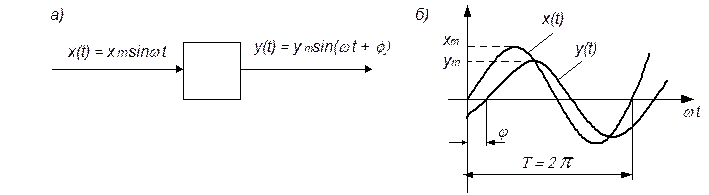
x(t) = x_m sinw t.                                                         (2. 32)

 

Рис. 2. 12. Схема и кривые, поясняющие сущность частотных характеристик

По завершении переходного процесса установится режим вынужденных колебаний и выходная величина y(t) будет изменяться по тому же закону, что и входная x(t), но в общем случае с другой амплитудой y_m и с фазовым сдвигом j по оси времени относительно входного сигнала (рис. 2. 12, б):

y(t) = y_m sin(w t + j ).                           (2. 33)

Проведя аналогичный опыт, но при другой частоте w, можно увидеть, что амплитуда y_m  и фазовый сдвиг j изменились, т. е. они зависят от частоты. Можно убедиться также, что для другого элемента зависимости параметров y_m и j от частоты w иные. Поэтому такие зависимости могут служить характеристиками динамических свойств элементов.

В ТАУ наиболее часто используют следующие частотные характеристики:

· амплитудная частотная характеристика (АЧХ);

· фазовая частотная характеристика (ФЧХ);

· амплитудно-фазовая частотная характеристика (АФЧХ).

Амплитудная частотная характеристика (АЧХ) – зависимость отношения амплитуд выходного и входного сигналов от частоты         

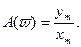(2. 34)

АЧХпоказывает, как элемент пропускает сигналы различной частоты. Пример АЧХ приведен на рис. 2. 13, а.   

 

Рис. 2. 13. Частотные характеристики:

а – амплитудная; б – фазовая; в – амплитудно-фазовая; г – логарифмическая

Фазовая частотная характеристика ФЧХ – зависимость фазового сдвига между входным и выходным сигналами от частоты.

ФЧХ показывает, какое отставание или опережение выходного сигнала по фазе создает элемент при различных частотах. Пример ФЧХ приведен на рис. 2. 13, б.

Амплитудную и фазовую характеристики можно объединить в одну общую – амплитудно-фазовую частотную характеристику (АФЧХ). АФЧХ представляет собой функцию комплексного переменного jw:

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: