 |
6.2. Частотные характеристики типовых звеньев
|
|
|
|
6. 2. Частотные характеристики типовых звеньев
Зная передаточную функцию звена W(p) легко получить все его частотные характеристики. Для этого необходимо подставить в нее j  вместо p, получим АФЧХ W(j
вместо p, получим АФЧХ W(j  ). Затем надо выразить из нее ВЧХ P(
). Затем надо выразить из нее ВЧХ P(  ) и МЧХ (Q(
) и МЧХ (Q(  ). После этого преобразуют АФЧХ в показательную форму и получают АЧХ A(
). После этого преобразуют АФЧХ в показательную форму и получают АЧХ A(  ) и ФЧХ
) и ФЧХ  (
(  ), а затем определяют выражение ЛАЧХ L(w) = 20lgA(
), а затем определяют выражение ЛАЧХ L(w) = 20lgA(  ) (ЛФЧХ отличается от ФЧХ только масштабом оси абсцисс).
) (ЛФЧХ отличается от ФЧХ только масштабом оси абсцисс).
6. 2. 1. Безынерционное звено
 Передаточная функция:
Передаточная функция:
W(p) = k.
АФЧХ: W(j  ) = k.
) = k.
ВЧХ: P(  ) = k.
) = k.
МЧХ: Q(  ) = 0.
) = 0.
АЧХ: A(  ) = k.
) = k.
ФЧХ:  (
(  ) = 0.
) = 0.
ЛАЧХ: L(  ) = 20lgk.
) = 20lgk.
Некоторые ЧХ показаны на рис. 50. Звено пропускает все частоты одинаково c увеличением амплитуды в k раз и без сдвига по фазе.
6. 2. 2. Интегрирующее звено
 Передаточная функция:
Передаточная функция:
W(p) = k/p.
Рассмотрим частный случай, когда k = 1, то есть
W(p) = 1/p.
АФЧХ: W(j  ) =
) =  .
.
ВЧХ: P(  ) = 0.
) = 0.
МЧХ: Q(  ) = - 1/
) = - 1/  .
.
АЧХ: A(  ) = 1/
) = 1/  .
.
ФЧХ:  (
(  ) = -
) = -  /2.
/2.
ЛАЧХ: L(  ) = 20lg(1/
) = 20lg(1/  ) = - 20lg(
) = - 20lg(  ).
).
ЧХ показаны на рис. 51. Все частоты звено пропускает с запаздыванием по фазе на 90о. Амплитуда выходного сигнала увеличивается при уменьшении частоты, и уменьшается до нуля при росте частоты (звено " заваливает" высокие частоты). ЛАЧХ представляет собой прямую, проходящую через точку L(  ) = 0 при
) = 0 при  = 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен – 20 дб/дек (децибел на декаду).
= 1. При увеличении частоты на декаду ордината уменьшается на 20lg10 = 20дб, то есть наклон ЛАЧХ равен – 20 дб/дек (децибел на декаду).
6. 2. 3. Апериодическое звено
 При k = 1 получаем следующие выражения ЧХ:
При k = 1 получаем следующие выражения ЧХ:
W(p) =  ;
;
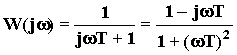 ;
;
 ;
;
 ;
;
 (
(  ) =
) =  1 -
1 -  2 = - arctg(
2 = - arctg(  T);
T);
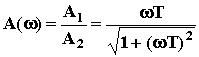 ;
;
L(  ) = 20lg(A(
) = 20lg(A(  )) = - 10lg(1 + (
)) = - 10lg(1 + (  T)2).
T)2).
Здесь A1 и A2 - амплитуды числителя и знаменателя ЛФЧХ;  1 и
1 и  2 - аргументы числителя и знаменателя. ЛФЧХ:
2 - аргументы числителя и знаменателя. ЛФЧХ:
ЧХ показаны на рис. 52. АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2. При построении асимптотической ЛАЧХ считают, что при  <
<  1 = 1/T можно пренебречь (
1 = 1/T можно пренебречь (  T)2 выражении для L(
T)2 выражении для L(  ), то есть L(
), то есть L(  )
)  - 10lg1 = 0.. При
- 10lg1 = 0.. При  >
>  1 пренебрегают единицей в выражении в скобках, то есть L(w)
1 пренебрегают единицей в выражении в скобках, то есть L(w)  - 20lg(wT). Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота w1 называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при
- 20lg(wT). Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота w1 называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при  =
=  1.
1.
|
|
|
ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к -  /2 при возрастании
/2 при возрастании  до бесконечности. Перегиб в точке
до бесконечности. Перегиб в точке  =
=  1 при
1 при  (
(  ) = -
) = -  /4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.
/4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.
6. 2. 4. Инерционные звенья второго порядка
При k = 1 передаточная функция звена: W(p) =  .
.
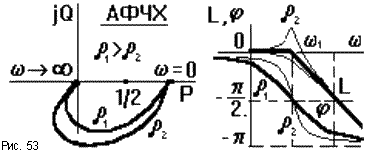 В виду сложности вывода выражений для частотных характеристик рассмотрим их без доказательства, они показаны на рис. 53.
В виду сложности вывода выражений для частотных характеристик рассмотрим их без доказательства, они показаны на рис. 53.
Асимптотическая ЛАЧХ колебательного звена до сопрягающей частоты  1 = 1/T1 совпадает с осью абсцисс, при дальнейшем увеличении частоты идет с наклоном - 40 дб/дек. То есть высокие частоты колебательное звено " заваливает" сильнее, чем апериодическое звено.
1 = 1/T1 совпадает с осью абсцисс, при дальнейшем увеличении частоты идет с наклоном - 40 дб/дек. То есть высокие частоты колебательное звено " заваливает" сильнее, чем апериодическое звено.
Реальная ЛАЧХ при 

 1 значительно отличается от асимптотической. Это отличие тем существенней, чем меньше коэффициент демпфирования
1 значительно отличается от асимптотической. Это отличие тем существенней, чем меньше коэффициент демпфирования 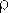 . Точную кривую можно построить, воспользовавшись кривыми отклонений, которые приводятся в справочниках. В предельном случае
. Точную кривую можно построить, воспользовавшись кривыми отклонений, которые приводятся в справочниках. В предельном случае  = 0 получаем консервативное звено, у которого при
= 0 получаем консервативное звено, у которого при 

 1 амплитуда выходных колебаний стремится к бесконечности (рис. 54).
1 амплитуда выходных колебаний стремится к бесконечности (рис. 54). 
ЛФЧХ при малых частотах асимтотически стремится к нулю. При увеличении частоты до бесконечности выходной сигнал поворачивается по фазе относительно входного на угол, стремящийся в пределе к - 180о. ЛФЧХ можно построить с помощью шаблона, но для этого нужен набор шаблонов для разных коэффициентов демпфирования. При уменьшении коэффициента демпфирования АФЧХ приближается к оси абсцисс и в пределе у консервативного звена она вырождается в два луча по оси абсцисс, при этом фаза выходных колебаний скачком меняется от нуля до - 180о при переходе через сопрягающую частоту (рис. 54).
|
|
|
|
|
|


