 |
11. Позиционные звенья и их характеристики
|
|
|
|
Минимально-фазовые элементы дают минимальный фазовый сдвиг j (w) по сравнению с любыми другими элементами, имеющими такую же амплитудную характеристику A(w ), но у которой действительная часть хотя бы одного полюса или нуля положительна.
Минимально-фазовые элементы обладают важным для практических расчетов свойством: их частотная передаточная функция полностью определяется одной из трех составляющих - A(w ), P(w ) и Q(w ). Это существенно упрощает задачи анализа и синтеза минимально-фазовых систем.
11. Позиционные звенья и их характеристики
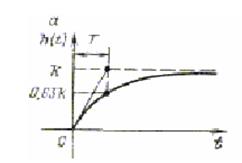
Примерами технической реализации звена являются механический редуктор, потенциометрический датчик углового перемещения, тахогенератор, операционный усилитель. Понятие безынерционного звена является продуктом математической идеализации. На самом деле все реальные конструктивные элементы обладают некоторой инерционностью, так как передача энергии со входа на выход не может осуществляться мгновенно.
12 ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ
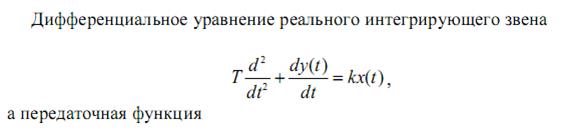
13. ДИФФЕРЕНЦИРУЮЩИЕ ЗВЕНЬЯ
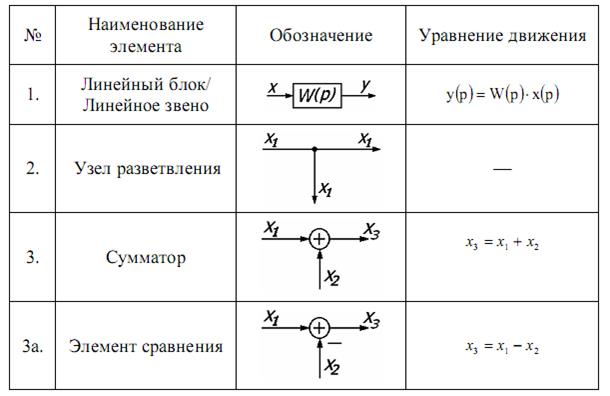
14. СТРУКТУРНЫЕ СХЕМЫ И ПРАВИЛА ИХ ПРЕОБРАЗОВАНИЯ
15. ПОНЯТИЕ УСТОЙЧИВОСТИ САУ. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ
Понятие устойчивости системы
Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.
Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы (рис. 61). Говорят, что система устойчива " в малом", если определен факт наличия устойчивости, но не определены ее границы. Система устойчива " в большом", когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы.
|
|
|
В соответствии с классическим методом решение дифференциального уравнения ищется в виде: Y(t) = Yвын(t) + Yсв(t).
Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. yвын(t) - частное решение неоднородного дифференциального уравнения, под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t). Поэтому вторая составляющая общего решения называется вынужденный. Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.
16. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
Необходимое условие устойчивости
Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде
D(p) = aopn + a1pn-1 + a2pn-2 +... + an = ao(p-p1)(p-p2)... (p-pn) = 0,
где p1, p2, ..., pn - корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней отрицательны, что можно записать как ai = -|ai| < 0. Подставим их в уравнение:
a0 (p + |a1|) (p + |a2| - j 2) (p + |a2| + j 2)... = 0.
Перемножая комплексно сопряженные выражения, получим:
a0 (p + |a1|) ((p + |a2|)2 + ( 2)2)... = 0.
После раскрытия скобок должно получиться выражение
|
|
|
