21.  метод фазовой плоскости. Особые точки и их типы.

21.  МЕТОД ФАЗОВОЙ ПЛОСКОСТИ. ОСОБЫЕ ТОЧКИ И ИХ ТИПЫ.

 

Метод фазовой плоскости — графоаналитический метод исследования динамических систем, приводимых к уравнениям вида:

Теоретические основы метода разработаны Пуанкаре и Ляпуновым, однако метод систематически не использовался до 1930х годов.

Обычно метод применяется для исследования нелинейных систем, в случаях, когда линеаризация приводит к неудовлетворительным ошибкам, либо когда линеаризация значительно ограничена в применимости по времени.

С помощью метода находят характеристики особых точек, изолированных замкнутых траекторий и сепаратрис, что в свою очередь позволяет оценить динамику разрабатываемой или исследуемой нелинейной динамической системы в широком диапазоне возможных начальных условий.

На рис. Фазовый портрет системы, устойчивой в большом, и неустойчивой в малом. Эллипс выделенный жирным — устойчивый предельный цикл, характеризующий автоколебания, и в данном случае являющейся сепаратрисой.

Особые точки и их типы.

 

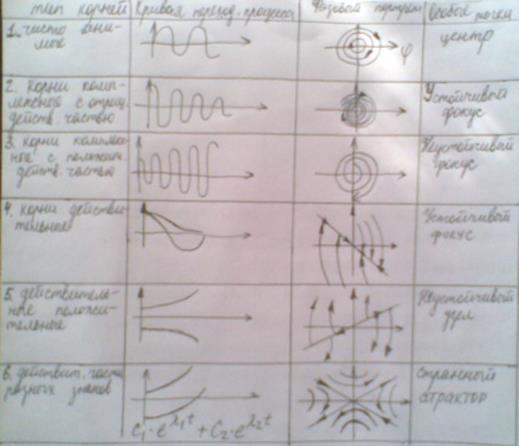
22. МЕТОД ПРИПАСОВЫВАНИЯ

Метод припасовывания

Часто нелинейные системы представляются как кусочно-линейные, т. е. их динамические свойства описываются линейными дифференциальными уравнениями, разными для разных участков процесса управления.

Метод припасовывания состоит в том, что линейные дифференциальные уравнения решаются в общем виде отдельно для каждого участка процесса, на котором они справедливы. Затем на каждом участке в полученных решениях произвольные постоянные определяются таким образом, чтобы все соседние участки правильно состыко­вывались друг с другом. Это делается следующим обра­зом: по заданным начальным условиям процесса определяются произвольные постоянные в общем решении для первого участка. Значения фазовых координат в конце первого участка служат начальными условиями для вто­рого участка и т. д.

Вообще говоря, описанная схема метода припасовывания может быть применена и тогда, когда какой-либо участок описывается нелинейным дифференциальным уравнением при условии, что известно его общее решение.

Проиллюстрируем на простом примере использование метода припасовывания для определения переходного процесса и для определения периодического решения (автоколебаний). Дана система, схема которой изображена на рис. 3. 1, а, нелинейная характеристика Р(х) регулятора представлена на рис. 3. 1б. Уравнение объекта: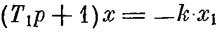

уравнение регулятора:

Общее уравнение замкнутой системы имеет вид:

Определение переходного процесса. Представим себе примерно возможный качественный вид процесса:

(рис. 3. 2). Он разбивается на участки АВ, ВD и т. д., внутри которых в соответствии с нелинейной характеристикой функция Р(х) принимает постоянные значения +с или —с. Изобразим отдельно участки АВ и ВD (рис. 3. 3), отсчитывая время t на каждом из них от нуля.

На участке АВ: 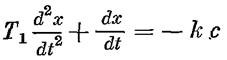, имеет интеграл в виде , второй

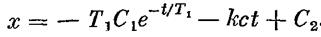
начальные условия: , по ним находим

На участке BD: 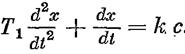, интеграл первый 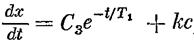, второй

Начальные условия для BD: , получаем .

На след. за точкой D снова будет решаться уравнение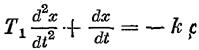

 

23.   МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ

Пусть входной сигнал нелинейного звена изменяется по гармоническому закону

х(t) = А sinω t(10. 8). Выходной сигнал

у(t) = Ф(А sinω t) будет периодической функцией времени, которую можно разложить в ряд Фурье. Первая гармоника этого ряда запишется в таком виде

(10. 10), где -коэффициенты гармонической линеаризации определяются по формулам:

Выражения (10. 11) показывают, что коэффициенты гармонической линеаризации зависят от амплитуды входного сигнала. Как известно, коэффициенты линеаризации в формуле (10. 10), найденные из разложения в ряд (10. 11), обеспечивают наилучшее квадратичное приближение гармонического сигнала y(t) к периодической кривой (10. 9)

Выражение (10. 10) можно представить и в другой форме (10. 13), где 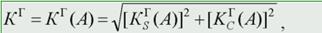 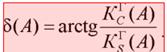Если перейти к комплексному виду записи уравнений (10. 8), (10. 10), (10. 13), то будем иметь: , где 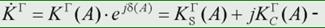 комплексный коэффициент гармонической линеаризации. Этот коэффициент, равный отношению  называют также гармоническим коэффициентом передачи (амплитудно-фазовой характеристикой) нелинейного звена, но, в отличие от последнего коэффициента  не зависит от частоты входного сигнала.

Модуль ( 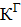) и фаза (δ ) этого коэффициента являются функцией только амплитуды (А) входного сигнала.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: