 |
Задачи для самостоятельного решения
|
|
|
|
У компании появилась вакантная должность на место главного бухгалтера. На данную должность выдвинуты три кандидатуры. Выбор кандидата осуществляется на основе трех критериев (компетентность, опыт работы и организаторские способности). Пусть даны некоторые экспертные оценки критериев (К1,К2,К3) и оценки кандидатов на должность (А1,А2,А3) по каждому из критериев определенные двумя экспертами (Э1,Э2) с различным уровнем компетентности. Определить специалиста, наиболее подходящего для данную должность.
Вариант 1
Оценки критериев
| К 1 | К 2 | К 3 | |
| К 1 | 1,5 | 0,5 | |
| К 2 | 0,5 | 1,5 | |
| К 3 | 1,5 | 0,5 |
Оценки уровня компетентности экспертов
| Э 1 | Э 2 | |
| Э 1 | ||
| Э 2 |
Оценки альтернатив по первому критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 1,5 | ||
| А 2 | 0,5 | ||
| А 3 |
Оценки альтернатив по первому критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | 0,5 | |
| А 2 | 1,5 | ||
| А 3 | 1,5 |
Оценки альтернатив по второму критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | ||
| А 2 | 1,5 | 0,5 | |
| А 3 | 1,5 |
Оценки альтернатив по второму критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | |||
| А 2 | 1,5 | ||
| А 3 | 0,5 |
Оценки альтернатив по третьему критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | 1,5 | |
| А 2 | 1,5 | 1,5 | |
| А 3 | 0,5 | 0,5 |
Оценки альтернатив по третьему критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | ||
| А 2 | 1,5 | 1,5 | |
| А 3 | 0,5 |
Вариант 2
Оценки критериев
| К 1 | К 2 | К 3 | |
| К 1 | 1,5 | 0,5 | |
| К 2 | 0,5 | 0,5 | |
| К 3 | 1,5 | 1,5 |
|
|
|
Оценки уровня компетентности экспертов
| Э 1 | Э 2 | |
| Э 1 | 0,5 | |
| Э 2 | 1,5 |
Оценки альтернатив по первому критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | 1,5 | |
| А 2 | 1,5 | 0,5 | |
| А 3 | 0,5 | 1,5 |
Оценки альтернатив по первому критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 1,5 | 1,5 | |
| А 2 | 0,5 | ||
| А 3 | 0,5 |
Оценки альтернатив по второму критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | ||
| А 2 | 0,5 | ||
| А 3 | 1,5 | 1,5 |
Оценки альтернатив по второму критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | 0,5 | |
| А 2 | 1,5 | 1,5 | |
| А 3 | 1,5 | 0,5 |
Оценки альтернатив по третьему критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 1,5 | 1,5 | |
| А 2 | 0,5 | ||
| А 3 | 0,5 |
Оценки альтернатив по третьему критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 1,5 | ||
| А 2 | 0,5 | 0,5 | |
| А 3 | 1,5 |
Вариант 3
Оценки критериев
| К 1 | К 2 | К 3 | |
| К 1 | 1,5 | 0,5 | |
| К 2 | 0,5 | 0,5 | |
| К 3 | 1,5 | 1,5 |
Оценки уровня компетентности экспертов
| Э 1 | Э 2 | |
| Э 1 | 1,5 | |
| Э 2 | 0,5 |
Оценки альтернатив по первому критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 1,5 | 1,5 | |
| А 2 | 0,5 | 1,5 | |
| А 3 | 0,5 | 0,5 |
Оценки альтернатив по первому критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | ||
| А 2 | |||
| А 3 | 1,5 |
Оценки альтернатив по второму критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | 0,5 | |
| А 2 | 1,5 | 0,5 | |
| А 3 | 1,5 | 1,5 |
Оценки альтернатив по второму критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 1,5 | ||
| А 2 | |||
| А 3 | 0,5 |
Оценки альтернатив по третьему критерию, данные первым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 1,5 | ||
| А 2 | 0,5 | 1,5 | |
| А 3 | 0,5 |
|
|
|
Оценки альтернатив по третьему критерию, данные вторым экспертом
| А 1 | А 2 | А 3 | |
| А 1 | 0,5 | ||
| А 2 | 1,5 | 1,5 | |
| А 3 | 0,5 |
Лабораторная работа №3
Метод анализа иерархий
Цель работы: Познакомиться с методом анализа иерархий и выполнить необходимые расчеты в программе Mathcad согласно определенному преподавателем варианту. Сделать выводы о решениях экспертов.
Теоретические сведения
Метод анализа иерархий (analytic hierarchy process) – это один из методов экспертных оценок, основанный на иерархическом представлении решаемой проблемы. В основе положен ранее рассмотренный метод парных сравнений.
Весь алгоритм метода сводится к нескольким этапам:
1. Определение цели, критериев и альтернатив, необходимых для решения поставленной задачи.
2. Построение иерархической модели задачи.
3. Опрос экспертов для построения матриц парных сравнений.
4. Обработать полученные результаты.
5. Анализ согласованности экспертных оценок.
Рассмотрим алгоритм метода анализа иерархий на примере.
Компания предполагает расширить торговую сеть за счет открытия новых магазинов за границей. Как варианты для рассмотрения выступают четыре страны (А1-А4).
1. Выбор осуществляется на основании трех критериев: политическая обстановка (К1), уровень жизни (К2) и состояние налогового законодательства (К3). Соответственно цель – выбор страны, в которой условия можно считать наиболее приемлемыми для ведения бизнеса.
2. На основе полученных результатов можно построить иерархическую структуру задачи, представленную на рисунке 4.
Рисунок 4 – Иерархическая структура задачи.
3. Далее проводится опрос экспертов, на основе мнения который составляются матрицы парных сравнений. Первоначально эксперты определяются приоритеты критериев, т.е. численное выражение важности каждого критерия. Томасом Саати была предложена девятибалльная шкала, представленная в таблице 13.
Таблица 13 – Шкала Саати
| Позиция шкалы | Определение |
| Равная важность | |
| Умеренное превосходство одного над другим | |
| Существенное или сильное превосходство | |
| Значительное превосходство | |
| Очень сильное превосходство | |
| 2,4,6,8 | Промежуточные решения между двумя соседними суждениями |
| Обратные величины приведенных выше чисел | Если при сравнении одного вида деятельности получили определенное значение, то при сравнении второго вида деятельности мы получим обратное значение (aij = 1/aji). |
|
|
|
Итак, экспертами были даны оценки степени важности критериев, представленные в виде таблицы 14.
Таблица 14 – Оценки важности критериев
| К 1 | К 2 | К 3 | |
| К 1 | |||
| К 2 | |||
| К 3 | 1/7 | 1/8 |
Далее необходимо получить оценки важности альтернатив по каждому из критериев. Итак, оценки распределились следующим образом.
Таблица 15 – Оценки важности альтернатив по критерию «Политическая обстановка»
| А 1 | А 2 | А 3 | А 4 | |
| А 1 | ||||
| А 2 | 1/4 | 1/4 | 1/7 | |
| А 3 | ||||
| А 4 | 1/3 | 1/5 |
Таблица 16 – Оценки важности альтернатив по критерию «Уровень жизни»
| А 1 | А 2 | А 3 | А 4 | |
| А 1 | ||||
| А 2 | 1/2 | |||
| А 3 | ½ | |||
| А 4 | 1/7 | 1/9 |
Таблица 17 – Оценки важности альтернатив по критерию «Налоговое законодательство»
| А 1 | А 2 | А 3 | А 4 | |
| А 1 | 1/2 | |||
| А 2 | ||||
| А 3 | 1/2 | |||
| А 4 | 1/3 | 1/8 | 1/6 |
Полученные матрицы это обратносимметричные матрицы следующего вида:
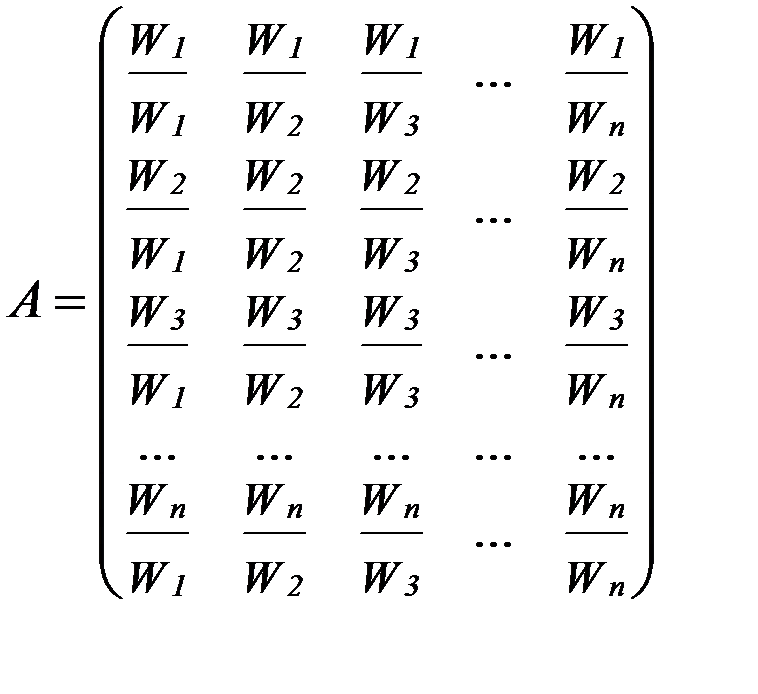
4. Для каждой полученной матрицы парных сравнений рассчитывается вектор приоритетов. Для этого вычисляется среднее геометрическое значение строки каждой матрицы, другими словами вычисляется оценка компоненты собственного вектора по формуле (1)
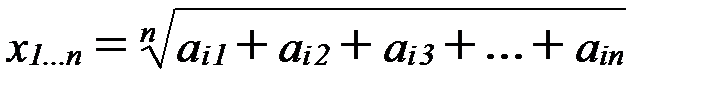 (1)
(1)
Где x1…n – оценки компонент собственного вектора,
ai1, ai2, ai3… ain – оценки экспертов для i-ого критерия или альтернативы,
n – число критериев или альтернатив.
После, каждое полученное значение делиться на сумму всех значений строк. Таким образом, мы получим локальные приоритеты или вектор приоритетов. В общем виде значение компонент вектора приоритетов можно рассчитать по формуле (2)
 (2)
(2)
Где L1…n – локальные приоритеты.
Примем приоритет критерия за «F», приоритет объекта по критерию за «T». Результаты расчетов вектора приоритетов критериев приведены в таблице 18.
|
|
|
Таблица 18 – Расчет локальных приоритетов критериев
| Наименование критерия | Оценки компонент собственного вектора критерия | Локальные приоритеты критериев (F j) |
| Политическая обстановка | 1,913 | 0,458 |
| Уровень жизни | 0,479 | |
| Налоговое законодательство | 0,261 | 0,063 |
В таблице 19 приведены результаты расчета приоритетов объектов по критерию.
Таблица 19 – Расчет локальных приоритетов объектов по критериям
| Альтернатива | Политическая обстановка | Уровень жизни | Налоговое законодательство | |||
| Оценки компонент собственного вектора альтернативы по критерию | Локальные приоритеты альтернативы по критерию (T i1) | Оценки компонент собственного вектора альтернативы по критерию | Локальные приоритеты альтернативы по критерию (T i2) | Оценки компонент собственного вектора альтернативы по критерию | Локальные приоритеты альтернативы по критерию (T i3) | |
| Страна 1 | 1,861 | 0,364 | 1,934 | 0,398 | 1,107 | 0,217 |
| Страна 2 | 0,307 | 0,06 | 1,732 | 0,356 | 2,378 | 0,467 |
| Страна 3 | 2,115 | 0,414 | 0,841 | 0,173 | 1,316 | 0,259 |
| Страна 4 | 0,827 | 0,162 | 0,355 | 0,073 | 0,284 | 0,057 |
Далее необходимо рассчитать глобальные приоритеты. Для этого необходимо матрицу, состоящую из векторов приоритетов альтернатив по критерию умножить на вектор приоритетов критериев. Расчеты осуществляются на основе следующей формулы (3)
 (3)
(3)
Где Gi – глобальные приоритеты альтернатив,
Fj – локальный приоритет критерия j,
Tij – локальный приоритет альтернативы i по критерию j.
Рассчитаем глобальные приоритеты стран:
G Страна 1 = 0,458*0,364+0,479*0,398+0,063*0,217 = 0,371
G Страна 2 = 0,458*0,06+0,479*0,356+0,063*0,467 = 0,228
G Страна 3 = 0,458*0,414+0,479*0,173+0,063*0,259 = 0,289
G Страна 4 = 0,458*0,162+0,479*0,073+0,063*0,057 = 0,113
По результатам расчетов можно сказать, что наилучшей для открытия торговой сети, по мнению экспертов, является страна под номером 1, с глобальным приоритетом 0,371.
5. Рассмотрим теперь этап анализа согласованности экспертных оценок. Если эксперт считает, что первый критерии превосходит как второй, так и третий критерии в два раза, то это не значит что для него второй и третий равны по важности. Суждения могут быть и иными. Чтобы оценить, насколько суждения эксперта верны, Саати предложил следующий метод. Изначально вычисляется λ max – наибольшее собственное значение матрицы суждений. Для этого суммируется произведения суммы элементов столбца на значение локальных приоритетов строк. Далее рассчитывается индекс согласованности по формуле (4)
 (4)
(4)
Где ИС – индекс согласованности,
λmax – наибольшее собственное значение матрицы суждений,
n – число сравниваемы элементов.
Расчет отношения согласованности осуществляется по формуле (5)
|
|
|
 (5)
(5)
Где ОС – отношение согласованности;
СС – случайная согласованность.
Автор метода привел следующие значения случайной согласованности, полученные на основе вероятностны измерений, представленные в таблице 20.
Таблица 20 – Значения случайной согласованности для матриц с определенным числом сравниваемых элементов
| Размер матрицы | ||||||||||
| Случайная согласованность | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
Отношение согласованности не должно превышать 0,1. В крайнем случае, это значение может быть 0,2.
Рассчитав отношение согласованности для матриц из нашего примера, получили следующие результаты.
Таблица 21 – Оценка согласованности матриц
| Наименование матрицы | λ max | ИС | ОС |
| Оценки важности критериев | 3,002 | 0,0009908 | 0,001708 |
| Оценки важности альтернатив по критерию «Политическая обстановка» | 4,396 | 0,132 | 0,147 |
| Оценки важности альтернатив по критерию «Уровень жизни» | 4,517 | 0,172 | 0,191 |
| Оценки важности альтернатив по критерию «Налоговое законодательство» | 4,033 | 0,011 | 0,012 |
Сильная сторона рассмотренного метода – прежде всего универсальность. Метод не ограничен областью применения. В то же время он прост в реализации, не требует особых знаний в области математики.
|
|
|


