 |
Тема 2. 3. Проверка существенности факторов и показатели качества регрессии
|
|
|
|
Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации.
Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.
Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
 ,
,
где
 – общая дисперсия результативного признака;
– общая дисперсия результативного признака;
 – остаточная дисперсия.
– остаточная дисперсия.
Границы изменения индекса множественной корреляции от 0 до 1.
Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов.
Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:
 .
.
При правильном включении факторов в регрессионную модель величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости.
Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках).
Отсюда ясно, что сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.
Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:
 .
.
Можно пользоваться следующей формулой индекса множественной детерминации:
|
|
|
 .
.
При линейной зависимости признаков формула индекса множественной корреляции может быть представлена следующим выражением:
 ,
,
где
 – стандартизованные коэффициенты регрессии;
– стандартизованные коэффициенты регрессии;
 – парные коэффициенты корреляции результата с каждым фактором.
– парные коэффициенты корреляции результата с каждым фактором.
Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции.
Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:
 ,
,
где

– определитель матрицы парных коэффициентов корреляции;

– определитель матрицы межфакторной корреляции.
Как видим, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции.
Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений  .
.
Если число параметров при  равно
равно  и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом.
и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом.
Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.
Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов
|
|
|

делится на число степеней свободы остаточной вариации
 ,
,
а общая сумма квадратов отклонений

на число степеней свободы в целом по совокупности
 .
.
Формула скорректированного индекса множественной детерминации имеет вид:
 ,
,
где
 – число параметров при переменных
– число параметров при переменных 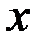 ;
;
 – число наблюдений.
– число наблюдений.
Поскольку
 ,
,
то величину скорректированного индекса детерминации можно представить в виде:
 .
.
Чем больше величина  , тем сильнее различия
, тем сильнее различия  и
и  .
.
Как было показано выше, ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( -коэффициенты).
-коэффициенты).
Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей).
Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции.
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
В общем виде при наличии  факторов для уравнения
факторов для уравнения

коэффициент частной корреляции, измеряющий влияние на 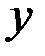 фактора
фактора  , при неизменном уровне других факторов, можно определить по формуле:
, при неизменном уровне других факторов, можно определить по формуле:
 ,
,
где
 – множественный коэффициент детерминации всех
– множественный коэффициент детерминации всех  факторов с результатом;
факторов с результатом;
 – тот же показатель детерминации, но без введения в модель фактора
– тот же показатель детерминации, но без введения в модель фактора  .
.
При двух факторах формула примет вид:
 ;
;
 .
.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается.
Например,  – коэффициент частной корреляции первого порядка.
– коэффициент частной корреляции первого порядка.
Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка.
Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:
|
|
|
 .
.
При двух факторах данная формула примет вид:
 ;
;
 .
.
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка.
Так, по уравнению

возможно исчисление трех частных коэффициентов корреляции второго порядка:
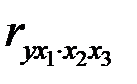 ,
,  ,
,  ,
,
каждый из которых определяется по рекуррентной формуле.
Например, при  имеем формулу для расчета
имеем формулу для расчета 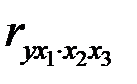 :
:
 .
.
Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1.
Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом.
Частные коэффициенты корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде.
Если из стандартизованного уравнения регрессии

следует, что
 ,
,
т.е. no силе влияния на результат порядок факторов таков:  ,
,  ,
,  , то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции,
, то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции,
 .
.
В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения.
Их используют на стадии формирования модели.
Так, строя многофакторную модель, на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции.
На втором шаге отбирается фактор с наименьшей и несущественной по  -критерию Стьюдента величиной показателя частной корреляции.
-критерию Стьюдента величиной показателя частной корреляции.
Исключив его из модели, строится новое уравнение регрессии.
Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля.
Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построения регрессионной модели почти не отличаются друг от друга,  , где
, где  – число факторов.
– число факторов.
Из приведенных выше формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции.
|
|
|
Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле:
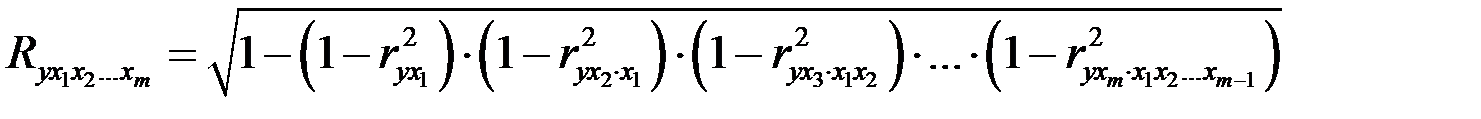 .
.
В частности, для двухфакторного уравнения формула принимает вид:
 .
.
При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице.
Из единицы вычитается доля остаточной вариации результативного признака
 ,
,
обусловленная последовательно включенными в анализ факторами.
В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью  -критерия Фишера:
-критерия Фишера:
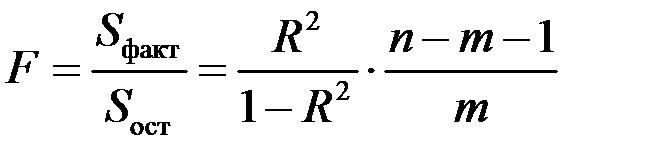 ,
,
где
 – факторная сумма квадратов на одну степень свободы;
– факторная сумма квадратов на одну степень свободы;
 – остаточная сумма квадратов на одну степень свободы;
– остаточная сумма квадратов на одну степень свободы;
 – коэффициент (индекс) множественной детерминации;
– коэффициент (индекс) множественной детерминации;
 – число параметров при переменных
– число параметров при переменных 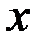 (в линейной регрессии совпадает с числом включенных в модель факторов);
(в линейной регрессии совпадает с числом включенных в модель факторов);
 – число наблюдений.
– число наблюдений.
Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель.
Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака.
Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности.
Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель.
Мерой для оценки включения фактора в модель служит частный  -критерий, т.е.
-критерий, т.е.  .
.
Частный  -критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом.
-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом.
В общем виде для фактора  частный
частный  -критерий определится как
-критерий определится как
 ,
,
где
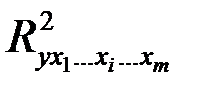 – коэффициент множественной детерминации для модели с полным набором факторов,
– коэффициент множественной детерминации для модели с полным набором факторов,
 – тот же показатель, но без включения в модель фактора
– тот же показатель, но без включения в модель фактора  ,
,
 – число наблюдений,
– число наблюдений,
 – число параметров в модели (без свободного члена).
– число параметров в модели (без свободного члена).
Фактическое значение частного  -критерия сравнивается с табличным при уровне значимости
-критерия сравнивается с табличным при уровне значимости  и числе степеней свободы: 1 и
и числе степеней свободы: 1 и  .
.
Если фактическое значение  превышает
превышает 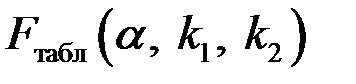 , то дополнительное включение фактора
, то дополнительное включение фактора  в модель статистически оправданно и коэффициент чистой регрессии
в модель статистически оправданно и коэффициент чистой регрессии  при факторе
при факторе  статистически значим.
статистически значим.
Если же фактическое значение  меньше табличного, то дополнительное включение в модель фактора
меньше табличного, то дополнительное включение в модель фактора  не увеличивает существенно долю объясненной вариации признака
не увеличивает существенно долю объясненной вариации признака 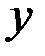 , следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.
, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.
|
|
|
Для двухфакторного уравнения частные  -критерии имеют вид:
-критерии имеют вид:
 ,
,
 .
.
С помощью частного  -критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор
-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор  вводился в уравнение множественной регрессии последним.
вводился в уравнение множественной регрессии последним.
Частный  -критерий оценивает значимость коэффициентов чистой регрессии.
-критерий оценивает значимость коэффициентов чистой регрессии.
Зная величину  , можно определить и
, можно определить и  -критерий для коэффициента регрессии при
-критерий для коэффициента регрессии при  -м факторе,
-м факторе,  , а именно:
, а именно:
 .
.
Оценка значимости коэффициентов чистой регрессии по  -критерию Стьюдента может быть проведена и без расчета частных
-критерию Стьюдента может быть проведена и без расчета частных  -критериев.
-критериев.
В этом случае, как и в парной регрессии, для каждого фактора используется формула:
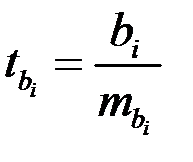 ,
,
где
 – коэффициент чистой регрессии при факторе
– коэффициент чистой регрессии при факторе  ,
,
 – средняя квадратическая (стандартная) ошибка коэффициента регрессии
– средняя квадратическая (стандартная) ошибка коэффициента регрессии  .
.
Для уравнения множественной регрессии
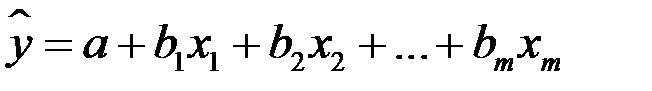
средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
 ,
,
где
 – среднее квадратическое отклонение для признака
– среднее квадратическое отклонение для признака 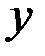 ,
,
 – среднее квадратическое отклонение для признака
– среднее квадратическое отклонение для признака  ,
,
 – коэффициент детерминации для уравнения множественной регрессии,
– коэффициент детерминации для уравнения множественной регрессии,
 – коэффициент детерминации для зависимости фактора
– коэффициент детерминации для зависимости фактора  со всеми другими факторами уравнения множественной регрессии;
со всеми другими факторами уравнения множественной регрессии;
 – число степеней свободы для остаточной суммы квадратов отклонений.
– число степеней свободы для остаточной суммы квадратов отклонений.
Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации  .
.
Так, для уравнения

оценка значимости коэффициентов регрессии  ,
,  ,
,  предполагает расчет трех межфакторных коэффициентов детерминации:
предполагает расчет трех межфакторных коэффициентов детерминации:  ,
,  ,
,  .
.
Взаимосвязь показателей частного коэффициента корреляции, частного  -критерия и
-критерия и  -критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов.
-критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов.
Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам  и
и  .
.
Частный  -критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.
-критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом.
Пример. Оценим качество уравнения, полученного ранее.
Сначала найдем значения парных коэффициентов корреляции:
 ;
;
 ;
;
 .
.
Значения парных коэффициентов корреляции указывают на достаточно тесную связь сменной добычи угля на одного рабочего  с мощностью пласта
с мощностью пласта  и на умеренную связь с уровнем механизации работ
и на умеренную связь с уровнем механизации работ 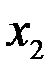 .
.
В то же время межфакторная связь 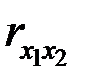 не очень сильная (
не очень сильная ( ), что говорит о том, что оба фактора являются информативными, т.е. и
), что говорит о том, что оба фактора являются информативными, т.е. и  , и
, и 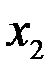 необходимо включить в модель.
необходимо включить в модель.
Теперь рассчитаем совокупный коэффициент корреляции  .
.
Для этого сначала найдем определитель матрицы парных коэффициентов корреляции:
 ,
,
и определитель матрицы межфакторной корреляции:
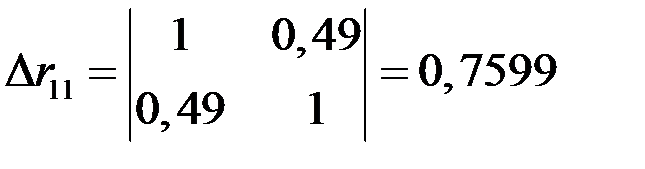 .
.
Тогда коэффициент множественной корреляции по формуле:
 .
.
Т.е. можно сказать, что 81,7% (коэффициент детерминации  ) вариации результата объясняется вариацией представленных в уравнении признаков, что указывает на весьма тесную связь признаков с результатом.
) вариации результата объясняется вариацией представленных в уравнении признаков, что указывает на весьма тесную связь признаков с результатом.
Примерно тот же результат (различия связаны с ошибками округлений) для коэффициента множественной регрессии получим, если воспользуемся формулами:
 ;
;
 .
.
Скорректированный коэффициент множественной детерминации

указывает на умеренную связь между результатом и признаками.
Это связано с малым количеством наблюдений.
Теперь найдем частные коэффициенты корреляции по формулам:
 ;
;
 .
.
 ;
;
 .
.
Т.е. можно сделать вывод, что фактор  оказывает более сильное влияние на результат, чем признак
оказывает более сильное влияние на результат, чем признак 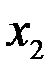 .
.
Оценим надежность уравнения регрессии в целом и показателя связи с помощью  -критерия Фишера. Фактическое значение
-критерия Фишера. Фактическое значение  -критерия
-критерия
 .
.
Табличное значение  -критерия при пятипроцентном уровне значимости (
-критерия при пятипроцентном уровне значимости ( ,
, 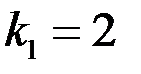 ,
,  ):
):
 .
.
Так как
 ,
,
то уравнение признается статистически значимым.
Оценим целесообразность включения фактора  после фактора
после фактора  и
и  после
после  с помощью частного
с помощью частного  -критерия Фишера:
-критерия Фишера:
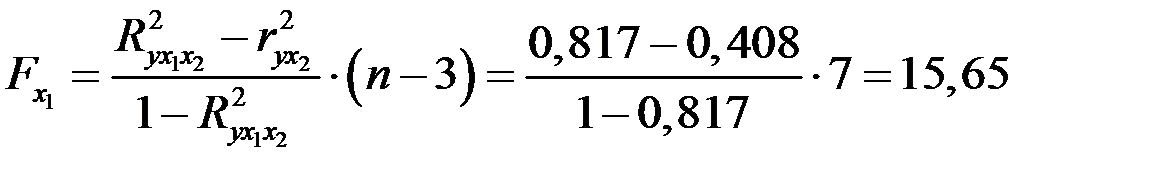 ;
;
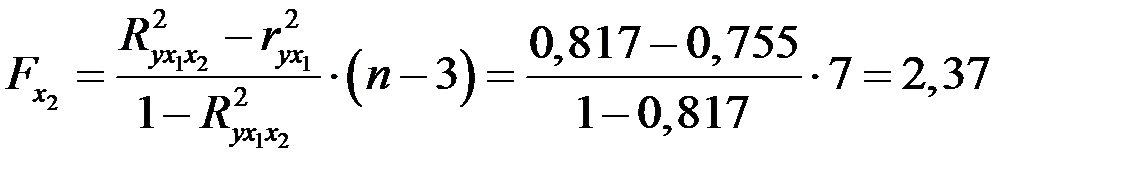 .
.
Табличное значение частного  -критерия при пятипроцентном уровне значимости (
-критерия при пятипроцентном уровне значимости ( ,
,  ,
,  ):
):
 .
.
Так как
 ,
,
а
 ,
,
то включение фактора  в модель статистически оправдано и коэффициент чистой регрессии
в модель статистически оправдано и коэффициент чистой регрессии  статистически значим, а дополнительное включение фактора
статистически значим, а дополнительное включение фактора  , после того, как уже введен фактор
, после того, как уже введен фактор  , нецелесообразно.
, нецелесообразно.
Уравнение регрессии, включающее только один значимый аргумент  :
:
 .
.
|
|
|


