 |
Множества и операции над ними.
|
|
|
|
Множества – совокупность некоторых объектов, объединенных по какому-то признаку.
Объекты из которых состоит множество, называются элементами. Множества принято обозначать заглавными латинскими буквами А,B,C…,а их элементы - малыми буквами.
Множество, не содержащее ни одного элемента, называется пустым множеством.
Элементы множества записывают в фигурных скобках, внутри которых они перечислены.
Множество А называется подмножеством В, если каждый элемент множества А является элементом множества В.
Множества А и В равны или совпадают, если они состоят из одних и тех же элемнтов.
Объединение – множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.
Пересечение – множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В.
Множества, элементами которых являются числа, называются числовыми.

Множество К содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью.
Предел последовательности.
Число а называется пределом последовательности, если для любого положительного числа Е найдется такое натуральное число N, что при всех n>N выполняется равенство:
 . В этом случае пишут
. В этом случае пишут  и говорят, что последовательность {xn}имеет предел, равный числу а. говорят,что последовательность сходится к а.
и говорят, что последовательность {xn}имеет предел, равный числу а. говорят,что последовательность сходится к а.
Коротко определение предела:  .
.
Сходящаяся последовательность имеет только один предел. Последовательность, неимеющая предела, называется расходящейся.
Если  =0 => последовательность бесконечно малая.
=0 => последовательность бесконечно малая.
Если  =
=  => бесконечно большая.
=> бесконечно большая.
 =>
=> 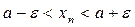 .
.
 - окрестности точки а.
- окрестности точки а.
|
|
|
Теоремы о пределах последовательности.
Теорема 1: (необходимый признак числовой последовательности):
если последовательность сходится, то она ограничена., если последовательность неограниченна, то она расходится.
Теорема Вейерштрасса: сформируем достаточный признак числовой последовательности: всякая ограниченная монотонная последовательность имеет предел.
Теорема: если две последовательности {xn}и {yn} сходятся, т.е. имеют конечные пределы, то сходятся также сумма, разность, произведение, частное этих последовательностей, т.е.:
 =>
=>  и тд.
и тд.
Теорема: если  и начиная с некоторого номера выполняется неравенство xn
и начиная с некоторого номера выполняется неравенство xn  yn, то а
yn, то а  b.
b.
Доказательство:
допустим, что а>b. Из равенств  следует, что для любого
следует, что для любого 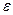 >0 найдется такое натуральное число N(
>0 найдется такое натуральное число N(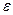 ), что при всех n>N(
), что при всех n>N(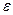 ) будут выполняться неравенства
) будут выполняться неравенства  и
и 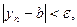 т.е.
т.е.
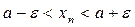 и
и  . Возьмем
. Возьмем  . Тогда:
. Тогда:  отсюда следует, что xn>yn, это противоречит условию xn
отсюда следует, что xn>yn, это противоречит условию xn  yn следовательно, а
yn следовательно, а  b.
b.
Предел функции.
Сформулируем два, эквивалентных между собой, определения предела функции в точке:
Определение (по Коши): число А называется пределом функции в точке х0, если для любого положительного 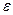 найдется такое положительное число
найдется такое положительное число  , что для всех х
, что для всех х  х0, удовлетворяющих неравенству
х0, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 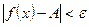 .
.
Коротко это определение:
 .
.
Определение (по Гейне):
Число А называется пределом функции  в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции
в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции  ,
, 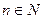 , сходится к числу А.
, сходится к числу А.
Односторонние пределы:
число А называется пределом функции  слева в точке x0, если для любого число
слева в точке x0, если для любого число  >0 существует число
>0 существует число  =
=  (
(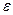 )>0 такое, что при
)>0 такое, что при  выполняется неравенство
выполняется неравенство 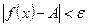 .
.
Предел слева записывают так: 
Аналогично определяется предел функции справа:
 .
.
Пределы функции слева и справа называются односторонними пределами.
Предел функции при 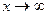 :
:
|
|
|
Число А называется пределом функции при 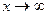 , если для любого положительного числа
, если для любого положительного числа 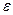 существует такое число М=М(
существует такое число М=М(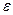 ) >0, что при всех х, удовлетворяющих неравенству
) >0, что при всех х, удовлетворяющих неравенству  выполняется неравенство
выполняется неравенство 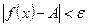 . Коротко:
. Коротко:

|
|
|


