 |
Производная функции, заданной параметрически.
|
|
|
|
Пусть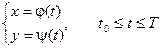 
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].
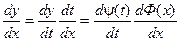
т.к. Ф(х) – обратная функция, то 
Окончательно получаем: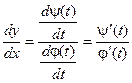 
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
50. Теоремы о среднем. Правило Лопиталя-Бернулли. Формулы Тейлора и МакЛорена.
Теорема Роля: Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и на концах отрезка принимает одинаковые значения f(a)=f(b), то найдется хотя бы одна точка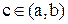 
, в которой производная 
обращается в ноль, т.е. 
.
Теорема Коши: Если функции f(x) и 
непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем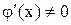 
для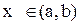 
, то найдется хотя бы одна точка 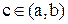, такая, что выполняется равенство 
.
Теорема Лагранжа: Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), то найдется хотя бы одна точка 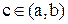такая, что выполняется равенство 
. Это так же является формулой о конечном приращении: приращение дифференцируемой функции на отрезке [a,b] равно приращению аргумента, умноженному на значение производной функции в некоторой точке этого отрезка. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое. Правило Лопиталя (по раскрытию неопределенностей вида 0/0): Пусть функции f(x) и непрерывны и дифференцируемы в окрестности точки 
и обращаются в ноль в этой точке: f()= 
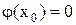. Пусть 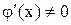в окрестности точки . Если существует предел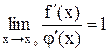 
, то 
.
Правило Лопиталя (по раскрытию неопределенностей вида 
): Пусть функции f(x) и непрерывны и дифференцируемы в окрестности точки (кроме, может быть, точки ), в этой окрестности 
. Если существует предел 
.
|
|
|
51.Монотонность функции. Экстремум. Необходимые и достаточные условия.
Теорема(необходимые условия). Если дифференцируемая на интервале (a,b) функция f(x) возрастает (убывает), то 
для любых 
. Док-во. Пусть функция f(x) возрастает на интервале (a,b). Возьмем произвольные точки х и х +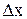 
на интервале (a,b) и рассмотрим отношение 
. Функция f(x) возрастает, поэтому если 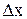>0, то x+ 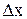>x и f(x+ 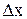)>f(x); если 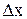<0, то x+ 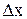>x и f(x+ 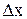)<f(x). В обоих случаях >0, так как числитель и знаменатель дроби имеют одинаковые знаки. По условию теоремы функция f(x) имеет производную в точке x и является пределом рассматриваемого отношения. Следовательно,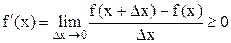 
. Аналогично рассматриваем тот случай, когда функция f(x) убывает на интервале (a,b). Данная теорема означает, что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси Ox или в некоторых точках параллельны оси Ox.
Теорема(достаточные условия). Если функция f(x) дифференцируема на интервале (a,b) и 
для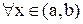 
, то эта функция возрастает (убывает) на интервале (a,b). Док-во. Пусть 
. Возьмем точки 
и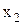 
из интервала (a,b), причем > 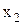. Применим к отрезку [ , 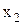] теорему Лагранжа: f(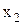) - f()= 
, где 
. По условию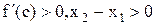 
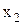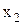. Следовательно, f() - f()>0 или f()>f(), т.е. функция f(x) на интервале (a,b) возрастает. Возрастающая или убывающая функция называется монотонной. Теорема (необходимое условие экстремума). Если дифференцируемая функция y=f(x) имеет экстремум в точке , то ее производная в этой точке равна нулю: 
. Док-во: Пусть, для определенности, -точка максимума. Значит, в окрестности точки выполняется неравенство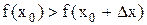 
. Но тогда 
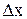, если >0, и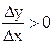 
, если 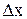<0. По условию теоремы производная 
существует. Переходя к пределу, при 
, получим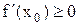 
, если 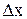<0 и 
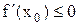, если 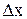>0. Поэтому: . Теорема (достаточное условие экстремума): Если непрерывная функция f(x) дифференцируема в некоторой 
-окрестности и критической точки и при переходе через нее 9слева направо) производная меняет знак с плюса на минус, то есть точка максимума; с минуса на плюс, то -точка минимума. Док-во: рассмотрим -окрестность точки . Пусть выполняются условия: 
и 
. Тогда функция f(x) возрастает на интервале 
, а на интервале 
она убывает. Отсюда следует, что значение f(x) в точке является наибольшим на интервале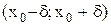 
, т.е. f(x)<f() для всех 
. Это и означает, что - точка максимума функции.
|
|
|
52. Выпуклость, вогнутость, точки перегиба. Необходимые и достаточные условия. Асимптоты. Общая схема исследования функции.
- График функции y=f(x) назыв. выпуклым (вверх) на отрезке [a,b], если он расположен ниже касательной. Для дифференцируемой на [a,b] функции график расположен ниже любой касательной; для недифференцируемой функции график расположен выше хорды((a, f(a) и (b, f(b))).
- График функции назыв. вогнутым (выпуклым вниз) на [a,b], если он расположен выше касательной (ниже хорды). Если в левой U() график функции выпуклый в одну сторону, а в правой окрестности в другую сторону, то -точка перегиба.
- Если функция y=f(x) дважды дифференцируема на [a,b] и для любых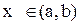 
, то график является выпуклым вниз(вогнутым). Если 
, то график является выпуклым. Достаточное условие точки перегиба: Пусть f - дважды дифференцируемая функция в окрестности и 
или 
не существует. Если при этом для любых 
, а для любых 
, то - точка перегиба.
Асимптоты. При исследовании поведения графика функции либо в бесконечности, либо вблизи точек разрыва второго рода часто оказывается, что график приближается к некоторой прямой линии. Другими словами, расстояние между точками графика функции и точками прямой линии, измеренные по вертикали и горизонтали, стремится к нулю. Такие прямые линии – асимптоты графика функции. Бывают вертикальные (точки разрыва 2ого рода), либо наклонные (поведение функции в бесконечности). Горизонтальная асимптота – частный случай наклонной. Непрерывные функции не имеют вертикальных асимптот. Для того, чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы 
.
|
|
|
Общая схема исследования функции. 1. Находим область определения D(x). 2. Находим точки разрыва второго род, обозначаем вертикальные асимптоты. 3. Исследуем функцию на четность/нечетность, периодичность. 4. Находим точки пересечения с Ox и Oy. С Ox: x=o, y-?. C Oy: y=0, x-? 5. Находим наклонные асимптоты, если они есть. 6. Исследуем функцию на наличие критических точек. Решаем уравнение 
. 7. Определяем промежутки монотонности. 8. Находим вторую производную и точки, для которых она равна 0 или не существует. 9. Находим промежутки знакопостоянства второй производной. 10. Составляем таблицу. 11. на основе таблицы определяем точки локального экстремума и точки перегиба.
53. Вектор-функция скалярного аргумента. Годограф. Производная. Касательная прямая и нормальная плоскость.
Векторная функция скалярного аргумента.
 |
A(x, y, z)
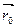
Пусть некоторая кривая в пространстве задана параметрически: x = j(t); y = y(t); z = f(t); Радиус- вектор произвольной точки кривой: 
.
Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора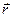 
. Запишем соотношения для некоторой точкиt0: 
Тогда вектор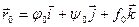 
- предел функции 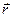(t). 
. Очевидно, что 
, тогда 
. Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
; 
;
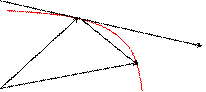
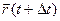
или, если существуют производные j¢(t), y¢(t), f¢(t), то 
.
Это выражение – вектор производная вектора .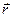 
; 
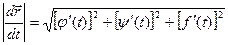. Если имеется уравнение кривой: x = j(t); y = y(t); z = f(t); то в произвольной точке кривой А(xА, yА, zА) с радиус- вектором
можно провести прямую с уравнением 
. Т.к. производная - вектор, направленный по касательной к кривой, то 
. Уравнение нормальной плоскости к кривой будет иметь вид: 
.
Определение: Линия, которую опишет в пространстве переменный радиус – вектор 
при изменении параметра S, называется годографом этого вектора. 
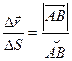, тогда 
- вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к. 
, то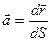 
- единичный вектор, направленный по касательной. Если принять 
, то 
.
|
|
|
Причем 
. Рассмотрим вторую производную 
Определение: Прямая, имеющая направление вектора 
называется главной нормалью к кривой. Ее единичный вектор обозначается 
. 
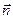, где К – кривизна кривой.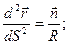 
54. Кривизна и кручение. Кривизна пространственной кривой.
z
B
A(x, y, z) 
0 y
x
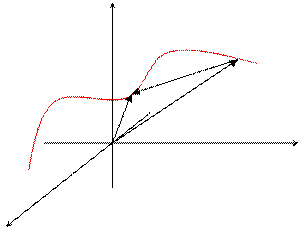
Для произвольной точки А, находящейся на пространственной кривой, координаты могут быть определены как функции некоторой длины дуги S.
x = j(S); y = y(S); z = f(S);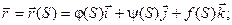 
Приведенное выше уравнение называют векторным уравнением линии в пространстве.
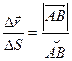Определение: Линия, которую опишет в пространстве переменный радиус – вектор при изменении параметра S, называется годографом этого вектора. , тогда - вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к. , то 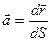- единичный вектор, направленный по касательной. Если принять , то . Причем . Рассмотрим вторую производную Определение: Прямая, имеющая направление вектора называется главной нормалью к кривой. Ее единичный вектор обозначается .
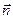, где К – кривизна кривой. 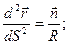Кривизна пространственной кривой может быть найдена по формуле: 
Возможна и другая запись формулы для кривизны пространственной кривой (она получается из приведенной выше формулы):
Определение: Вектор 
называется вектором кривизны. Величина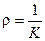 
называется радиусом кривизны.
Величина 
называется кручением кривой.
55. Сопровождающий трёхгранник Френе. Формулы Френе.
Под трёхгранником Френе, иначе называемым естественным, сопровождающим или сопутствующим трёхгранником или репером, понимают тройку векторов 
сопоставленную каждой точке гладкой кривой, где 
— единичный касательный вектор, 
— единичный вектор главной нормали,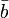 
— единичный вектор бинормали к кривой в данной точке. Если s — натуральный параметр вдоль кривой, то векторы вязаны соотношениями:
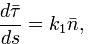
называемыми формулами Френе и задающими натуральное уравнение кривой.
|
|
|
