 |
10 Виды интервалов группировок и их определение.
|
|
|
|
10 Виды интервалов группировок и их определение.
В типол-ой групп-ке по атрибутивному пок-лю число групп соотв-ет кол-ву видов признака. Если групп-ный признак числовой, то, как правило, он принимает 1-4 значения. В структурной или вариационной группировке весь объем явления принимается за 100% или 1, находятся его доли, которые и определяют число групп.
В аналитической группировке по количественному признаку число групп и величины интервалов определся:
1) эксперим–иссл.
2) ф-ла Стерджесса, где N – число единиц. сов-ти, n = 1 +3, 322 lgN: 
3) с произв-ми интервалами, если она мала по объему
Интервалы групп-к бывают:
Равные и неравные; открытые и закрытые.
11 Равночастотные групп-ки и их исп-е.
Равночастотная групп-ка – это когда в каждой группе одинак. или почти одинак. кол-во объектов.
12 Система группировок. Перегруппировка.
Система группировок – это ряд взаимосвязанных статистических группировок по наиболее характерным, существенным признакам, всесторонне отражающим важнейшие стороны изучаемых процессов и явлений.
При сравн-и разл-х сов-тей или одной и той же сов-ти, но за разные периоды времени может возникнуть проблема: сравн-е разл-х групп-к с разными интервалами. Следует привести информацию к сопоставимому виду.
Пол-е новых групп на осн-и имеющихся возможно двумя способами:
1) перегруппировка по величине интервалов первичной группировки,
2) перегруппировка по удельному весу отдельных групп в общем их итоге.
13 Использование дисперсионного анализа в группировках.
Предполагаемое утверждение называть рабочей гипотезой. " ноль-гипотеза" -отсутствие достоверных связей между анализ-ми показателями.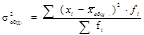 
|
|
|
где Хi – значение пок-ля у кажд. ед.,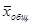 
– ср. значение пок-ля по всей сов-ти, f– частота значений пок-ля.
где 
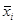- среднее значение показателя каждой группе.
Эмпирический коэф-т корреляции η отражает силу связи между результативным и факторным показателем. Если 0< η ≤ 0, 3 – связь слабая0, 3 ‹ η ≤ 0, 7 – связь средняя0, 7 ‹ η ≤ 1 – связь тесная. Эмпирический коэффициент корреляции вычисляют по формуле:
Эмпирический коэффициент детерминации η 2 показывает, какая часть вариации результативного показателя зависит от вариации факторного признака.
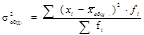
На базе полученных дисперсий вычисляют значение F–критерия (критерия Фишера) по одной из формул:
" ν " - " число степеней свободы":
ν м. г. = m – 1, где m – число групп
ν ост. = n – m, где n – объём изуч. сов-ти
Отношение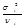 
называется средним квадратом и часто обозн-ся как 
, тогда 
Расчетное значение F-критерия необходимо сравнить с табличным значением критерия Фишера.
Fрасчетное > Fтабл. -опровергается " ноль-гипотеза; Fтабл. ≥ F расч. -подтверждается " ноль-гипотеза"
15 Понятие средней величины.
Средней величиной наз-ся обобщ-й пок-ль, характер-щий типичный уровень варьирующего признака в качественно-однородной сово-ти.
Средние, характ-ие сис-му, сов-ть в целом, наз-ся системными или общими средними.
Средние, характ-ие подсистемы, типические группы или подгруппы, наз-ся групповыми.
Формы средних и их применение.
Введем обозначения: Хi – варианта; fi – частота (повторяемость) варианты; Wi – объем явления (Хi * fi = Wi).
|
|
|
1. Средняя арифметическая:
- 
простая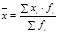 
-взвешенная
2. Средняя гармоническая:
- простая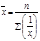 
- взвешенная
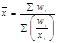
3. Средняя хронологическая:
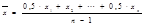
4. Средняя геометрическая:
Где 
–цепной темп роста, 
, 
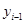–ур-ни ряда динамики.
5. Средняя квадратическая:
- Простая - взвешенная 
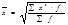
6. описательным средним
Модой(Мо) ; Медианой(Ме)
|
|
|
