 |
Парная линейная корреляционно-регрессионная модель.
|
|
|
|
Парная линейная корреляционно-регрессионная модель.
Процесс построения корреляционно-регрессионной модели сводится к осреднению значения результата и фактора. После расчета уравнения регрессии, необходимо будет проверить выполнение равенства: 
Для парной связи следует построить график (точечную диаграмму), и выявить наличие ошибок информации и (или) аномальные точки. Уравнение регрессии должно обеспечить минимум суммы квадратов отклонений эмпирических значений результативного показателя от теоретических значений, полученных по модели: ỹ х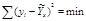 
Это достигается при использовании метода наименьших квадратов, разработанного К. Ф. Гауссом
Парный коэффициент регрессии показывает, на сколько единиц своего измерения в среднем изменится результат (У), если факторный показатель (Х) изменится в среднем на единицу своего измерения.
20 Показатели тесноты связей линейной корреляционно-регрессионной модели:
1. ) Парный коэффициент корреляции: 
или 
Величина 
- 
наз-ся ковариацией и обозн-ся
- 
= COVyx (это пок-ль величины совм-й вариации Х и Y).
0< r< 1 - прямая; –1< r< 0 -обратная.
|r|< =0, 3- слабая; 0, 3< |r|< 0, 7-средняя; |r|> =0, 7- сильная (или тесная).
2. ) Парный коэффициент детерминации 
Он показывает, на сколько процентов вариация результата зависит от вариации фактора.
3. ) Коэффициент эластичности (Э).
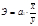
Коэф-т эластичности показывает, на сколько процентов изменится в среднем результат (У) при изменении фактора (Х) на 1% своего среднего значения.
|
|
|
Анализ достоверности парной линейной коррел-регрес. модели.
Для линейной связи обычно используют t-критерий (критерий Стьюдента). Определяют t расчетные для параметров уравнения и силы связи факторов a0, a1 и r. Сравнивают полученные значения с t табличными. Если расчетные t больше t табличных, то ноль-гипотеза о недостоверности уравнения отвергается. По формулам: 
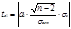
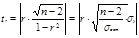
-- число степеней свободы.
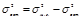
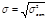
t табличное находим по значению 
преимущественно при вероятности p=0. 90; p=0. 95; p=0. 99.
22 Показатели тесноты связи факторов при множественном корреляционно-регрессионном анализе.
Оценка тесноты связи Y со всеми Xi произв-ся с пом-ю сов-го коэффициента детерминации: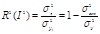 
где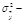 
факторная дисперсия; 
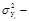общая дисперсия; 
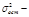остат-я дисперсия и сов-го коэффициента корреляции: 
Сов-й коэф-т детерминации R2 может быть выражен в %. Он пок-ет, какая часть вариации результативного пок-ля объясняется вариацией факторов, вкл-х в модель. Сов-й коэффициент корреляции всегда 0< R< 1. Он отражает только тесноту связи и не может отражать направление связи. Чем ближе R к 1, тем влияние факторов на результат сильнее, чем ближе к 0 – тем влияние слабее.
След. группа пок-лей, отражающих связи факторов, вкл-х в модель – это коэф-ты эластичности и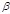 
– коэф-ты. Коэф-т эластичности пок-ет, на сколько % в среднем изменится результат (У) при изменении фактора Хi в среднем на 1 % при условии неизменности остальных факторов, входящих в модель.
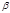– коэф-т пок-ет, на сколько среднеквадратических отклонений изменяется результат (У) при изменении фактора Хi на одно свое среднеквадратическое отклонение, при неизменности остальных факторов входящих в уравнение. Для парной линейной регрессии выполняется равенство 
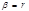. Поэтому в парном корреляционно-регрессионном анализе 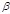— коэффициент не рассматривался.
|
|
|
|
|
|
