 |
26 Тренд. Прогнозы по тренду. 27 Сезонные колебания в рядах динамики. 28 Корреляция рядов динамики. Регрессия рядов динамики.
|
|
|
|
26 Тренд. Прогнозы по тренду.
Под трендом понимают уравнение линии во времени, вдоль которой расположена ломаная ряда динамики.
Этапы построения тренда:
1. Выявляют этапы развития явления (спады, подъемы, однородные участки и т. д. ).
2. Анализируют показатели ряда динамики на этих этапах и выбирают вид уравнения (вид тренда).
3. Вычисляют параметры тренда, используя метод наименьших квадратов.
4. Оценивают адекватность уравнения, развитию анализируемого показателя, оценивая колеблемость фактических уровней ряда вокруг теоретических, т. е. вычисленных по тренду.
Прогноз по тренду. Используя уравнение можно построить точечный прогноз на последующие периоды времени, подставляя в уравнение тренда номера t, следующие за последним фактическим номером, используемым при построении тренда.
27 Сезонные колебания в рядах динамики
Если ряд динамики насчитывает достаточное количество уровней, , то можно обнаружить колебания, которые повторяются, т. е. наличие регулярных спадов и подъёмов, наз-ся циклическими. Внутри годичные колебания, имеющие регулярный характер, т. е. повторяющиеся из года в год, называются сезонными. Чаще всего степень сезонных колебаний определяют по величине индекса сезонности. 
Оценка индекса сезонности осущ-ся по среднелинейному или среднеквадратическому отклонению для каждого года. Среднее линейное отклонение:
= 
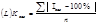Среднеквадратическое отклонение:
= 
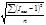где n – число сезонов.
Чем меньше значения этих показателей, тем меньше сезонная колеблемость и выше стабильность показателя.
Модели рядов с учетом тенденции и сезонности:
1) 
Ряд динамики в виде произведения уравнения тренда на средние индексы сезонных колебаний 
|
|
|
2) Уравнение в виде «гармоник ряда Фурье»: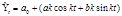 
где k определяет номер гармоник с точностью до четырёх знаков.
Под гармоникой понимают полную волну синусоиды (гармонику Фурье), где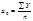 
; 
; 
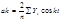28 Корреляция рядов динамики. Регрессия рядов динамики.
Перед статистическим исследование “связанных” друг с другом рядов стоит проблема:
1)оценить тесноту связи между значениями уровней различных рядов;
2) построить уравнение регрессии, связывающее результативный показатель, факторный показатель и временной параметр t.
Поскольку тех. процесс произ-ва и реализации продукции растянут во времени, то может оказаться, что каждый последующий уровень ряда зависит с определённой величиной лага l от предыдущих значений уровней ряда. Это явл-е наз. автокорреляцией. Yхt = a0 + a1 х + а2t - Это уравнение связывает только два ряда и время t.
29 Понятия интерполяции и экстраполяции в рядах динамики.
Интерполяция – это способ определения промежуточных значений динамического ряда:
а) на основе известных соседних значений (как среднее арифметическое);
б) на основе взаимосвязей с другими рядами, количественные выражения которых известны;
в) на основе средних значений показателей ряда динамики.
При проведении интерполяции предполагается, что выявленная тенденция и ее характеристики не претерпели существенных изменений в тот период времени, уровни которого отсутствуют.
Экстраполяция – это метод определения количественных характеристик для совокупностей, не подвергающихся изучению непосредственно, а на основе изучения предыдущего их развития или развития аналогичных совокупностей. Оба эти метода возможны только в условиях стабильного развития технолого-экономических показателей.
|
|
|
