 |
33 Агрегатная форма построения индексов. Классификация агрегатных индексов по составу.
|
|
|
|
33 Агрегатная форма построения индексов. Классификация агрегатных индексов по составу.
Произведения вида qp, qz, qt — называются агрегатами, а индексы, построенные на их основе — агрегатными, т. е. в агрегатном индексе и числитель и знаменатель представлены в виде суммы агрегатов. По сути Г. Пааше и Э. Ласпейрес заложили основу для построения агрегатных индексов.
Показатели z, p, t, m являются интенсивными или качественными, а показатель q – объёмным или количественным. Показатель, который в индексе меняется во времени, называется индексируемым, который не меняется — весами или соизмерителем . В зависимости от того, сколько показателей изменяется, различают индексы переменного и постоянного состава.
34 Классификация агрегатных индексов по содержанию.
Рассмотрим деление агрегатных индексов на качественные и количественные
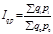Это агрегатный индекс переменного состава. Кроме того, он будет объёмным (или количественным). Для индексов постоянного состава этот вопрос решается иначе. Отнесение индекса к количественному или качественному зависит от того, какой фактор (количественный или качественный) индексируется.
Это агрегатный индекс постоянного состава. В индексе количества и структуры товара отражена динамика объёмного показателя (q), поэтому этот индекс является объёмным или количественным.
Данный агрегатный индекс цен постоянного состава отражает изменение выручки за счет изменения цен. В индексе цен определяющей является динамика качественного показателя – цены ( р ) и влияние её на товарооборот, поэтому этот индекс является качественным.
35 Классификация агрегатных индексов по базе сравнения.
|
|
|
Если в индексном анализе сравниваются показатели за два периода, то эти индексы носят название базисных. Если система индексов построена на показателях, взятых как минимум за 3 периода первые из них индексы являются базисными, а вторые – цепными. Базисные индексы выручки (стоимости товара) переменного состава: 
; 
; …; 
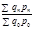Цепные индексы выручки (стоимости товара) переменного состава: 
; 
; …; 
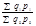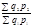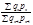
Базисные индексы физического объема постоянного состава:
; 
; ...; 
Цепные индексы физического объема постоянного состава: 
; 
…; 
.
37 Индексы ср. величин (индексы ст-ры).
1) Индекс ср. цены переменного состава. Индекс отражает изм-е ср. цены за счет динамики как кол-ва и ст-ры товара, так и за счет изм-я цен на отдельные его виды. 
Соотв-ет два абсол-ых изменения.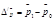 
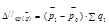
2) Индекс средней цены с пост-м составом (фиксированного состава). Этот индекс отражает изм-е ср. цены, при условии, что объем и ст-ра произв-ой или проданной прод-ции взята на ур-не отчетного периода.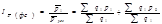 
Соответствует два абсол-х изменения
3) Индекс структурных сдвигов (постоянного (фиксированного) состава ). Отражает изм-е ср. цены прод-ции за счет изм-я долей в реал-ции разл-й прод-ции. Если ст-ра улучшается, то ср. цена реализации увеличивается.
или этот индекс можно предст-ть как частное агрегатного индекса кол-ва и ст-ры товара и индекса числ-сти прод-ции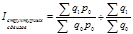 
, 
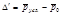
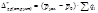
Соотн-е индексов: 
36 Геометрические индексы (идеальный индекс Фишера):
Этот индекс был получен как корень квадратный из произведения индекса Пааше на индекс Ласпейреса.
По аналогии может быть построен геометрический индекс количества товара. 
Эти индексы не имеют соответствующего абсолютного изменения.
Средний арифметический индекс физического объема продукции получим в том случае, если частотой (или повторяемостью) для индивидуального индекса iq будет служить объем товарооборота q0p0.
|
|
|
Это равенство следует и соотн-я 
При постр-и среднеарифметического индекса цен необходимо определиться с весами (в нашей формуле это веса Г. Пааше). Тогда средний арифметический индекс цен будет равен агрегатному индексу цен Пааше. 
Данное равенство индексов обеспечивается за счет соотношения:
Средний гармонический индекс.
Средний гармонический индекс цен с весами Г. Пааше будет иметь вид: 
Рав-во обесп-ся соотн-ем:
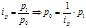
Средний гармонический индекс количества и структуры товара будет построен следующим образом.
Данное равенство обеспечивается соотношением 
|
|
|
