 |
Задача 1. «Сложное движение точки»
|
|
|
|
Кафедра инженерной графики и механики
Д.В. Мотин
Н.М. Иванушкина
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
Варианты заданий к расчётно-графическим работам и методические указания к их выполнению для бакалавров направлений 110800 «Агроинженерия» и 280700 «Техносферная безопасность»
Орел – 2012
УДК 531.3(07)
Автор: ст. преподаватель Д.В. Мотин (ОГАУ),
ст. преподаватель Н.М. Иванушкина (ОГАУ)
Рецензент: доцент Орел ГТУ Прокопов Е.Е.
Методические указания содержат варианты заданий к расчётно-графическим работам по теоретической механике и рекомендации по их выполнению и оформлению, приведены примеры решения задач. Указания рассмотрены и одобрены кафедрой «Инженерная графика и механика».
СОДЕРЖАНИЕ
| Введение………………………………………………………………………… | |
| 1.Порядок выбора вариантов и оформления расчётно-графических работ…. | |
| 2. Задача 1. «Сложное движение точки»……………………………………….. | |
| 3. Задача 2. «Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил»………... | |
| 4. Задача 3. «Применение теоремы об изменении кинетического момента к определению угловой скорости твердого тела»……………………………….. | |
| 5. Задача 4. «Применение теоремы об изменении кинетической энергии к изучению движения механической системы»……………………………….……… | |
| 6. Задача 5. «Принцип Даламбера. Решение динамической задачи методом кинетостатики»…………………………………………………………………… | |
| Список литературы………………………………………………………………. | |
| Приложение………………………………………………………………………. |
Введение
|
|
|
Теоретическая механика наряду с математикой и физикой относится к числу фундаментальных дисциплин инженерного образования. Инженерная грамотность студентов во многом определяется знаниями, полученными на первых трех курсах при изучении именно этих дисциплин. Изучение теоретической механики является важнейшим фактором углубления специальной подготовки инженера, служит базой для освоения таких важнейших для него дисциплин как сопротивление материалов, теория механизмов и машин, детали машин и т.п. Теоретическую механику невозможно изучать без решения задач.
Теоретическая механика, являясь научной основой важнейших областей техники, продолжает развиваться. Это стимулируется появлением новых технологий и производств, автоматизацией производственных процессов, созданием новых высокоскоростных машин и механизмов, освоением космического пространства. Прогресс современного производства невозможен без широкого взаимодействия науки и техники. Для решения этих возрастающих по сложности задач важное значение имеют и знания в области одной из фундаментальных общенаучных дисциплин – теоретической механики.
Самостоятельное выполнение расчётно-графической работы является важным средством получения прочных знаний по предмету, позволяет глубже разобраться в теоретических вопросах.
1. Порядок выбора вариантов и оформления расчетно-графических работ
В задачах №1 и №5 дается 10 рисунков и таблица с десятью строками, содержащими дополнительные данные к задаче. Во всех задачах номер рисунка определяется последней цифрой шифра, а номер строки в таблице данных - предпоследней цифрой шифра. Например, если шифр оканчивается цифрами 08, то нужно выбрать 0 строку в таблице данных и рисунок 8.
В задачах №2, №3 и №4 номер варианта выбирается из таблицы.
| Ш И Ф Р | Номера вариантов | Ш И Ф Р | Номера вариантов | Ш И Ф Р | Номера вариантов | Ш И Ф Р | Номера вариантов | Ш И Ф Р | Номера вариантов | ||||||||||
| №задачи | №2 | №3 | №4 | №2 | №3 | №4 | №2 | №3 | №4 | №2 | №3 | №4 | №2 | №3 | №4 | ||||
|
|
|

Расчётно-графическая работа выполняется на листах писчей бумаги формата А4 с одной стороны. Первая страница - титульный лист (образец см. в приложении 1). Вторая страница – содержание. Страницы нумеруются, начиная с третьей. Каждая задача начинается с того, что указывается её номер, записывается условие задачи. Затем выполняется чертеж (в карандаше), при этом учитываются условия решаемого варианта задачи (табличные данные).
|
|
|
Все чертежи и расчетные схемы должны быть аккуратными, хорошо читаемыми, с нанесенными на них координатными осями, силами, линейными размерами, углами и т.п.
При решении задач необходимо давать краткие пояснения (какие формулы или теоремы применяются, откуда получены те или иные величины и т.п.), подробно излагать последовательность вычислений, по окончании вычислений проверить правильность и дать анализ полученного решения.
Задача 1. «Сложное движение точки»
Прямоугольная пластина (рис. 0 – 5) или круглая пластина радиуса R=60см (рис. 6 – 9) вращается вокруг неподвижной оси с постоянной угловой скоростью ω, заданной в таблице (при знаке минуc направление вращения противоположно направлению показанному на рисунке). Ось вращения на рис. 0, 1, 2, 3, 6, 7 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 4, 5, 8, 9 ось вращения О1О2 - вертикальная (лежит в плоскости пластины).
По пластине, вдоль прямой BD(рис. 0 – 5) или по окружности радиуса R (т.е. по ободу пластины) (рис. 6 – 9), движется точка М. Закон её относительного движения, выражаемый уравнением S=AM=f (t) (S в сантиметрах, t в секундах), задан в таблице; там же даны размеры а и h (для рис. с 0 по 5 - в столбцах 3 и 4; для рис. с 6 по 9 – в столбцах 5 и 6). Положительное направление отсчёта координаты S =AM от точки А к точке D (на всех рисунках точка Mпоказана в положении, при котором S=AMположительно).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1с.
| № условия | ω рад/с | Puc. 0 – 5 | Puc. 6 – 9 | ||
| a, см | S=AM=f (t) | h | 
| ||
| – 2 | 60(t4 – 2t2) + 56 | R | 
| ||
| 60(t3 – 2t2) | R | 
| |||
| 80(2t2 – t3) – 48 | R | 
| |||
| – 4 | 40(t2 – 3t) + 32 |  R R
| 
| ||
| 50(t3 – t) – 30 | R | 
| |||
| 50(3t – t2) – 64 | R | 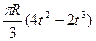
| |||
| 40(t – 2t3) – 40 |  R R
| 
| |||
| – 5 | 80(t2 – t) + 40 | R | 
| ||
| 60(t – t3) + 24 | R | 
| |||
| – 5 | 40(3t2 – t4) – 32 |  R R
| 
|
|
|
|


Пример решения Задачи 1
Условие задачи:
Прямоугольная пластина вращается вокруг неподвижной оси перпендикулярной плоскости чертежа и проходящей через точку О с постоянной угловой скоростью  ,
,
По поверхности пластины, по прямой BD, движется точка M. Закон её движения задаётся функцией  . Начало отсчёта координаты S – точка А, положительное направление отсчета координаты
. Начало отсчёта координаты S – точка А, положительное направление отсчета координаты  - от точки A к точке D.
- от точки A к точке D.
Требуется найти абсолютную скорость и абсолютное ускорение точки M в момент времени t = 1 с

Рис. 1.1
Решение задачи
Движение точки M - сложное. Её абсолютное движение складывается из движения по стороне ВД пластины – относительное движение и движения точки М вместе с вращающейся пластиной – переносное движение.
Абсолютная скорость точки М
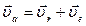 ,
,
где  – относительная скорость
– относительная скорость  ;
;
 – переносная скорость
– переносная скорость  ;
;
Абсолютное ускорение точки


 ,
,
где  – относительное ускорение;
– относительное ускорение;
 – переносное ускорение,
– переносное ускорение,
 – ускорение Кориолиса,
– ускорение Кориолиса,
 – - относительное касательное ускорение,
– - относительное касательное ускорение,
 – относительное нормальное ускорение.
– относительное нормальное ускорение.
 – переносное касательное ускорение,
– переносное касательное ускорение,
 – переносное нормальное ускорение.
– переносное нормальное ускорение.
Рассмотрим относительное движение точки.
Скорость относительного движения


Относительное касательное ускорение
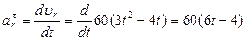

Относительное нормальное ускорение

 , так как точка M в относительном движении перемещается по прямой BD, то
, так как точка M в относительном движении перемещается по прямой BD, то  , тогда
, тогда 
Модуль относительного ускорения 
Для момента времени t=1 c:
AM= 
 (знак минус показывает, что движение направлено от точки А к точке В);
(знак минус показывает, что движение направлено от точки А к точке В);


(вектор  направлен к B);
направлен к B);

 (вектор направлен к точке D);
(вектор направлен к точке D);

 (
( )
)
Строим чертеж с нанесением положения точки, векторов относительных скорости и ускорения в момент t = 1 c

Рис.1.2
Переносное движение
Угловая скорость переносного движения 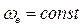 , следовательно, угловое переносное ускорение
, следовательно, угловое переносное ускорение

Переносная скорость точки M

В момент времени t=1c

Переносное касательное ускорение

Переносное нормальное ускорение

Кориолисово ускорение

(вектор  направлен вдоль оси вращения)
направлен вдоль оси вращения)
Вектор  перпендикулярен плоскости, в которой расположены векторы
перпендикулярен плоскости, в которой расположены векторы  и
и 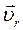 и направлен в ту сторону, чтобы с его конца поворот вектора
и направлен в ту сторону, чтобы с его конца поворот вектора  (первый сомножитель) до совмещения его с вектором
(первый сомножитель) до совмещения его с вектором  (второй сомножитель) по кратчайшему пути был виден происходящим против хода стрелки часов.
(второй сомножитель) по кратчайшему пути был виден происходящим против хода стрелки часов.
Абсолютное движение
Абсолютная скорость точки М

Сумму векторов найдем через проекции на оси координат X и У

 (
( )
)


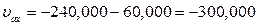






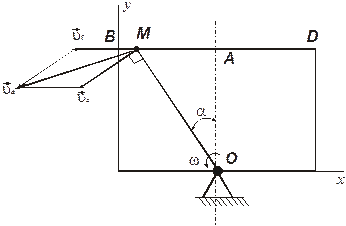
Рис.1.3
Абсолютное ускорение
Абсолютное ускорение точки М для нашего случая
|
|
|

Сумму векторов найдем через их проекции на оси координат X и У

для момента времени t=1c



 ( см/с2)
( см/с2)

Рис.1.4
|
|
|


