Статическое описание квантовой системы. Распределение Бозе — Эйнштейна и Ферми — Дирака

Квантовая статистика — раздал статистической физики, исследующий системы, кото­рые состоят из огромного числа частиц, подчиняющихся законам квантовой механики.

В отличие от исходных положений классической статистической физики, в которой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основывается на принципе неразличимости тождественных ча­стиц. При этом оказывается, что коллективы частиц с целым и полуцелым спинами подчиняются разным статистикам.

Понятие о квантовой статистике Бозе — Эйнштейна и Ферми — Дирака

Одним из важнейших «объектов» изучения квантовой статистики, как и классической, является идеальный газ. Это связано с тем, что во многих случаях реальную систему можно в хорошем приближении считать идеальным газом. Состояние системы невза­имодействующих частиц задается с помощью чисел заполнения N_i — чисел, указывающих степень заполнения квантового состояния частицами системы, состоящей из многих тождест­венных частиц. Для систем частиц, образованных бозонами — частицами с нулевым или целым спином, числа заполнения могут принимать любые целые значения: 0, 1, 2,.... Для систем частиц, образованных фермионами — частицами с полуцелым спином, числа заполнения могут принимать лишь два значения: 0 для свободных состояний и 1 для занятых. Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т. е. определить средние числа заполнения á N_i ñ.

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна. Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым:

(1)

Это распределение называется распределением Бозе — Эйнштейна. Здесь á N_i ñ — сред­нее число бозонов в квантовом состоянии с энергией E_i, k — постоянная Больцмана, Т— термодинамическая температура, m —химический потенциал; m не зависит от энергии, а определяется только температурой и плотностью числа частиц

Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми — Дирака. Распределение фермионов по энергиям имеет вид

(2)

где á N_i ñ — среднее число фермионов в квантовом состоянии с энергией Е_i, m — хи­мический потенциал.

В отличие от (1) m может иметь положительное значение (это не приводит к отрицательным значениям чисел á N_i ñ). Это распределение называется распределением Ферми — Дирака.

Если 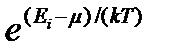>>1, то распределения Бозе — Эйнштейна (1) и Ферми — Дирака (2) переходят в классическое распределение Максвелла — Больцмана:

(3)

где

(4)

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Вырожденный электронный газ в металлах. Энергия и уровень Ферми.

 

Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Поведение как бозе-газа, так и ферми-газа отличается от классического газа, они являются вырожденными газами. Вырождение газов становится существенным при весьма низ­ких температурах и больших плотностях.

Параметром вырождения называется вели­чина А. При А <<1,т. е. при малой степени вырождения, распределения Бозе — Эйнш­тейна и Ферми — Дирака переходят в классическое распределение Макс­велла — Больцмана.

Температурой вырождения Т ₀ называется температура, ниже которой отчетливо проявляются квантовые свойства идеального газа, обусловленные тождественностью частиц, т. е. Т ₀ — температура, при которой вырождение становится существенным. Если Т >> Т ₀, то поведение системы частиц (газа) описывается классическими за­конами.

Электроны проводимости в металле можно рассматривать как идеальный газ, подчиняющийся распределению Ферми — Дирака. Если m ₀ — химический поте­нциал электронного газа при Т= 0 К, то, согласно, среднее число á N (E)ñ электронов в квантовом состоянии с энергией Е равно

(1)

Для фермионов (электроны являются фермионами) среднее число частиц в квантовом состоянии и вероятность заселенности квантового состояния совпадают, так как кван­товое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов á N (E)ñ =f(E), где f(E) — функция рас­пределения электронов по состояниям.

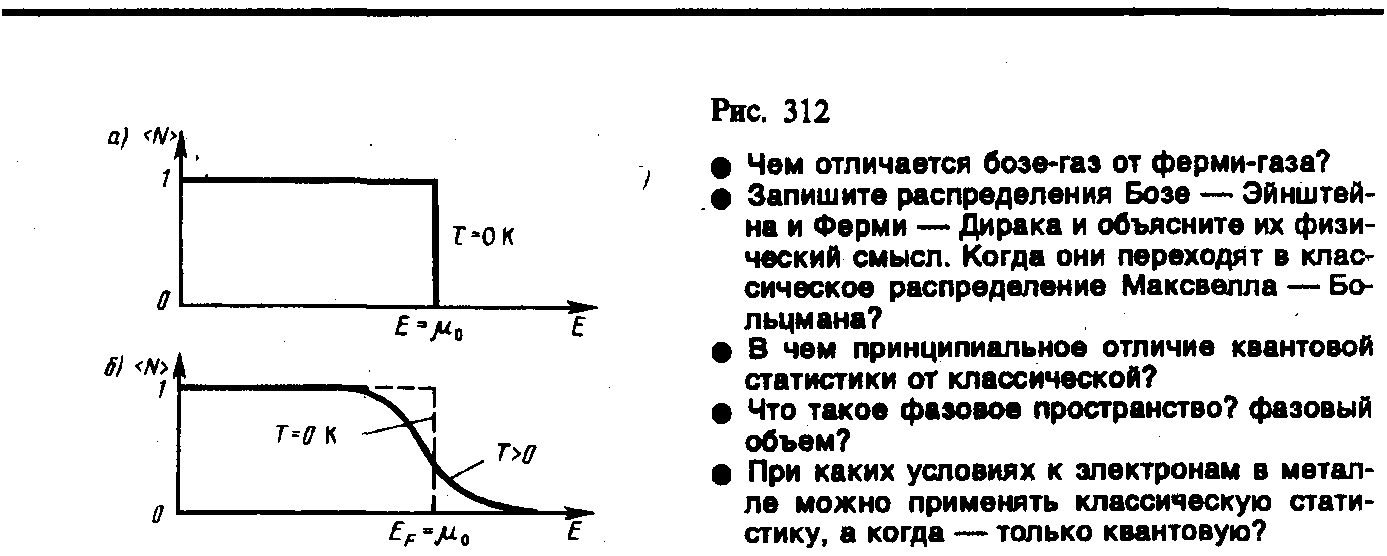
При T =0 К функция распределения á N (E)ñ = 1, если E<m ₀, и á N (E)ñ = 0, если Е>m ₀. График этой функции приведен на рис. 1, а. В области энергий от 0 до m ₀ функция á N (E)ñ равна единице. При E=m ₀ она скачкообразно изменяется до нуля. Это означает, что при Т= 0К все нижние квантовые состояния, вплоть до состояния с энергией E=m ₀, заполнены электронами, а все состояния с энергией, большей m ₀, свободны. Следовательно, m ₀ есть не что иное, как максималь­ная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта максимальная кинетическая энергия называется энергией Ферми и обозна­чается Е_F (Е_F=m ₀). Поэтому распределение Ферми — Дирака обычно записывается в виде

Рис 1

(2)

Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энергия Ферми Е_F, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода электрона из металла нужно отсчитывать не от дна «потенциальной ямы», как это делалось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых электронами энергетических уровней.

Для металлов при не слишком высоких температурах выполняется неравенство kT<<E_F. Это означает, что электронный газ в металлах практически всегда находится в состоянии сильного вырождения. Температура Т ₀ вырождения находится из условия kT ₀ =E_F. Она определяет границу, выше которой квантовые эффекты перестают быть существенными. Соответствующие расчеты показывают, что для электронов в металле T ₀»10⁴ К, т. с. для всех температур, при которых металл может существовать в твердом состоянии, электронный газ в металле вырожден.

При температурах, отличных от 0 К, функция распределения Ферми — Дирака плавно изменяется от 1 до 0 в узкой области (порядка kT) в окрестности Е_F (рис.1 б). (Здесь же для сравнения пунктиром приведена функция распределения при T =0 К.) Это объясняется тем, что при T >0 небольшое число электронов с энергией, близкой к Е_F, возбуждается вследствие теплового движения и их энергия становится больше Е_F. Вблизи границы Ферми при Е< Е_F заполнение электронами меньше еди­ницы, а при Е> Е_F — больше нуля. В тепловом движении участвует лишь небольшое число электронов, например при комнатной температуре Т»300 К и температуре вырождения T ₀=3×10⁴ К, — это 10^–5 от общего числа электронов.

Если (Е–Е_F)>> kТ («хвост» функции распределения), то единицей в знаменателе можно пренебречь по сравнению с экспонентой и тогда распределение Фер­ми — Дирака переходит в распределение Максвелла — Больцмана. Таким образом, при (Е–Е_F)>> kT, т.е. при больших значениях энергии, к электронам в металле применима классическая статистика, в то же время, когда (Е–Е_F)<< kT, к ним примени­ма только квантовая статистика Ферми — Дирака.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: