 |
Рис. 29. Центр масс вертолета (точка «0») и вектор скорости
|
|
|
|
Рис. 29. Центр масс вертолета (точка «0») и вектор скорости
- провести оси ОXg и ОYg нормальной системы координат
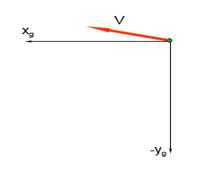
Рис. 30. Оси ОXg и ОYg нормальной системы координат
- провести оси ОXa и ОYа скоростной системы координат. Показать угол наклона траектории θ. Ось ОXa целесообразно проводить в обе стороны от точки 0, ось ОYа – в нижнем (отрицательном) направлении;

Рис. 31. Оси ОXa и ОYа скоростной системы координат. Угол
наклона траектории θ.
- провести оси связанной системы координат ОX и ОY. Показать угол тангажа. При изображении осей учитывать значение угла тангажа на данном режиме. При наклонном наборе Н 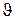 < 0, следовательно ось ОX должна проходить ниже оси ОXg.
< 0, следовательно ось ОX должна проходить ниже оси ОXg.
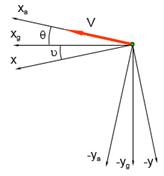
Рис. 32. Оси связанной системы координат ОX и ОY. Угол тангажа.
- показать ось вала несущего винта и угловую скорость его вращения;
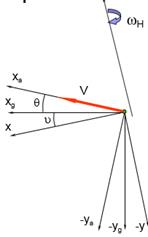
Рис. 33. Ось вращения вала несущего винта
- изобразить силуэт вертолета. Втулку несущего винта изображать сзади оси ОY;
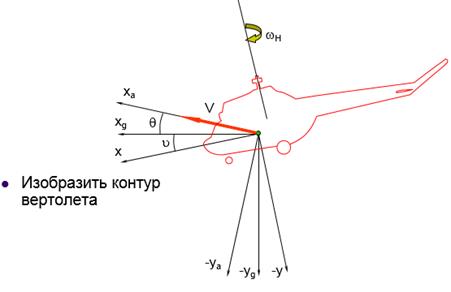
Рис. 34. Контур вертолета
- показать силы  ,
,  . Сила тяжести направлена вертикально вниз;
. Сила тяжести направлена вертикально вниз; 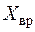 – всегда против направления вектора скорости (изображается над осью ОXa);
– всегда против направления вектора скорости (изображается над осью ОXa);

Рис. 35. Сила тяжести и вредного сопротивления вертолета
- показать силы 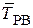 ,
, 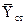 .
.  в моторном полете направлена влево и на виде сбоку проектируется в точку; Yст в моторном полете направлена вниз (параллельно оси ОY).
в моторном полете направлена влево и на виде сбоку проектируется в точку; Yст в моторном полете направлена вниз (параллельно оси ОY).

Рис. 36 Сила тяги рулевого винта и номальная сила стабилизатора
Найти силу тяги несущего винта Тнв как результирующую от сил G и Хвр, но направленную в противоположную сторону. На моторном режиме вектор тяги НВ должен располагаться за осью ОY. Провести вектор 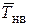 из центра втулки НВ параллельно результирующей от
из центра втулки НВ параллельно результирующей от 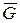 и
и 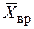 . Показать конус вращения НВ так, чтобы его основание было перпендикулярно силе
. Показать конус вращения НВ так, чтобы его основание было перпендикулярно силе 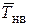 ;
;
|
|
|
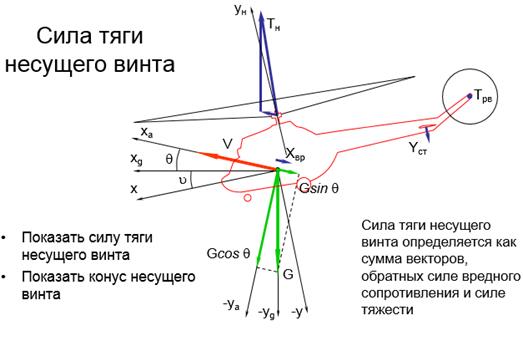
Рис. 37. Сила тяги несущего винта
- найти проекции силы 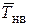 на скоростные оси;
на скоростные оси;
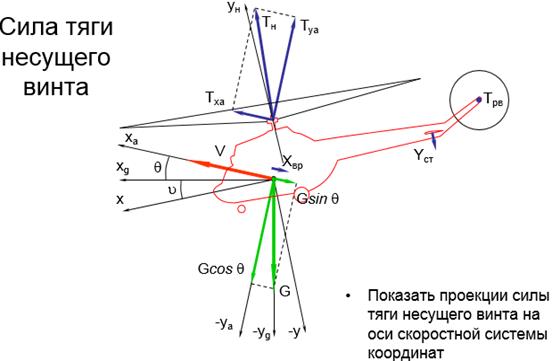
Рис. 38. Проекции силы тяги несущего винта
- показать плечи от линий действий сил 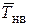 ,
, 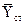 и
и 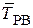 до центра масс вертолета;
до центра масс вертолета;
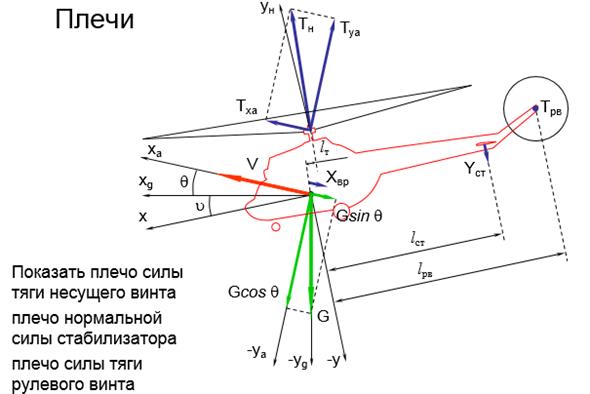
Рис. 39. Плечи сил
- показать моменты МРнв, МZгш, МРрв;

Рис. 40. Моменты, действующие на вертолет

Рис. 41. Схема сил и моментов продольного равновесия вертолета
б) на виде сзади.
Силы будем изображать с учетом направления взгляда, т. е. смотрим на вертолет сзади по оси ОXa скоростной системы координат, а силуэт вертолета (вид сзади) изобразим по оси ОX связанной системы координат:
- показать центр масс вертолета, провести оси ОY и ОZ. Изобразить силуэт вертолета;
- показать силу веса 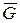 , либо ее составляющую (проекцию) на отрицательное направление оси ОY;
, либо ее составляющую (проекцию) на отрицательное направление оси ОY;
- показать силы  и
и  (
(  =
=  – при γ = 0);
– при γ = 0);
- показать силу 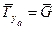 , либо составляющей силы веса;
, либо составляющей силы веса;
- определить ТНВ, как результирующую от 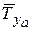 и
и  , показать конус НВ;
, показать конус НВ;
- показать моменты МХгш, МРнв;
- показать плечи от линий действия сил 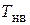 (ат),
(ат), 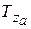 (Ут),
(Ут),  (hРВ).
(hРВ).
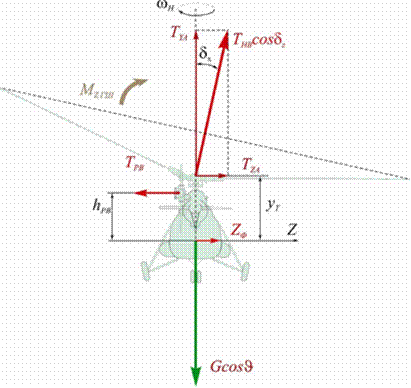
Рис. 42. Схема сил и моментов бокового равновесия вертолета
Аналогично строятся схемы сил для других режимов полета.
Для анализа движения вертолета необходимо уметь записывать уравнения движения.
1. 5 Уравнения движения вертолета
Найдя проекции всех сил, действующих на вертолет в полете на скоростные оси координат, можно оценить характер движения вертолета вдоль каждой оси. Согласно второго закона механики, тело находится в состоянии покоя или прямолинейного движения, если все силы, действующие вдоль данной оси уравновешивают друг друга. Так вдоль оси ОXa действуют силы: –G sinθ, –  , ТХa. Если они уравновешивают друг друга, то ускорение вертолета относительно оси ОXa – отсутствует, движение будет установившееся.
, ТХa. Если они уравновешивают друг друга, то ускорение вертолета относительно оси ОXa – отсутствует, движение будет установившееся.
|
|
|
В общем виде уравнение движения центра масс вертолета записывается в виде:
 , (1. 11)
, (1. 11)
где m – масса вертолета;
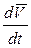 – ускорение центра масс;
– ускорение центра масс;
 – суммарный вектор внешних сил;
– суммарный вектор внешних сил;
 – суммарный вектор всех аэродинамических сил, действующих на вертолет;
– суммарный вектор всех аэродинамических сил, действующих на вертолет;
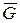 – сила тяжести вертолета.
– сила тяжести вертолета.
При  и
и  – установившееся движение.
– установившееся движение.
Уравнение (1. 11) записывается в виде
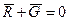 . (1. 12)
. (1. 12)
Для анализа движения вертолета рассмотрим уравнение (1. 12) в проекциях на оси скоростной системы координат (рис. 32 и 33).
|
|
|


