Установившееся движение. Неустановившееся движение. 1.6 Перегрузка. Уравнения движения в перегрузках

Установившееся движение

	;	(1. 13)
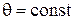	;	(1. 14)
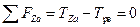
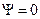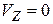	, .	(1. 15)

Неустановившееся движение

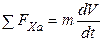
	V ≠ const;	(1. 16)
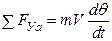
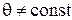	;	(1. 17)
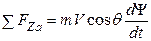
	Ψ ≠ 0, VZ ≠ 0.	(1. 18)

 

(1. 13) – определяет темп и характер изменения скорости полета по величине.

(1. 14) – определяет темп и характер изменения угла наклона траектории, т. е. изменение скорости полета по направлению.

При  угол наклона траектории увеличивается.

(1. 15) – определяет темп изменения скорости смещения относительно оси ОZ_a, а также темп изменения угла рыскания Ψ.

Под действием моментов от сил, действующих на вертолет, он вращается вокруг центра масс (ц. м. ). Вращение вокруг ц. м. на основании закона о моменте количества движения, описывается уравнением:

,                                       (1. 19)

где  – главный суммарный момент относительно центра масс от всех аэродинамических сил, действующих на вертолет;

 – момент инерции вертолета относительно оси вращения;

 – угловая скорость (угловое ускорение) вертолета при вращении относительно центра масс.

Используя уравнение (1. 19) и схему сил и моментов, запишем уравнения моментов относительно осей связанной системы координат:

 

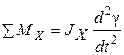	;	(1. 20)
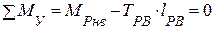
	;	(1. 21)
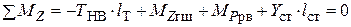
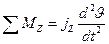	.	(1. 22)

 

Если правая часть уравнений моментов равна 0, то это говорит о постоянстве углового положения вертолета в пространстве.

Если , то .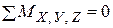

Если 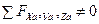, то тогда  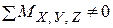и каждое из уравнений моментов характеризуют:

(1. 20) – темп изменения угла крена;

(1. 21) – темп изменения угла рысканья (магнитного курса);

(1. 22) – темп изменения угла тангажа.

Таким образом, уравнения (1. 16 – 1. 18) характеризуют движение вертолета по траектории, а уравнение (1. 20 – 1. 22) характеризуют пространственное положение вертолета.

1. 6 Перегрузка. Уравнения движения в перегрузках

При действии на вертолет внешней неуравновешенной силы, возникает ускорение, т. е. изменение скорости в направлении действия этой силы.

При наличии ускорения возникают силы инерции, направленные противоположно ускорению (неуравновешенной силе). Свойство инерции присуще как вертолету в целом, так и каждой отдельной его части. Поэтому при разгоне, торможении вертолета или криволинейном маневре внешняя сила, вызывающая ускорение вертолета, вызывает такое же ускорение и всех размещенных в нем грузов. Сила инерции груза представляет собой сопротивление его массы изменению скорости движения. Эта сила действует на опору груза, которая в покое при постоянной 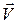 воспринимает только его силу тяжести. Следовательно, при наличии ускорения опора испытывает со стороны груза силу, отличающуюся от его силы тяжести. Для определения насколько возрастет или уменьшится сила действия груза на опору по сравнению с его силой веса, необходимо сравнить неуравновешенную (аэродинамическую) силу с силой тяжести. Так возникает понятие «перегрузка».

Перегрузкой вертолета  в полете называется отношение результирующей всех аэродинамических сил к величине силы тяжести вертолета:

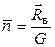 .                                                   (1. 23)

Направление перегрузки соответствует направлению силы 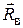, поэтому вектор перегрузки может быть спроектирован на соответствующие оси скоростной системы координат.

Эти проекции называются:

- на ось ОХ_а – тангенциальная перегрузка 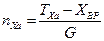;                 (1. 24)

- на ось OY_a – нормальная скоростная перегрузка ;             (1. 25)

- на ось ОZ_а – боковая перегрузка .                                  (1. 26)

Из выражений (1. 24 – 1. 26) видно, что та или иная перегрузка зависит только от величины проекций аэродинамических сил на соответствующие оси.

Знак перегрузки соответствует ее направлению вдоль оси.

Выражение (1. 24) характеризует темп разгона или торможения вертолета по оси ОХ_а.

Если:  Т_Ха > Х_ВР → n_Ха > 0   –     разгон скорости;

      Т_Ха < Х_ВР → n_Ха < 0  –     торможение;

      Т_Ха = Х_ВР → n_Ха = 0  –     установившийся полет.

Максимальное значение 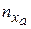 ограничивается возможностями силовой установки и прочностью несущего винта.

Минимальное значение 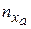 не должно превышать значения  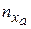£ 0, 5. Ограничение связано с возможностью раскрутки НВ при торможении и выходом на недопустимые обороты.

Выражения (1. 25) и (1. 26) – характеризует темп изменения скорости по направлению, т. е. искривление траектории движения вертолета или степень нагруженности элементов конструкции вертолета.

Нормальная ( 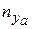) перегрузка является основной в определении маневренных свойств вертолета, так как может достигать значительных величин по отношению к  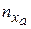и 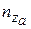. С целью обеспечения безопасности полетов на нормальную перегрузку накладывается ряд ограничений:

- разрушающая перегрузка  – ее получают расчетным путем при статистических испытаниях вертолета на прочность. Для большинства транспортных вертолетов  = 3 – 4, 5;

- максимальная эксплуатационная перегрузка 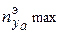 (максимально-допустимая кратковременная при эксплуатации вертолета). Ее величина ограничена прочностью конструкции лопастей НВ и вертолета в целом:

 ,                                           (1. 27)

где К = 1, 5 – коэффициент запаса прочности;

- располагаемая перегрузка, которая может быть получена при маневрировании, она подразделяется на:

-  – максимальная (длительная) перегрузка в эксплуатации. Для вертолета Ми-8 =1, 5. Ее значение ограничено главным образом по прочности лопастей НВ и по взлетной мощности двигателей. Достигается при выполнении установившегося виража с максимально возможным креном;

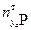-  – кратковременная располагаемая перегрузка. Может быть достигнута в процессе маневрирования за счет увеличения угла атаки НВ и увеличения общего шага до максимального значения при сохранении оборотов НВ. Она зависит от полетной массы вертолета и будет тем больше, чем меньше полетная масса. При выходе на  возможно ухудшение устойчивости и управляемости вертолета из-за срывных явлений на лопастях НВ. Для Ми-8  = 2. 0.

Располагаемые перегрузки разрешается использовать в полной мере, если они не превосходят допустимые.

Уравнение (1. 22) – боковая перегрузка 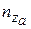. Больших значений не достигает, даже когда силы по оси ОZ_а направлены в одну сторону (Т_Zа + Т_рв), что возможно при левом скольжении –  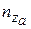= (0, 15 + 0, 2) n_Удоп. . Однако достижение максимального значения  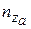за счет создания энергичного скольжения запрещается из-за возникновения значительных напряжений на хвостовой балке и рулевом винте.

Действие перегрузок летчик ощущает по направлению осей связанной системы координат, т. е. по расположению сидения летчика в кабине.

Учитывая, что оси связанной системы координат повернуты относительно скоростной системы на углы атаки α _ф и скольжения β, можно определить связь между составляющими перегрузки в этих системах координат. Если β = 0, эта связь будет иметь вид:

n_Xа = n_X · cosα _Ф – n_У · sinα _Ф;                                                    (1. 28)

n_Уа = n_У · cosα _Ф + n_X · sinα _Ф;                                                    (1. 29)

n_Zа = n_Z = 0.                                               (1. 30)

Проекции вектора перегрузки в связанной системе координат называются:

- n_X – продольная перегрузка,

- n_У – нормальная перегрузка,

- n_Z – поперечная перегрузка.

Уравнения движения в перегрузках можно получить, разделив  выражение (1. 13…1. 18) на величину силы тяжести вертолета G:

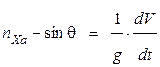;                                             (1. 31)

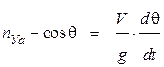;                                             (1. 32)

 .                                           (1. 33)

Из данных уравнений видно, что от перегрузки 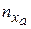 зависит темп изменения скорости полета по величине, а от  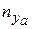и 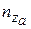 – темп изменения скорости по направлению.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: