Оптика..   Номера задач по порядку

Оптика.

Таблица вариантов

Таблица вариантов	Номера задач по порядку

Примеры решения задач.

Пример1. На толстую стеклянную пластину с показателем преломления n₃=1, 5, покрытую очень тонкой пленкой (n₂=1, 4), падает нормально пучок монохроматического света (l=0, 6 мкм). Отраженный свет максимально ослаблен вследствие интерференции. Определить толщину пленки (n₁=1).

 

Решение:

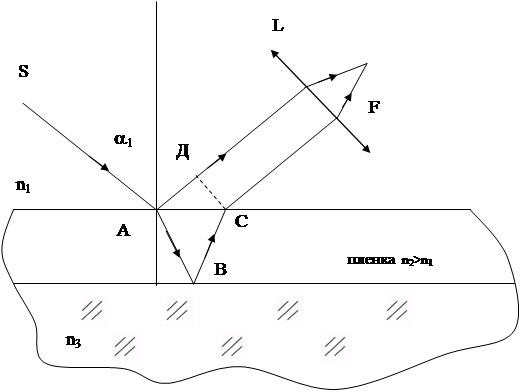
Из волны, падающей на пленку, выделяем узкий пучок S.

Ход этого пучка в случае, когда a1¹ 0, показан на рисунке. В точках А и В падающий пучок частично отражается и частично преломляется. Отраженные пучки света падают на собирающую линзу L, пересекаются в ее фокусе и интерферируют между собой. Изменение фазы интерферирующих лучей по отношению друг к другу не будет, так как n₃> n₂> n₁. Известно, что условие максимального ослабления света состоит в том, что 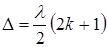, из рисунка видно, что оптическая разность хода

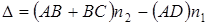
Следовательно условие min примет вид

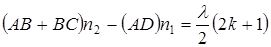
Если угол падения a₁ будет уменьшаться ® 0 то и АД ® 0 и АВ+ВС® 2d, где d – толщина пленки. При a₁ = 0 получим

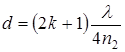
Полагая, что к =0, 1, 2, 3......, получим ряд возможных значений толщины пленки. Например d=0. 33мкм.

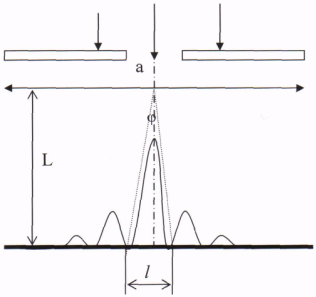
Пример 2. На щель шириной а=0. 1мм нормально падает параллельный пучок монохроматического света (l = 0. 6мкм). Определить ширину L центрального максимума в дифракционной картине, полученной с помощью линзы, располагающейся непосредственно за щелью. Экран отстоит от линзы на расстояние 1м.

Решение:

Расстояние между двумя min - ширина максимума. Min интенсивности света при дифракции от одной щели наблюдаются под углами определяемыми условием 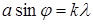, где k - порядок min (k=1). Расстояние между двумя min определим из чертежа  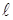= 2Ltgj, при малых углах tgj = j = sinj=> 1 = 2Lsinj =>  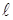= 2Lkl/a=1. 2 см.

Пример 3. Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света составляет угол j=97° с падающим пучком. Определить показатель преломления n₁ жидкости, если отраженный свет полностью поляризован.

 

Согласно закону Брюстера, в случае полностью поляризованного отраженного света:                       

j

tga=n₂₁, где .

Согласно условию отраженный луч повернут на угол j относительно падающего луча. Так как угол падения равен углу отражения, то

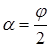 и, следовательно, 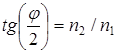, откуда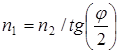

Пример 4. Длина волны l_mах, на которую приходится максимум энергии в спектре излучения черного тела, равна 0, 58 мкм. Определить максимальную спектральную плотность энергетической светимости / М_l т_max/, рассчитанную на интервал длин волн Dl 1 нм, вблизи l_mах.

Решение. Максимальная спектральная плотность энергетической светимости пропорциональна пятой степени температуры Кельвина и выражается формулой 

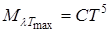                                     (1)

 

Температуру Т выразим из закона смешения Вина          

l_mах = b/Т.

Подставим полученное выражение температуры в формулу (1), найдем

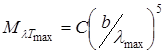
Подставив все данные, включая табличные, получим ответ.

Пример 5. Определить красную границу l₀фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны l максимальная скорость v_maх фотоэлектронов равна 0, 65 Мм/с.

Решение. При облучении светом с l₀, соответствующей красной границе фотоэффекта, скорость, а также и кинетическая энергия фотоэлектронов равна 0. Поэтому уравнение Эйнштейна для фотоэффекта Е= А+Т в случае красной границы запишется в виде Е = А или

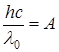; отсюда  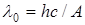                                                   (1)

Работа выхода для цезия

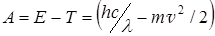                           (2)

Подставив все данные и табличные значения, получим А = 3, 05× 10^-19 Дж. Для определения красной границы фотоэффекта подставим значение А, h и с в формулу (1) и вычислим l₀ = 651 нм.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: