Примеры решения задач

Пример 1. Заряды q₁=5 нКл и q₂ = 4 нКл находятся в двух вершинах равностороннего треугольника со стороной r=0. 2 м. Найти потенциал и напряженность в третьей вершине треугольника (принять e = 1)

         

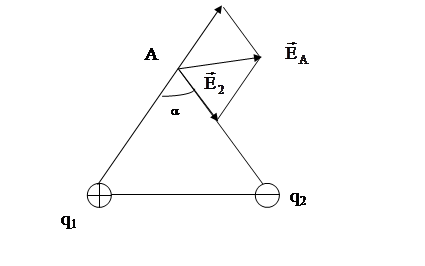
Решение: по принципу суперпозиции напряженность поля системы двух зарядов в точке равна векторной сумме напряженности полей, создаваемых каждым из зарядов в данной точке в отдельности.

Построим векторы 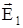 и  напряжённости полей, создаваемых каждым из

зарядов в т А. Вектор 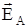 равен векторной сумме  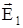и

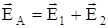
По условию задачи угол между 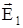 и составляет 120°, значит другой угол параллелограмма, образованного 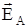,  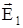и  равен 60°. Следовательно, по теореме косинусов:

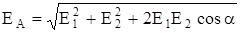
Учитывая, что 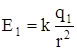  и 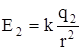, a = 60°. Получим

Подставив численные значения, получим искомую величину напряженности поля в т. А:

Е_А = 1030 В/м

Теперь найдем потенциал поля двух зарядов в т. А. Он равен алгебраической сумме потенциалов поля от каждого заряда:

j_А=j₁+j₂, где j₁и j₂ - потенциалы полей, создаваемые зарядами q₁ и q₂ соответственно

, ,

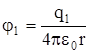следовательно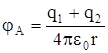                 

Подставив численные значения, получим: j_А = 45 В

 

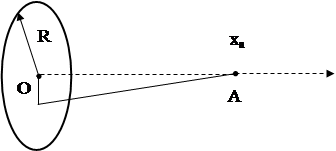
Пример 2. По находящейся в вакууме очень тонкой круглой пластине радиусом R= 120 мм, равномерно распределен заряд 1. 8 мкКл. Приняв ось пластинки за ось X, найти потенциал точек лежащих на оси как функцию X и вычислить j в точке Ха = 80 мм.

			х

 

 

 

Решение: запишем выражение для потенциала в точке на оси X, создаваемого совокупностью зарядов на круглой пластинке. Каждый точечный заряд расположен в точке на пластине на расстоянии г от точки О ( центра круга ), а расстояние от этого заряда до точки на оси X равно:

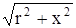
Потенциал поля, создаваемый зарядами пластины в точке х. равен:

 ,

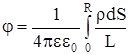где 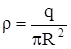- поверхностная плотность заряда на пластинке.

Учитывая, что , а dS = d(pr²)

Получим

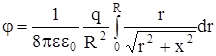
Подставив выражение для табличного интеграла, получим:

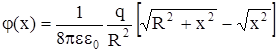
Для точки А подставим Х=Ха=0. 08 м, получим j_А = 3× 10⁴ В.

 

Пример 3. Электрическое поле создано тонкой бесконечно длинной равномерно заряженной нитью, с линейной плотностью заряда t =3О нКл/м. На расстоянии а=20 см от нити находится круглая площадка радиусом г =1 см. Определить поток вектора напряженности через эту площадку, если её плоскость составляет угол b =30° с линией напряженности, проходящей через эту площадку.

 

 

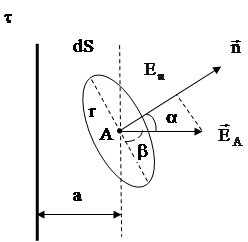Решение: Поле нити неоднородно. Поток вектора напряженности этого поля будет равен

,

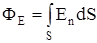где E_n – проекция вектора Е на нормаль к площадке и

,

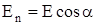Тогда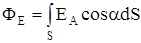                            

Так как размеры площадки dS малы по сравнению с расстоянием до нити, то напряженность мало меняется в пределах площадки по величине и направлению, поэтому будем брать средние значения напряженности и косинуса угла. Тогда:

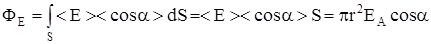
Для поля длинной равномерно заряженной нити:

, ,

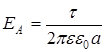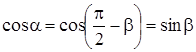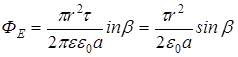
Подставим числовые значения и получим: Ф_Е = 424 мВм

 

Пример 4. Расстояние между пластинами конденсатора d =5см. Напряженность электростатического поля внутри него Е=2000 В/м. Электрон летит вдоль одной из силовых линий от одной пластины к другой. Начальная скорость электрона равна нулю. Какую скорость приобрел электрон на этом пути за счет работы сил электростатического поля.

Решение: Работа сил электростатического поля при движении электрона:

 

По закону сохранения энергии

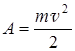или ,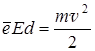

следовательно скорость электрона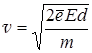

Численное значение скорости =5. 9× 10⁶ м/с.

 

Пример 5. Два одинаковых плоских конденсатора соединены параллельно и заряжены до разности потенциалов U1=100 В. Определить разность потенциалов на конденсаторах U 2, если после отключения их от источника питания расстояние между пластинами второго конденсатора уменьшили в два раза.

Решение.

Для параллельного соединения конденсаторов: С_общ = С₁ + С₂ и q _общ. =q₁+q₂.

Для батареи конденсаторов:

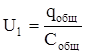
Воспользуемся формулой для плоского конденсатора и, учитывая то, что у нас два одинаковых конденсатора, запишем их общий заряд в следующем виде:

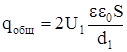
После отключения от источника заряд батареи остается неизменным, поэтому: q'_общ = q_общ, а емкость первого конденсатора перепишется в виде:

, т. к. 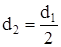, тогда

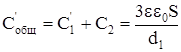
и                                     

Следовательно: .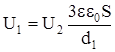

Получаем: .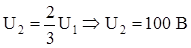

Пример 5. При разрядке плоского воздушного конденсатора выделилось количество теплоты Q=4. 19 мДж. Определить каким было напряжение на конденсаторе, если площадь его пластин S =0. 01 м², а расстояние между ними d=5 мм.

Решение:

Энергия конденсатора:

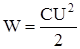
По условию задачи вся энергия перешла в теплоту, т. е Q=W.   

Отсюда                          ,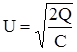

где                                       .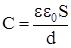

Следовательно:

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: