 |
Механические колебания и волны
|
|
|
|
Механические колебания и волны
Таблица вариантов
| Номера вариантов | Номера задач по порядку | ||||
| 1 | 25 | 37 | 49 | ||
| 2 | 26 | 38 | 50 | ||
| 3 | 15 | 27 | 39 | 51 | |
| 5 | 41 | 77 | |||
| 6 | 18 | 30 | 78 | ||
| 7 | |||||
| 32 | 80 | ||||
| 9 | 21 | 33 | |||
| 22 | 34 | 46 | 2 | ||
| 35 | 47 | 3 | |||
| 12 | 12 | 24 | 36 | 4 | |
| 52 | 71 | 26 | |||
| 53 | 72 | 27 | |||
| 15 | 73 | 28 | |||
| 16 | 65 | 74 | 24 | ||
| 56 | 75 | 30 | |||
| 57 | 67 | 48 | 31 | 22 | |
| 68 | 47 | 21 | |||
| 69 | 19 | ||||
| 70 | 34 | 37 | |||
| 61 | 24 | 35 | 38 | ||
| 12 | 36 | 39 | |||
| 22 | 71 | 40 | |||
| 21 | 41 | 72 | 80 | ||
| 9 | 40 | 73 | |||
| 39 | 74 | 50 | |||
| 7 | 18 | 38 | 75 | 51 | |
| 6 | 37 | 76 | 49 | ||
| 5 | 16 | 77 | 48 | ||
Примеры решения задач
Пример №1. Амплитуда гармонического колебания А = 5 см, период Т = 4 с. Найти максимальную скорость и максимальное ускорение колеблющейся точки.
| Дано | Решение |
| А = 5 см Т = 4 с | Уравнение движения имеет вид
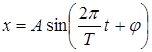
|
| υ max -? amax -? | Скорость и ускорение точки, совершающей колебания, определяются соотношениями |
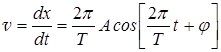
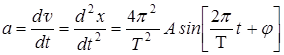
Они имеют максимальное значение при равенстве cos и sin ±1.
Поэтому: 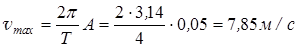
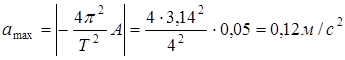
Пример №2. Уравнение колебаний материальной точки массой m = 10 г имеет вид  см. Найти максимальную силу Fmax, действующую на точку и полную энергию W колеблющейся точки.
см. Найти максимальную силу Fmax, действующую на точку и полную энергию W колеблющейся точки.
| Дано | Решение | ||
m= 10 г
 см см
| Так как уравнение колебаний имеет вид
| ||
| Fmax -? W -? |
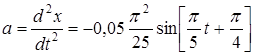 , м/с2
, м/с2
Сила, под действием которой точка массой m совершает гармонические колебания
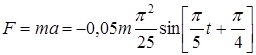
Тогда максимальная сила, действующая на точку
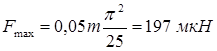
Кинетическая энергия материальной точки равна
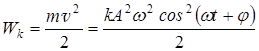
Потенциальная энергия материальной точки
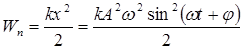
а так как k = mw2, то 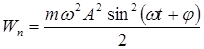
При этом за нулевой уровень отсчета потенциальной энергии выбирается положение равновесия х = 0. Полная энергия колеблющейся точки
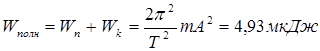
Пример №З. К пружине подвешен груз массой m =10 кг. Зная, что пружина под влиянием силы F=9, 8Н растягивается на расстояние 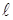 = 1, 5 см, найти период Т вертикальных колебаний груза
= 1, 5 см, найти период Т вертикальных колебаний груза
| Дано | Решение |
m= 10 кг
F = 9, 8 Н
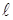 = 1, 5 см = 1, 5 см
|
По закону Гука сила упругости F =-кх. (Знак минус говорит о том что это возвращающая сила), откуда |
| Т -? |
Уравнение второго закона Ньютона для груза имеет вид
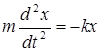
Введя обозначение 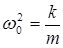 , получим дифференциальное уравнение
, получим дифференциальное уравнение
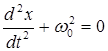 ,
,
где 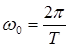 - циклическая частота колебаний.
- циклическая частота колебаний.
Период колебаний вертикального пружинного маятника
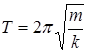 ,
,
решая уравнение, получим

Пример №4. Найти амплитуду А и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями
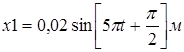 и
и 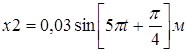
Решение:
Из уравнений колебаний находим, что А1 = 0, 02 м и А2 = 0, 03 м и их начальные фазы 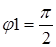 и
и  .
.
При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой
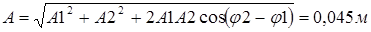
Начальная фаза определяется из уравнения
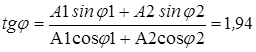 , тогда j = arctg 1, 94 = 62, 75°
, тогда j = arctg 1, 94 = 62, 75°
Пример №5. Точка участвует в двух взаимно перпендикулярных колебаниях
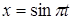 и
и 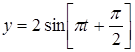 .
.
Найти траекторию результирующего колебания.
Решение:
При сложении двух взаимно перпендикулярных колебаний материальной точки, имеющих уравнения
 и
и 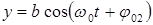 ,
,
траектория результирующего колебания описывается уравнением
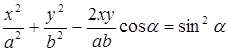 ,
,
где 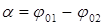 - разность фаз складываемых колебаний. Мы имеем а =1, b = 2,
- разность фаз складываемых колебаний. Мы имеем а =1, b = 2, 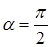 .
.
|
|
|
Подставляя числовые значения, получим
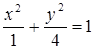 ,
,
т. е. траектория - эллипс.
Пример 6. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания d = 0, 2. Во сколько раз уменьшится ускорение маятника в его крайнем положении за одно колебание?
| Дано | Решение |
| d = 0, 2 | Уравнение затухающего колебания имеет вид:
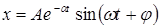
|
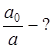
| Для нахождения скорости продифференцируем это выражение по времени: |
 ,
,
тогда
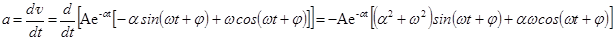
тогда 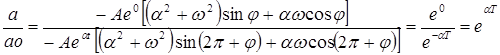
Логарифмический декремент затухания равен
d = aТ, тогда 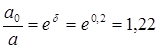
Задачи для самостоятельного решения
1. Написать уравнение гармонического колебательного движения с амплитудой А = 5 см, если за время t=1мин совершается 150 колебаний и начальная фаза колебаний 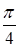 .
.
2. Написать уравнение гармонического колебательного движения с амплитудой А = 0, 1м, периодом Т= 4 с и начальной фазой j = 0.
3. Написать уравнение гармонического колебательного движения с ампли-тудой А = 50 мм, периодом Т= 4 с и начальной фазой колебаний 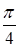
Найти смещение х колеблющейся точки от положения равновесия при t = 0 и t = 1, 5 с.
4. Написать уравнение гармонического колебательного движения с амплитудой А = 5 см, периодом Т= 8 с если начальная фаза колебаний равна
а)0; б) 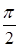 ; в)p; г)
; в)p; г) 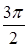 ; д)2p.
; д)2p.
5. Через какое время от начала движения точка, совершающая гармо-ническое колебание, сместится от положения равновесия на половину амплитуды? Период колебания Т = 24 с, начальная фаза колебаний j = 0.
6. Начальная фаза гармонического колебания j = 0. Через какую долю периода скорость точки будет равна половине её максимальной скорости?
7. Через какое время от начала движения точка, совершающая колебательное движение по закону 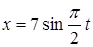 , проходит путь от положения равновесия до максимального смещения?
, проходит путь от положения равновесия до максимального смещения?
8. Уравнение колебания точки 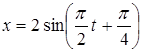 см. Найти период колебания Т, максимальную скорость и максимальное ускорение точки.
см. Найти период колебания Т, максимальную скорость и максимальное ускорение точки.
9. Уравнение колебания точки 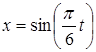 . Найти момент времени, в
. Найти момент времени, в
который достигаются максимальная скорость и максимальное ускорение.
10. Точка совершает гармоническое колебание. Период колебания Т=2с, амплитуда А=50мм., начальная фаза j = 0. Найти скорость точки в момент времени, когда смещение точки от положения равновесия х = 25 мм.
|
|
|
11. Написать уравнение гармонического колебательного движения если максимальное ускорение точки 49, 3 см/с2, период колебаний Т= 2 с и смещение точки от положения равновесия в начальный момент времени х0 = 25 мм.
12. Начальная фаза гармонического колебания j = 0. При смещении точки от положения равновесия x1 =2, 4 см скорость точки v1=3 см/с, а при смещении х2=2, 8 см скорость точки v1=2 см/с. Найти амплитуду А и период этого колебания.
13. Уравнение колебания материальной точки имеет вид
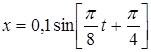 м
м
Найти максимальную силу Fmax, действующую на точку.
14. Уравнение колебания материальной точки массой m =16 г имеет вид
 см
см
Найти значения кинетической Wк, потенциальной Wп и полной энергии точки Wполн в момент времени t = 2 c.
15. Найти отношение кинетической и потенциальной энергии точки, совершающей гармоническое колебание для моментов времени а)t=Т/12; б. )t=Т/8; в) t=Т/6. Начальная фаза равна нулю.
16. Найти отношение кинетической к потенциальной энергии точки, совершающей гармоническое колебание, для моментов, когда смещение точки от положения равновесия составляет: а) х = А/4, б) х = А/2, в) х = А, где А — амплитуда колебаний.
17. Полная энергия тела, совершающего гармонические колебания равна 30 мкДж. Максимальная сила, действующая на тело Fmах=1, 5 мН. Написать уравнение движения этого тела, если период колебаний Т= 2 с и начальная фаза j= 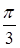 .
.
18. Амплитуда колебаний материальной точки А= 2см. Полная энергия колебаний равна 0, 3 мкДж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 22, 5 мкН.
19. Шарик, подвешенный на нити длинной 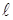 =2 м, отклоняют от положения равновесия на угол 4° и наблюдают его колебания. Полагая колебания незатухающими гармоническими, найти скорость шарика при прохождении им положение равновесия.
=2 м, отклоняют от положения равновесия на угол 4° и наблюдают его колебания. Полагая колебания незатухающими гармоническими, найти скорость шарика при прохождении им положение равновесия.
20. К пружине подвешен груз. Максимальная кинетическая энергия колебаний груза 1Дж. Амплитуда колебаний А = 5см. Найти коэффициент жёсткости пружины.
21. Как изменится период вертикальных колебаний груза, подвешенного на двух пружинах, если от последовательного соединения пружин перейти к параллельному?
|
|
|
22. Медный шарик, подвешенный к пружине, совершает вертикальные гармонические колебания. Как изменится период колебаний, если медный шарик заменить алюминиевым того же радиуса?
23. К пружине подвешена чашка весов с гирями. При этом период вертикальных колебаний Т1 = 0, 5 с. После того как на чашку весов положили добавочные гири, период колебаний стал Т2= 0, 6 с. Насколько удлинилась пружина от прибавления этого добавочного груза?
24. К резиновому шнуру длинной 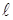 = 40 см и радиусом r = 1 мм подвешена гиря массой m = 0, 5 кг. Зная, что модуль Юнга резины 3 МН/м2, найти период вертикальных колебаний гири. Указание: жёсткость резины, её длина и площадь поперечного сечения связаны с модулем Юнга соотношением
= 40 см и радиусом r = 1 мм подвешена гиря массой m = 0, 5 кг. Зная, что модуль Юнга резины 3 МН/м2, найти период вертикальных колебаний гири. Указание: жёсткость резины, её длина и площадь поперечного сечения связаны с модулем Юнга соотношением 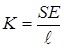
25. Написать уравнение движения, возникающего в результате сложения двух одинаково направленных гармонических колебаний с одинаковым периодом Т= 8 с с одинаковой амплитудой А=0, 02м. Разность фаз между этими колебаниями 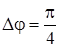 . Начальная фаза одного из колебаний равна нулю.
. Начальная фаза одного из колебаний равна нулю.
26. В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами получается результирующее колебание с тем же периодом и той же амплитудой. Найти разность фаз складываемых колебаний.
27. Найти амплитуду А и начальную фазу j гармонического колебания, получаемого от сложения одинаково направленных колебаний, имеющих уравнения:
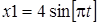 см и
см и 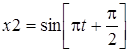 см
см
Написать уравнение результирующего колебания. Дать векторную диаграмму сложения амплитуд.
28. Написать уравнение результирующего колебания, возникающее в результате сложения двух взаимно перпендикулярных колебании с одинаковой частотой 5Гц и одинаковой начальной фазой 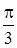 . Амплитуды колебаний равны А1=0, 1м и А2=0, 05м.
. Амплитуды колебаний равны А1=0, 1м и А2=0, 05м.
29. Точка участвует в двух колебаниях одинакового периода с одинаковыми начальными фазами, амплитуды колебаний равны А1= 3 см, А2= 4 см. Найти амплитуду результирующего колебания, если колебания совершаются:
а) в одном направлении, б) в двух взаимно перпендикулярных направлениях..
30. Точка участвует в двух взаимно перпендикулярных колебаниях 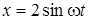 и
и 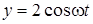 . Найти траекторию движения точки.
. Найти траекторию движения точки.
31. Точка участвует в двух взаимно перпендикулярных колебаниях  и
и 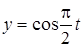 . Найти траекторию движения точки.
. Найти траекторию движения точки.
32. Точка участвует в двух взаимно перпендикулярных колебаниях 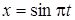 и
и 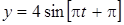 . Найти траекторию движения точки и начертить её с нанесением масштаба.
. Найти траекторию движения точки и начертить её с нанесением масштаба.
33. Период затухающих колебаний Т= 4 с, логарифмический декремент затухания d = 1, 6. Начальная фаза равна нулю. При t =Т/4 смещение точки х = 4, 5см. Написать уравнение этого колебания.
34. Уравнение затухающих колебаний дано в виде: 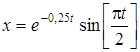 м. Найти скорость v колеблющейся точки в моменты времени t, равные: О, Т, 2Т, ЗТ, 4Т.
м. Найти скорость v колеблющейся точки в моменты времени t, равные: О, Т, 2Т, ЗТ, 4Т.
|
|
|
35. Логарифмический декремент затухания математического маятника d =0. 2. Во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника?
36. Найти логарифмический декремент затухания d математического маятника, если за 1мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника 1м.
37. Математический маятник длиной 24, 7см совершает затухающие колебания.
Через какое время энергия колебаний маятника уменьшится в 9. 4 раза?
Задачу решать для значений логарифмического декремента затухания:
а) d =0, 01; 6) d =1.
38. Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за 3 мин?
39. Математический маятник длиной ЕЙ). 5м, выведенный из положения равновесия, отклонился при первом колебании на х1=5см, а при втором ( в ту же сторону ) - на х2=4см. Найти время, в течении которого амплитуда уменьшится в е раз (е =2. 72).
40. К вертикально висящей пружине подвешивают груз. При этом пружина удлиняется на 9, 8 см. Оттягивая этот груз вниз, и, отпуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания, чтобы колебания прекратились через 10 с. (Считать, что колебания прекратились, если их амплитуда упала до значения, составляющего 1% от начальной амплитуды).
41. См. задачу 40. Каким должен быть коэффициент затухания, чтобы логарифмический декремент затухания был равен 6?
42. Тело с массой m = 10 г совершает затухающие колебания с максимальной амплитудой Амах = 7см, начальной фазой равной нулю, и коэффициентом затухания 1, 6 с -1. На тело начала действовать внешняя периодическая сила F, под действием которой установились вынужденные колебания. Уравнение вынужденных колебаний имеет вид: 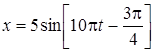 см. Найти уравнение собственных колебаний и уравнение внешней периодической силы.
см. Найти уравнение собственных колебаний и уравнение внешней периодической силы.
43. По грунтовой дороге прошел трактор, оставив следы в виде ряда углублений, находящихся на расстоянии 30см друг от друга. По этой дороге покатили детскую коляску, имеющую две одинаковые рессоры, каждая из которых прогибается на 2 см под действием груза массой 1 кг. С какой скоростью катили коляску, если от толчков на углублениях она, попав в резонанс, начала сильно раскачиваться? Масса коляски 10 кг.
44. Найти длину волны l колебания, период которого Т=10-14 с. Скорость распространения колебаний с=3× 108 м/с.
45. Звуковые колебания, имеющие частоту n=500Гц и амплитуду А=0, 25мм, распространяются в воздухе. Длинна волны l=70см. Найти скорость распространения колебаний и максимальную скорость частиц воздуха.
46. Уравнение незатухающих колебаний имеет вид  см. Найти уравнение волны, если скорость распространения колебаний 300 м/с. Написать уравнение колебаний для точки, отстоящей на расстоянии 600 м от источника колебаний. Написать уравнение колебания для точек волны в момент времени t =4 с после начала колебаний.
см. Найти уравнение волны, если скорость распространения колебаний 300 м/с. Написать уравнение колебаний для точки, отстоящей на расстоянии 600 м от источника колебаний. Написать уравнение колебания для точек волны в момент времени t =4 с после начала колебаний.
47. Уравнение незатухающих колебаний имеет вид  см. Найти смещение х от положения равновесия точки, находящейся на расстоянии 75см от источника колебаний, для момента времени t= 0. 01 с после начала колебаний. Скорость распространения колебаний с = 300м/с.
см. Найти смещение х от положения равновесия точки, находящейся на расстоянии 75см от источника колебаний, для момента времени t= 0. 01 с после начала колебаний. Скорость распространения колебаний с = 300м/с.
48. Уравнение незатухающих колебаний имеет вид 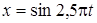 см. Найти смещение х от положения равновесия, скорость и ускорение точки, находящейся на расстоянии 20см от источника колебаний, для момента времени t=1 с после начала колебаний. Скорость распространения с = 300м/с.
см. Найти смещение х от положения равновесия, скорость и ускорение точки, находящейся на расстоянии 20см от источника колебаний, для момента времени t=1 с после начала колебаний. Скорость распространения с = 300м/с.
49. Найти разность фаз колебаний двух точек, отстоящих от источника колебаний на расстояния 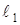 =10м и
=10м и 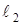 = 16м. Период колебаний Т= 0. 04с. Скорость распространения колебаний с = 300м/с.
= 16м. Период колебаний Т= 0. 04с. Скорость распространения колебаний с = 300м/с.
50. Найти разность фаз колебаний двух точек, лежащих на луче и отстоящих на расстоянии 2 м друг от друга, если длина волны l =1 м.
51. Найти смещение х от положения равновесия точки, отстоящей от источника колебаний на расстояние 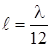 , для момента времени t=Т/6.
, для момента времени t=Т/6.
Амплитуда колебаний А = 0, 05м.
52. Смещение от положения равновесия точки, отстоящей от источника колебаний на расстояние 4см, в момент времени t=Т/6 равно половине амплитуды. Найти длину бегущей волны.
53. Уравнение колебаний имеет вид 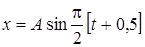 . Определить период и начальную фазу колебаний.
. Определить период и начальную фазу колебаний.
54. Определить период, частоту, начальную фазу колебаний, заданных уравнением 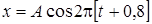 .
.
55. Точка совершает колебания по закону 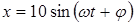 см. Определить начальную фазу, если 1) х=5 см, v> 0, t> 0; 2) х=-5 см, v< 0, t=0.
см. Определить начальную фазу, если 1) х=5 см, v> 0, t> 0; 2) х=-5 см, v< 0, t=0.
56. Точка совершает колебания с амплитудой 5см и периодом 1, 4с. Написать уравнение этих колебаний, считая, что при t=0 х=0 и v< 0.
57. Точка равномерно движется по окружности по часовой стрелке с периодом 5с. Диаметр этой окружности равен 15см. Написать уравнение движения проекции точки на ось х, проходящую через центр окружности, если в начальный момент времени проекция на ось х равна нулю. Найти смещение х, скорость v и ускорение проекции точки в момент времени t=5с.
58. Определить максимальное значение скорости и ускорения точки, совершающей гармонические колебания с амплитудой А=1см, и угловой частотой 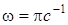 по синусоидальному закону.
по синусоидальному закону.
59. Точка совершает колебания по закону 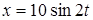 см. Определить ускорение точки в момент времени, когда её скорость v = 10см/с.
см. Определить ускорение точки в момент времени, когда её скорость v = 10см/с.
60. Точка совершает колебания, максимальное смещение точки равно 20см, максимальная скорость v=40см/с. Найти угловую частоту колебаний, период и амплитуду. Написать уравнение колебаний, начальная фаза равна 0.
61. Материальная точка масса m = 50г совершает колебания, уравнение которых имеет вид 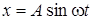 , где А = 5 см, w = 4 с-1. Найти силу, действующую на точку в положении наибольшего смещения точки.
, где А = 5 см, w = 4 с-1. Найти силу, действующую на точку в положении наибольшего смещения точки.
62. Колебания точки происходят по закону 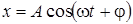 . В некоторый момент времени смещение х= 10см, скорость v=20см/с и ускорение а = 100 см/с2. Найти амплитуду А и фазу колебания в рассмотренный момент времени.
. В некоторый момент времени смещение х= 10см, скорость v=20см/с и ускорение а = 100 см/с2. Найти амплитуду А и фазу колебания в рассмотренный момент времени.
63. Колебания материальной точки массой m = 0. 5г происходят по закону 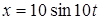 см. Определить максимальные значения возвращающей силы и кинетической энергии.
см. Определить максимальные значения возвращающей силы и кинетической энергии.
64. Найти возвращающую силу в момент времени t=10 с и полную энергию материальной точки, совершающей колебания по закону  см
см
Масса материальной токи 1г.
65. Колебания материальной точки происходят по закону 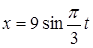 см В момент, когда возвращающая сила достигла значения 10 мН, потенциальная энергия стала равной 200 мкДж. Определить этот момент времени.
см В момент, когда возвращающая сила достигла значения 10 мН, потенциальная энергия стала равной 200 мкДж. Определить этот момент времени.
66. Определить жёсткость пружины к, если к ней подвесили груз массой 500 г, который стал совершать колебания с периодом Т= 2 с.
67. Груз, подвешенный к пружине, колеблется с амплитудой 10см. Определить полную энергию колебаний, если жесткость пружины 1, 5 кН/м.
68. Найти отношение периодов двух математических маятников, если отношение их длин равно 3.
69. Математический маятник длиной 2м установлен в лифте. Лифт опускают с ускорением 1. 5м/с2. Определить период колебания маятника. 70. Однородный диск с радиусом 50см колеблется около горизонтальной оси, проходящей через центр диска. Каков период его колебаний?
71. Амплитуда затухающих колебаний за время t1=10 с уменьшилась в 3 раза. За какое время t2 амплитуда уменьшится в 10 раз?
72. Определить коэффициент затухания маятника, если за время t=15с, амплитуда уменьшилась в 2 раза.
73. Определить логарифмический декремент затухания, если амплитуда маятника длиной 2 м за время t=1 мин уменьшилась втрое.
74. Логарифмический декремент затухания маятника равен 0, 001. Определить число полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась втрое.
75. Груз массой 200г подвешен к пружине жесткостью 10 Н/м и совершает упругие колебания в некоторой среде. Логарифмический декремент затухания 0, 002. Определить число полных колебаний, которые должен сделать груз, чтобы амплитуда колебаний уменьшилась в 1, 5 раза. За какое время t пройдет это изменение?
76. Один из маятников за некоторое время совершил 10 колебаний. Другой за это же время совершил 6 колебаний. Длины маятников отличаются друг от друга на 16 см. Определить длины маятников 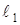 и
и 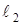 .
.
77. Найти потенциальную энергию математического маятника с массой 200г при отклонении на угол 10° от вертикали, если частота колебаний маятник n=0, 5 с-1. Считать потенциальную энергию маятника в положении равновесия равной нулю.
78. С каким ускорением и в каком направлении должна двигаться кабина лифта, чтобы находящийся в ней секундный маятник за время t =2 мин 30с совершил 300 колебаний?
79. Колебательная система совершает затухающие колебания с частотой n= 400Гц. Определить частоту n0 собственных колебаний, если резонансная частота равна nрез= 99Гц
80. Определить на сколько резонансная частота отличается от частоты собственных колебании n0 =2 кГц с коэффициентом затухания 800 с-1.
ЗАДАНИЕ №4
|
|
|



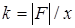 - коэффициент жёсткости пружины.
- коэффициент жёсткости пружины.