Молекулярная физика и термодинамика

Молекулярная физика и термодинамика

Таблица вариантов

Номера вариантов	Номера задач по порядку
		31
		34
		35
		36
		37
		38
		39
		41
12	12
15	15
16	16	46
		47
		49
		50
		51

 

Примеры решения задач

Пример №1. Найти среднюю кинетическую энергию одной молекулы аммиака NH₃ при температуре 27 °С.

Решение. Средняя полная энергия молекулы определяется по формуле:

,

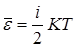где i – число степеней свободы молекулы, К – постоянная Больцмана,      Т – термодинамическая температура.

Число степеней свободы i для четырехатомной молекулы равно 6, три степени свободы приходится на поступательное движение молекулы, а три – на вращательное движение.

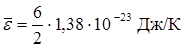(27+273)К = 1, 24× 10^-20 Дж

 

Пример №2 . Дана смесь газов, состоящая из азота и кислорода. Масса азота 8 кг, масса кислорода 2 кг. Газы считать идеальными. Определить удельные теплоемкости смеси газов с_р и с_v.

Решение. Удельные теплоёмкости идеальных газов в процессах р=соnst, v=соnst определяются формулами:

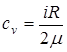
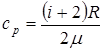
где i – число степеней свободы молекул газа, m – масса моля газа. Количество теплоты dQ, сообщенное смеси, равно

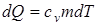
где m – масса смеси, т. к. имеется смесь газов, то

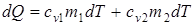
Сравнив две последние формулы, получим

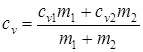
Аналогичное выражение получим для с_р

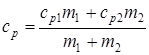
Из выше описанного следует:

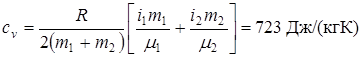
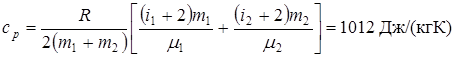
Пример №3 . Водород в количестве 0, 2 кг нагревается от температуры Т1=273К до температуры Т2=373К при постоянном давлении. Найти количество теплоты, поглощаемое газом, изменение его внутренней энергии и работу, совершаемую газом.

Решение. Количество теплоты, поглощаемое газом при изобарном нагревании определяется так:

Удельная теплоёмкость находится из выражения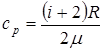

Подставим это выражение в соотношение для количества теплоты:

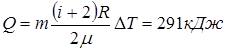
Изменение внутренней энергии газа:

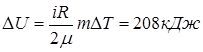
Работа, совершаемая газом, находится из первого закона термодинамики:

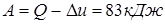
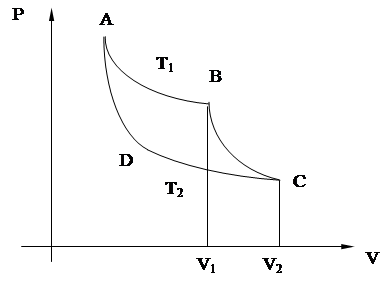
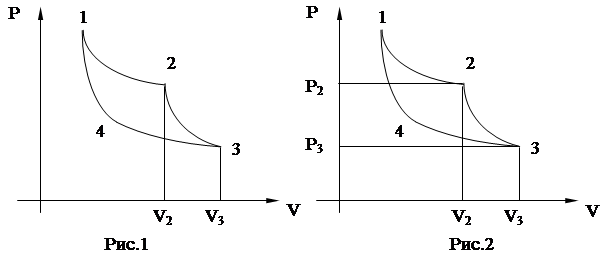
Пример №4 . Идеальный двухатомный газ совершает цикл Карно, график которого изображен на рис. 1. Объемы газов в состояниях В и С соответственно равны V1=12 л, V2=16 л. Найти КПД цикла Карно.

Решение. Количество теплоты, поглощаемое газом при изобарном нагревании определяется так:

 

 

КПД цикла Карно определяется так:

,

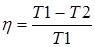Т1 и Т2 – температуры нагревателя и холодильника соответственно. При температурах Т1 и Т2 протекают изотермические процессы АВ и CD. Так как точки В и С лежат на одной адиабате ВС, то температуры в точках В и С можно связать уравнением Пуассона:

 

,

где .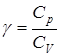

Из этих соотношений и выражения для КПД следует, что

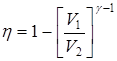 и

 

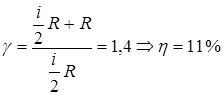
Пример №5. Тепловая машина Карно, имеющая КПД 40%, используется как холодильная машина. Найти величину холодильного коэффициента и количество теплоты, перенесенное от холодильника к нагревателю за один цикл, если известно, что совершаемая за цикл механическая работа 200Дж.

 

Решение. Холодильным коэффициентом называется отношение теплоты, отнятой у холодильника, к совершённой для этого работе:   

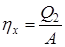
В тепловой машине Карно КПД определяется как 

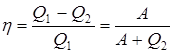
Так как машина обратима, то при обратном цикле она забирает от холодильника столько же теплоты Q₂, сколько передаёт при прямом цикле. То есть в верхних выражениях Q₂ одна и та же. С учётом. этого

Задачи для самостоятельного решения

2. Из баллона со сжатым газом вытекал газ. Какая часть газа осталась в баллоне, если первоначально при температуре 27°С манометр показывал    6 МПа, а через некоторое время при температуре 12°С показание манометра уменьшилось на 4 МПа?

2. Сколько молекул ртути содержится в 1м³ воздуха в помещении, зараженном ртутью, при температуре 20° С, если давление паров ртути при этой температуре равно 0, 645 Па? К=1, 38× 10^-23 Дж/К.

3. Цилиндрический сосуд делится подвижным поршнем на две части. Длина сосуда 85 см. В обе части сосуда помещены одинаковые массы кислорода и водорода. Какова длина отсека, занятого кислородом, при равновесном положении поршня? m₁ = 32× 10^-3 кг/моль; m₂ = 2× 10^-3 кг/моль.

4. Плотность газовой смеси водорода и кислорода равна 0, 48 кг/м3. Массовые доли газов равны соответственно 1/9 и 8/9. Давление смеси равно 100 кПа. Какова температура смеси? m₁ = 2× 10^-3 кг/моль; m₂ = 32× 10^-3 кг/моль.

5. В баллоне объемом 25 л находится водород при температуре 17°С. На сколько понизилось давление в баллоне после того, как было израсходовано  8, 3 г водорода? m₂ = 2× 10^-3 кг/моль.

6. Определить плотность водяного пара в воздухе при температуре 27°С, если давление пара при этой температуре равно 3, 55 кПа. m = 18× 10^-3 кг/моль

7. Открытый сосуд емкостью 0, 03 м³ нагревается от 20°С до 60°С. Какой объем воздуха выйдет при этом из сосуда?

8. Баллон объемом 0, 015 м³ содержит 7× 10^-3 кг азота и 4, 5× 10^-3 кг водорода при температуре 27°С. Определить давление смеси. m₁ = 28× 10^-3 кг/моль;         m₂ = 2× 10^-3 кг/моль.

9. При каком давлении средняя длина свободного пробега молекул азота равна 1 мм, если при нормальном давлении она равна 6× 10^-8 м? Рн=10⁵ Па.

10.  Давление газа вследствие сжатия увеличилось в 10 раз. Как изменилась длина свободного пробега молекул в газе, если процесс сжатия изотермический?

11. Средняя кинетическая энергия одной молекулы трехатомного газа равна 1, 2× 10^-20 Дж. Определить среднюю энергию вращательного движения этой молекулы при той же температуре.

12. Средняя кинетическая энергия одной молекулы двухатомного газа равна 1, 2× 10^-20 Дж. Определить среднюю энергию вращательного движения этой молекулы при той же температуре.

13. Определить среднюю кинетическую энергию одной молекулы четырехатомного газа при температуре 27°С. К=1, 38× 10^-23 Дж/К.

14. Средняя кинетическая энергия молекулы углекислого газа (СО₂) равна 1, 24× 10^-20 Дж. Какова температура газа. К=1, 38× 10^-23 Дж/К.

15. Давление газа 10^-3 Па, концентрация его молекул равна 10¹⁶ м^-3. Определить температуру газа и среднюю кинетическую энергию поступательного движения одной молекулы. К=1, 38× 10^-23 Дж/К.

16. Средняя кинетическая энергия поступательного движения молекулы газа равна 1, 5× 10^-19 Дж. Определить давление и температуру газа, если концентрация его молекул равна 10¹⁶ м^-3. К=1, 38× 10^-23 Дж/К.

17. Средняя кинетическая энергия вращательного движения трехатомной молекулы газа равна 3× 10^-19 Дж. Определить полную кинетическую энергию молекулы газа при той же температуре.

18. Средняя кинетическая энергия вращательного движения двухатомной молекулы газа равна 10^-19 Дж. Определить давление газа, если концентрация его молекул равна 10¹⁶ м^-3.

19. Среднее значение полной кинетической энергии одной молекулы водяного пара равно 1, 66× 10^-20 Дж. Определить температуру газа. К=1, 38× 10^-23 Дж/К.

20. Давление газа 10^-3 Па, концентрация его молекул равна 10¹⁶ м^-3. Определить среднюю кинетическую энергию вращательного движения молекулы, если она состоит из двух атомов.

21. Давление газа 10 Па, объем 10м³, средняя кинетическая энергия поступательного движения молекулы равна 1, 5× 10^-19 Дж. Сколько молекул газа содержится в этом объеме?

22. В баллоне вместимостью 2 м³ содержит газ при давлении 10^-3 Па. Общее число молекул газа составляет 2× 10¹⁶. Определить кинетическую энергию, приходящуюся в среднем на одну степень свободы молекулы.

23. Средняя кинетическая энергия поступательного движения молекулы газа составляет 1, 5× 10^-20 Дж, средняя кинетическая энергия вращательного движения той же молекулы  10^-20 Дж. Сколько атомов содержат молекулы газа?

24. Среднее значение полной кинетической энергии двухатомной молекулы газа равно 2, 5× 10^-20 Дж. Определить температуру газа. К=1, 38× 10^-23 Дж/К.

25. Средняя кинетическая энергия вращательного движения молекулы газа равна 0, 5× 10^-20 Дж. Какова полная кинетическая энергия молекулы газа, если газ двухатомный.

26. Какое количество водорода продиффундирует через площадку 2 м² за время 1 ч, если градиент плотности в направлении, перпендикулярном площадке, равен 10^-5 кг/м⁴. Коэффициент диффузии равен 3, 58× 10^-6 м²/с.

27. Пространство между двумя параллельными пластинами заполнено гелием. Расстояние между пластинами 50 мм. Одна пластина поддерживается при температуре 20 °С. другая – при температуре 40 °С. Коэффициент теплопроводности гелия равен 40 мВт/м× К. Вычислить плотность потока тепла между пластинами.

28. Между двумя параллельными пластинами находится воздух. Коэффициент теплопроводности воздуха 13× 10^-3 Вт/м× К Расстояние между пластинами 0. 1 см, площадь пластин 0, 2 м², разность температур пластин равна 100 К. какое количество тепла передается от пластины к пластине за 1 с?.

29. Вязкость воздуха при нормальных условиях равна 0, 18 мПа× с, плотность воздуха при этих условиях равна 1, 29 кг/м³. Определить коэффициент диффузии.

30. Давление газа равно 10⁴ Па, а средняя квадратичная скорость равна

500 м/с. Найти плотность этого газа.

31. Дана смесь газов, состоящая из неона, масса которого m₁= 4 кг, и водорода, масса которого m₂= 1 кг. Газы считать идеальными. Определить удельную теплоемкость смеси газов в процессе p = const. m₁ = 20× 10^-3 кг/моль;

m₂ = 2× 10^-3 кг/моль.

32. Дана смесь газов, состоящая из неона, масса которого m₁= 4 кг, и водорода, масса которого m₂= 1 кг. Газы считать идеальными. Определить удельную теплоемкость смеси газов в процессе v = const. m₁ = 20× 10^-3 кг/моль;

m₂ = 2× 10^-3 кг/моль.

33. Имеем некоторый идеальный двухатомный газ, разность его удельных теплоемкостей при постоянном давлении с_р и при постоянном объеме равна с_v равна 260 Дж/кгК. Определить массу киломоля газа и его удельную теплоемкость c_v.

34. Имеем некоторый идеальный газ /двухатомный/, разность его удельных теплоемкостей при постоянном давлении с_р и при постоянном объеме с_v=260Дж/кгК. Определить массу киломоля газа и его удельную теплоемкость с_р.

35. Определить удельную теплоемкость с_р смеси газов, содержащей 75% азота и 25% кислорода. m₁ = 28× 10^-3 кг/моль; m₂ = 32× 10^-3 кг/моль.

36. Определить удельную теплоемкость с_v смеси газов, содержащей 75%
азота и 25% кислорода. m₁ = 28× 10^-3 кг/моль; m₂ = 32× 10^-3 кг/моль.

37. Смесь газов состоит из 10 г гелия и 4 г водорода. Определить от-ношение Ср/Сv для данной смеси. m₁ = 4× 10^-3 кг/моль; m₂ = 2× 10^-3 кг/моль.

38. Смесь газов состоит из гелия и водорода, причем гелия содержится 10г. Отношение Ср/Сv для данной смеси равно 1, 52. Какое количество водорода содержится в смеси? m₁ = 4× 10^-3 кг/моль; m₂ = 2× 10^-3 кг/моль.

39. 25% молекул кислорода диссоциировали на атомы. Определить удельную теплоемкость с_р такого газа.  m = 32× 10^-3 кг/моль.

40.. 25% кислорода диссоциировали на атомы. Определить удельную теп­лоемкость c_v  такого газа. m = 32× 10^-3 кг/моль.

41. Определить молярную массу некоторого газа, если известно, что его удельные теплоемкости равны c_p= 0, 53× 10³ Дж/кг× К; c_v= 0, 32× 10³ Дж/кг× К.

42. Определить удельную теплоемкость с_р аргона, если известна его удельная теплоемкость c_v= 320 Дж/кг× К. m = 40× 10^-3 кг/моль.

43 Определить удельную теплоемкость c_v аргона, если известна его удельная теплоемкость c_р= 530 Дж/кг× К. m = 40× 10^-3 кг/моль.

44. Изохорная и изобарная удельные теплоемкости соответственно равны     

c_v = 3, 14× 10³ Дж/кг× К; c_р = 5, 22 Дж/кг× К. Найти молярную массу газа.

45. Какая часть молекул парообразного йода I₂. диссоциировала на атомы, если удельная теплоемкость c_р оказалась равной 140 Дж/кг× К? Масса одного моля йодаМ=253, 8× 10^-3 кг/моль.

46. Смесь газов состоит из хлора и криптона, взятых при одинаковых условиях и в равных объемах. Определить удельную теплоемкость с_р смеси.

m₁ = 70, 9× 10^-3 кг/моль; m₂ = 83, 8× 10^-3 кг/моль.

47. Найти показатель адиабаты g для смеси газов, содержащей гелий m₁=10 г и водорода массой m₂=4 г. m₁ = 4× 10^-3 кг/моль; m₂ = 2× 10^-3 кг/моль.

48. Смесь газов состоит из аргона и азота, взятых при одинаковых ус­ловиях и в одинаковых объемах. Определить показатель адиабаты такой смеси. m₁ = 40× 10^-3 кг/моль; m₂ = 28× 10^-3 кг/моль.

49. Определить показатель адиабаты g частично диссоциированного газообразного азота, степень диссоциации которого равна 0, 4. m = 28× 10^-3 кг/моль.

50. Определить степень диссоциации газообразного хлора, если показатель адиабаты у такого газа равен 1, 55. m = 70, 9× 10^-3 кг/моль.

51. Степень диссоциации газообразного хлора равна 0, 517. Найти показатель адиабаты такого частично диссоциированного газа. m = 70, 9× 10^-3 кг/моль.

52. Показатель адиабаты частично диссоциированного газообразного азота равен 1, 52. Найти степень диссоциации такого газа. m = 28× 10^-3 кг/моль.

53. Определить удельную теплоемкость c_v смеси газов, содержащую V₁=5л водорода и V₂= 3 л гелия. Газы находятся при одинаковых условиях.

m₁ = 2× 10^-3 кг/моль.

54. Удельные теплоемкости водорода и неона при постоянном объеме соответственно равны с_v1 = 10, 4 кДж/кг× К, с_v2 = 0, 624 кДж/кг× К. Вычислить удельную теплоемкость с_v смеси водорода и неона. Массовые доли газов соответственно равны w₁=0, 2, w₂=0, 8. m₁ = 2× 10^-3 кг/моль; m₂ = 20× 10^-3 кг/моль.

55. Найти показатель адиабаты смеси водорода и неона, если массовые доли газов в смеси одинаковы и равны 0, 5. m₁ = 2× 10^-3 кг/моль; m₂ = 20× 10^-3 кг/моль.

56. Определить молярную массу и число степеней свободы молекулы некоторого газа, если известно, что его удельные теплоемкости равны

c_v = 0, 624 Дж/кг× К; c_р = 1, 04 Дж/кг× К.

57. Определить молярную массу и число степеней свободы молекулы некоторого газа, если известно, что его удельные теплоемкости равны

c_v = 10, 4 Дж/кг× К; c_р = 14, 6 Дж/кг× К.

58. Найти отношение Ср/Сv азота (N₂).

59. Найти число степеней свободы молекулы газа, если показатель адиабаты для этого газа равен 1, 4.

60. Найти показатель адиабаты для воздуха.

61. Один моль гелия изобарически расширяется от объема V₁= 5л до объема

V₂= 1 0 л при давлении р = 2026 гПа, Сv = 1 2, 25 Дж/моль× К. Определить изменение внутренней энергии газа в этом процессе, считая его идеальным.

R=8, 31Дж/моль× К.

62. Один грамм кислорода нагревается от t1=10°С до t2 =60°C при р = const Определить изменение внутренней энергии газа, газ идеальный. m = 32× 10^-3 кг/моль

63. Один грамм кислорода нагревается от t1=10°С до t2 =60°C при v = const Определить изменение внутренней энергии кислорода, считая его идеальным..

m = 32× 10^-3 кг/моль

64. Один грамм кислорода нагревается от t1=10°С до t2 =60°C при dQ = 0. Определить изменение внутренней энергии газа, газ идеальный. m = 32× 10^-3 кг/моль

65. Атмосферный воздух в объеме 10 л подвергается 12-кратному сжатию Начальное давление р₁= 10⁵ Па. Начальная температура 10°С. Процесс сжатия адиабатический. Определить конечное давление.

66. Воздух в объеме 10 л подвергается 12-кратному сжатию. Начальное

давление р₁= 10⁵ Па. Начальная температура 10°С. Процесс адиабатический. Определить конечную температуру.

67. Воздух в объеме 10 л подвергается 12-кратному сжатию. Начальное

давление р₁= 10⁵ Па. Начальная температура 10°С. Процесс адиабатический, газ идеальный. Определить работу сжатия.

68. 12л азота расширяются при постоянном давлении р = 10⁵ Па до объема 22 л. Газ идеальный. Найти изменение внутренней энергии газа. m = 28× 10^-3 кг/моль

69. 200 г азота нагреваются при постоянном давлении от 20°С до 100°С. Газ идеальный. Определить прирост внутренней энергии газа. m = 28× 10^-3 кг/моль

70. 3л воздуха под давлением р=10⁵ Па изотермически сжимают до объема 0, 5 л. Определить количество тепла, выделившееся при этом сжатии.

m = 29× 10^-3 кг/моль

71. Один моль газа при постоянном давлении р=10⁵ Па сжимают, при этом его температура изменяется от t1=20°С до t2=5°С. Газ считать идеальным. Определить работу сжатия газа.

72. 2 л азота при давлении р=10⁵ Па и температуре Т=27°С расширяются адиабатически до объема V=40л. Газ считать идеальным. Определить давление после расширения и работу расширения газа. m = 28× 10^-3 кг/моль

73. 2 л азота при давлении р=10⁵ Па и температуре Т=27°С расширяются адиабатически до объема V=40л. Газ считать идеальным. Определить температуру после расширения и работу расширения газа. m = 28× 10^-3 кг/моль

74. Один моль кислорода, находясь при температуре 27°С, при изотермическом расширении поглотил 100 Дж. Во сколько раз увеличился его
объем?

75. Один моль кислорода, находясь при температуре 27°С. при изо­терми-ческом расширении увеличил объем в 2 раза. Сколько тепла поглотил газ?

76. 160 г кислорода было нагрето на 12°С. При этом было затрачено 1750Дж теплоты. Определить, как протекал процесс нагревания при r=const или v=const

m = 32× 10^-3 кг/моль

77. 160 г кислорода было нагрето на 12°С при постоянном давлении. Определить количество теплоты, затраченное на нагревание. m = 32× 10^-3 кг/моль

78. Баллон содержит 220 г углекислого газа под давлением 9× 10⁵ Па и температуре 15°С. Вследствие охлаждения давление упало до 8× 10⁵ Па. Определить количество теплоты, отданное газом. m = 44× 10^-3 кг/моль

79. Объем газа при адиабатическом сжатии уменьшился в 10 раз, а давление увеличилось в 21, 4 раза. Определить отношение удельных теплоемкостей газа

80. 12 л азота расширяется при постоянном давлении до объема 22л. Изменение внутренней энергии равно 2, 5 • 10³ Дж. Каково давление газа?

m = 28× 10^-3 кг/моль

81. 1 м³ водорода при 0°С находится в цилиндрическом сосуде, закрытом сверху легко скользящим, невесомым поршнем. Атмосферное давление равно 0, 96× 10⁵ Па. Определить количество теплоты, необходимое для нагревания водорода до 300°С? m = 2× 10^-3 кг/моль

82. Из баллона, содержащего водород под давлением р=10⁶ Па при тем­пературе 18°С, выпустили половину находившегося в нем количества газа. Процесс считать адиабатным. Определить конечную температуру и давление.

83. Смесь газов, состоящую из водорода m1= 4 г и кислорода m2 = 32 г удельные теплоемкости которых соответственно с_р1=14, З КДж/кгК. и

с_р2 =0, 9 КДж/кгК, охладили на Dt =20° С при постоянномобъеме. Для обоих газов g=1, 4. Определить потерю тепла при охлаждении этой системы.

84. Какое количество теплоты отдает один моль идеального одноатомного газа при изобарическом охлаждении от Т1 до Т2, если на его сжатие в ходе процесса затрачивается работа 8, 3 Дж. Удельная теплоемкость с_р=21 КДж/кгК

85. В сосуде объема 10 литров. находится кислород под давлением р= 10⁵ Па. Стенки сосуда могут выдержать внутреннее давление до р=10⁶Па. Cp/Cv=1, 4. Какое максимальное количество теплоты можно сообщить газу в  этом сосуде? m = 32× 10^-3 кг/моль

86. Смесь равных количеств /по массе/ водорода и гелия при 0°С помещена в цилиндрический сосуд объемом 1 м³, закрытый сверху невесомым поршнем. Атмосферное давление 970 гПа. Какое количество тепла требуется для нагревания смеси до 200°С? m₁ = 2× 10^-3 кг/моль; m₂ = 4× 10^-3 кг/моль.

87. Один моль идеального одноатомного газа, находящийся при темпе­ратуре 27°С, нагревают при постоянном давлении, затратив энергию 30 кДж. Определить работу расширения газа..

88. Один моль идеального газа /одноатомного/, находящийся при тем­пературе 27°С нагревают при постоянном давлении, затратив энергию    30 кДж. Найти изменение его внутренней энергии.

89. Расширяясь, водород совершил работу 6 кДж. Определить количество теплоты подведенной к газу, если процесс притекал изобарно.

90. Расширяясь, водород совершил работу 6 кДж. Определить количество теплоты, подведенное к газу, если процесс протекал изотермически.

91. Расширяясь, водород совершил работу А =6 кДж. Определить количество теплоты, подведенное к газу, если процесс протекал: 1/ изобарно; 2/ изотермически.

92. Гелий, расширяясь совершил работу 10 кДж. Определить количество
теплоты, подведенное к газу, если процесс протекал: 1/ изобарно; 2/ изотермически..

93. Углекислый газ при нагревании совершил работу 5 кДж. Определит количество теплоты, подведенное к газу, если процесс протекал: 1) изобарно;
2) изотермически

94. Расширяясь, кислород изменил свою внутреннюю энергию на 15 кДж. Определить совершенную им работу и количество теплоты, подведенной к газу, если процесс протекал изобарно.

95. Расширяясь, гелий изменил внутреннюю энергию на 9 кДж. Определить совершенную им работу и количество теплоты подведенной к газу, если
процесс протекал изобарно.

96. Углекислый газ при нагревании изменил внутреннюю энергию на 6 кДж Определить совершенную им работу и количество теплоты полу­ченное газом, если процесс протекал изобарно.

97. При изобарном нагревании водород получил 21 кДж теплоты. Оп­ределить совершенную им работу и изменение внутренней энергии газа.

98. При изобарном нагревании гелий получил количество теплоты 25 кДж. Оп­ределить совершенную им работу и изменение внутренней энергии газа.

99. При изобарном нагревании углекислого газа им было получено количество теплоты, равное 20 кДж. Какую работу совершил газ и на сколько изменилась его внутренняя энергия?

100. Расширяясь, кислород получил количество теплоты, равное 21 кДж. Какую работу совершил газ, расширяясь: 1/изобарно; 2/ изотермически.

101. Водяной пар расширяется, получив количество теплоты 4 кДж. Определить работу расширения и изменение внутренней энергии газа, если процесс протекал: I) изобарно; 2) изотермически.

102. Газ расширяется, получив количество теплоты 4 кДж. Работа расширения равна: I) 1 кДж; 2) 4 кДж. Какие процессы протекали в газе в первом и во втором случаях? Найти число степеней свободы молекул газа.

103. Расширяясь, газ совершил работу А = 6 кДж. получив количество теплоты: 1)21 кДж; 2) 6 кДж. Какие процессы протекали в газе в первом и во втором случаях.? Каким числом степеней свободы обладают молекулы газа?

104. Газ, расширяясь изобарно, совершил работу 10 кДж, получив количество теплоты 25 кДж Найти изменение внутренней энергии газа и число степеней свободы его молекул.

105. Расширяясь изобарно, газ изменил свою внутреннюю энергию на 15кДж, совершив. работу 6 кДж. Какое количество теплоты получил газ и каково число степеней свободы его молекул?

106. Газ, расширяясь изобарно, изменил внутреннюю энергию на 9 кДж, совершив работу 6 кДж. Какое количество теплоты получил газ и сколькими степенями свободы обладают его молекулы?

107. Газ при изобарном нагревании изменил внутреннюю энергию на      6 кДж, совершив работу 2 кДж. Какое количество теплоты получил газ и сколько степеней свободы имеют молекулы этого газа?

108. Водяной пар, расширяясь, получил количество теплоты 4 кДж. совершив при этом работу 1 кДж в первом случае и 4 кДж во втором. Какие процессы протекали в первом и во втором случаях. Найти изменение внутренней энергии пара в этих случаях.

109. Расширяясь изобарно, газ совершил работу 6 кДж, изменив внут­реннюю энергию на 15 кДж. Сколько атомов содержит молекула газа? Какое количество теплоты получил газ?

110. Газ, расширяясь изобарно, совершил работу 10 кДж, изменив внутреннюю энергию на 15 кДж. Какое количество теплоты получил газ? Сколько атомов содержится в его молекуле?

111. Газ, объемом 1 м³ сначала нагрели при постоянном давлении 

Р= 200кПа, а затем при постоянном объеме V= 3 м³. Общее количество тепла, сообщенное газу, равно 3, 65 МДж. Найти изменение внутренней энергии газа.

112. Газ объемом 1 м^З сначала нагрели при постоянном давлении         Р=200 кПа, а затем при постоянном объеме V=3 м³. Внутренняя энергия газа при этом изменилась на 3, 25 МДж. Какое количество тепла передано газу?

113. Газ сначала нагрели при постоянном давлении Р=200 кПа и затем при постоянном объеме, сообщив ему количество тепла 3, 65 МДж. Внутренняя энергия газа изменилась на 3, 25 МДж. На сколько изменился объем газа?

. 114.  Газ сначала нагрели изобарно, изменив его объем на 2 м³, а затем изохорно. Общее количество тепла, сообщенное газу, равно 3, 65 кДж. внутренняя энергия газа при атом изменилась на 3, 25 кДж. При каком давлении шло изобарное нагревание газа?

115. При адиабатном сжатии одного моля кислорода, его температура повысилась на 1000° С. Найти изменение внутренней энергии и работу сжатия газа.       

116. При адиабатном сжатии 1 моля углекислого газа температура его повысилась на 1000°С. Найти изменение внутренней энергии и работу сжа­тия газа.

117 При адиабатном сжатии 1 моля гелия его температура повысилась на 1000° С. Найти изменение внутренней энергии и работу сжатия газа.

118 При изотермическом расширении 1 моля водорода при температуре 300°К объем газа увеличился в 2, 7 раза. Определить работу расширения и количество тепла, полученного газом.

119 При изотермическом расширении 1 моля азота при температуре 500°К его объем увеличился в 2, 7 раза. Определить количество теплоты, полученное газом, и работу расширения газа.

120. При изохорном нагревании азота объемом 1 литр давление увели­чилось на 1 МПа. Определить количество теплоты, полученное газом, из­менение его внутренней энергии и работу газа.

121. Идеальный двухатомный газ совершает цикл Карно, график которого изображен на рисунке 1. Объемы газов в состояниях 2 и 3 соответственно равны 24 л и 32 л. Найти термический КПД цикла.

122. Идеальный трехатомный газ совершает цикл Карно, график которого изображен на рисунке 1. Объемы газов в состояниях 2, 3 соответственно равны 6 л и 8 л. Найти термический КПД цикла.

123. Идеальный одноатомный газ совершает цикл Карно, график которого изображен на рисунке 1. Объемы газов в состояниях 2, 3 соответственно равны 3 л и 4 л. Найти КПД цикла..

 

124. Идеальный двухатомный газ совершает цикл Карно, график которого изображен на рисунке 2. Давления газа в состояниях 2, 3 соответственно равны    5 × 10⁵ Па и 1 × 10⁵ Па. Найти КПД цикла..

125. Идеальный трехатомный газ совершает цикл Карно, график которого изображен на рис. 2. Давления газа в состояниях 2, 3 соответственно равны 600 кПа и 100 кПа. Найти КПД цикла.

126. Идеальный одноатомный газ совершает цикл Карно, график которого изображен на рис. 2. Давления газа в состояниях 2, 3 соответственно равны 400 кПа и 100 кПа. Определить КПД цикла..

127. Идеальный газ совершает цикл Карно, график которого изображен на рис. 2 Температуры газа в состояниях 1 и 3 соответственно равны t₁= 327°С и t₃= 127°С. Найти КПД цикла..

128. Идеальный газ совершает цикл Карно, график которого изображен на рис. 2. Температуры газа в состояниях 2 и 3 соответственно равны t₂ = 327° С и t₃ = 27 °С. Найти КПД цикла..

129. Идеальный газ, совершает цикл Карно, график которого изображен на рис. 2. Температуры газа в состояниях 1, 4 соответственно равны t₁ = 127° С и t₄ = 27 °С. Определить КПД цикла.

130. Идеальный газ совершает цикл Карно /рис. 2/; отношение температур в состояниях 1 и 3 Т₁/Т₃ равно 2. Найти КПД цикла.

Pmax, Vmin

131. Идеальный газ совершает цикл Карно, изображенный на рис. 3. Наименьший объем Vmin= 30 л, наибольший Vmax =50 л, наименьшее давление Рmin = 2 кПа, наибольшее Рmах=5 кПа. Найти КПД цикла.

 

	P
									Рис. 3

 

 

V

  

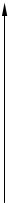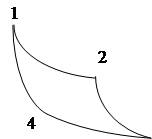
132. Идеальный газ совершает цикл Карно, изображенный на рис. 3. Мак­симальное давление газа в 2 раза больше минимального, а максимальный объем в 1, 5 раза больше минимального. Найти КПД цикла.

133. Идеальный газ совершает цикл Карно, изображенный на рис. 3, давления и объемы газа в состояниях 2, 3 соответственно равны Р₂= 400кПа, V₂=10л, Р₃= 200 кПа, V₃=15л. Найти КПД цикла.

134. Идеальный газ совершает цикл Карно, изображенный на рис. 3. При изотермическом расширении газ совершает работу 100 Дж, а при изотермическом сжатии 60 Дж. Каков КПД цикла.

 

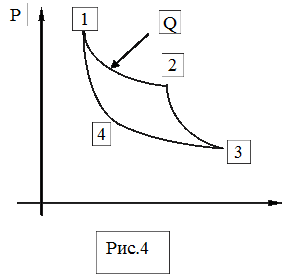135. Идеальный газ совершает цикл Карно, изображенный на рис. 4. В процессе 1-2 он получил количество теп-лоты Q = 100 Дж. Определить     работу газа за цикл, если температуры газа в состояниях 2 и 3 соответственно равны Т₂= 400 К, Т₃ = 300 К.

136. Идеальный газ совершает цикл Карно, изображенный на рис. 4.                В процессе 1-2 совершенная им работа равна 200 Дж. Определить работу газа за цикл, если температуры газов в состояниях 1 и 4 соответственно равны Т₁= 400 К и Т₄ =300 К.

137. Совершенная газом работа за 1 цикл Карно /рис. 4/ равна 50Дж. Температуры газа в состояниях 1 и 4 соответственно равны Т₁= 400 К и Т₄=300 К. Определить количество теплоты, полученное газом в процессе 1-2.

138. Совершенная газом работа за один цикл Карно /рис. 4/ равна 100 Дж, а работа в процессе 3-4 200 Дж. Каков КПД цикла.

139. Совершенная газом работа за один цикл Карно /рис. 4/ равна 100 Дж. Температуры газа в состояниях 1 и 3 соответственно равны Т₁= 400 К и Т₃=300 К. Какое количество тепла отдано холодильнику?

140. Идеальный газ совершает цикл Карно /рис. 4/. Каковы температуры газа в состояниях 1 и 4, если КПД цикла 0, 4, а температура в состоянии 3 составляет Т₃ = 600 К.

141. Тепловая машина работает по циклу Карно, КПД которого 0, 25. Каков будет холодильный коэффициент машины, если она будет совершать тот же цикл в обратном направлении.

142. Тепловая машина работает по циклу Карно, КПД которого 20%. Найти холодильный коэффициент машины, если она будет совершать тот же цикл в обратном направлении.

143. Холодильный коэффициент машины, совершающей обратный цикл Карно, 300 %. Найти КПД тепловой машины, работающей по тому же циклу Карно.

144. Холодильный коэффициент машины, совершающей обратный цикл Карно, 400%. Найти КПД тепловой машины, работающий по тому же циклу Карно.

145. Идеальный газ совершает цикл Карно /рис. 4/. Температуры газов в состояниях 2 и 3 соответственно равны 500 К и 300 К. Работа, совершаемая за один цикл, равна 100 кДж. Определить количество теплоты, переданное газом холодильнику.

146. Идеальный двухатомный газ совершает цикл Карно. В процессе адиабатного расширения его объем увеличива

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: