Раздел 2. Средняя длина свободного пробега молекул газа. Явления переноса.

АЛАДиНСКАЯ Л. И.

 

РЕШЕНИЕ ЗАДАЧ

ПО МОЛЕКУЛЯРНОЙ ФИЗИКЕ

И ТЕРМОДИНАМИКЕ

 

Учебно-методическое пособие

для студентов 2 курса

специальности 080801

«Прикладная информатика в экономике»

 

 

Москва 2015

 

УДК 004.89

ББК 32.813

 

Решение задач по молекулярной физике и темодинамике. Учебно-методическое пособие/ Аладинская Л.И. – М.: МГУПИ, 2015. - 85 с.

 

Предлагаемое издание рекомендуется в качестве учебно-методического пособия для подготовки студентов 2 курса по дисциплине «Физика» специальности 080801 «Прикладная информатика». В пособии представлены примеры решения задач по основным вопросам курса физики 4-го семестра, а именно по молекулярной физике и термодинамике. Помимо этого в пособии рассмотрены задачи по физике атомного ядра.

Материал пособия изложен в соответствии с государственным стандартом по указанной специальности. Пособие может быть полезно для самостоятельной работы студентов при подготовке к контрольным работам и экзаменам.

Рецензенты:

 

 

Учебно-методическое пособие рассмотрено и одобрено на заседании кафедры ЭФ-2, протокол №.

 

 

ã Каф. ЭФ-2. МГУПИ, 2015 г.

ã Компьютерная верстка Аладинская Л.И.., 2015 г.

Раздел 1. Молекулярная физика. Основное уравнение молекулярно-кинетической теории идеального газа.

Пример 1.1. Сколько молекул содержится в V=1 см³ воды? Какова масса молекулы воды? Молярная масса μ=0,018 .

Решение. Число частиц N в данном количестве вещества ν находится по формуле N=νN_А= N_А, где N_А – число Авогадро. Поскольку m=ρV, где ρ – плотность воды, получим: N= N_А. Поскольку в 1 моле вещества содержится N_А молекул, масса одной молекулы m₀= . Подставив числовые данные, получим: N=3,33·10²², m=2,99·10^{-26 кг.}

 

Пример 1.2. Оценить размер атома золота. Плотность золота ρ=19,32·10³ , молярная масса μ=0,197 .

Решение. Масса m вещества, содержащая N атомов: m=ρNV₀ (1), где V₀ –объём, занимаемый одним атомом. Поскольку масса атома m₀= , для массы вещества получим: m=Nm₀= 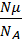(2). Приравнивая правые части (1) и (2), получим: V₀ = . На каждый атом приходится куб со стороной L ~ . В твёрдых телах атомы упакованы плотно, поэтому величина L близка к размеру атома. Подставляя числовые данные, получим: L=0,26·10^{-9 м = 0,26 нм.}

 

Пример 1.3. В результате нагревания давление газа в закрытом сосуде увеличилось в N раз. Во сколько раз увеличилась средняя квадратичная скорость его молекул?

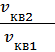Решение. Давления газа до и после нагревания соответственно определяются формулами p₁=⅓m₀nv_кв1² и p₂=⅓m₀nv_кв2². Отметим, что при нагревании в закрытом сосуде концентрация молекул n не меняется. Разделив эти уравнения друг на друга, получим: = или =N^½.

 

Пример 1.4. Давление газа p=100 кПа, средняя квадратичная скорость его молекул v_кв = 400 . Найти плотность газа.

Решение. Поскольку плотность может быть выражена как произведение массы молекулы на число молекул в единице объёма (концентрацию), основное уравнение МКТ можно записать в виде p=⅓m₀nv_кв² =⅓ρv_кв². Выразив отсюда плотность, получим ρ = .

 

 

Пример 1.5. Найти число молекул газа N, если средняя квадратичная скорость этих молекул v_кв = 500 , масса газа m=0,01 кг, а температура t=27ºC.

Решение. Число молекул можно найти по формуле

 

N=νN_А=()N_А.

 

Молярную массу выразим из формулы для средней квадратичной скорости

 

v_кв = (.

Отсюда

μ= .

 

Подставив это в формулу для N, получим:

N=mv_кв² 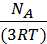или N = .

 

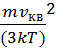Здесь k –постоянная Больцмана, Т – абсолютная температура газа, Т=27+273 =300 К. После расчётов получим: N=2·10²³.

 

 

Раздел 2. Средняя длина свободного пробега молекул газа. Явления переноса.

 

Пример 2.1. Средняя длина свободного пробега молекулы углекислого газа при нормальных условиях равна 4·10^-6 см. Какова средняя арифметическая скорость молекул? Сколько столкновений в секунду испытывает молекула?

Решение. Средняя арифметическая скорость молекул находится по формуле ū= 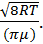Нормальные условия – это температура 273 К и давление 100 кПа. Подставив числовые значения, получим ū=362 .

Среднее число столкновений молекулы в секунду ž зависит от средней формулой . После подстановки данных и расчёта получим: = 9,05·10⁹ с^-1.

 

 

Пример 2.2. При каком давлении средняя длина свободного пробега молекул водорода равна 2,5 см, если температура газа 67°C? Диаметр молекулы считать равным 0,28 нм.

Решение. Давление газа можно найти по формуле p=nkT, где n- концентрация газа, k –постоянная Больцмана, Т – абсолютная температура, равная по условию 340 К. Концентрацию газа выразим из формулы для средней длины свободного пробега. Получим: n . Подставив это в формулу давления, получим: . После подстановки числовых данных и расчёта получим: p = 0,539 Па.

 

 

Пример 2.3. Найти коэффициент теплопроводности азота, имеющего температуру 280 К. Эффективный диаметр молекулы азота считать равным 0,38 нм.

Решение. Коэффициент теплопроводности λ газа рассчитывается по формуле λ=⅓c_Vρ ū, где c_V - удельная теплоёмкость газа при постоянном объёме, ρ – плотность газа, – средняя длина свободного пробега молекул, ū – средняя арифметическая скорость молекул. Величину c_V можно найти по формуле c_V = 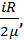где i=5 – число степеней свободы молекул азота (двухатомная молекула), μ – молярная масса газа, R – универсальная газовая постоянная.

Плотность газа можно найти, воспользовавшись уравнением состояния идеального газа pV= RT. Учитывая, что плотность ρ= , из уравнения состояния получим: ρ= . Давление нам неизвестно, однако, в соответствии с формулой p=nkT, оно прямо пропорционально концентрации n, входящей в выражение для средней длины свободного пробега =(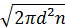)^-1. В связи с этим концентрация n сократится при подстановке выражений для p и в формулу для λ. Подставив туда эти выражения, а также формулу для средней арифметической скорости, после упрощения можно получить: λ=i k(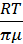)^½ /(3πd²). После подстановки числовых данных и расчётов получим:

λ=8,25 .

 

 

Пример 2.4. Наружная поверхность неоштукатуренной кирпичной стены толщиной Δx= 50 см (два кирпича) имеет температуру -10 ºC, внутренняя +20ºC. За сутки через 1 м² стены за счёт теплопроводности теряется количество тепла Q=3,6 ·10⁶ Дж. Определить коэффициент теплопроводности кирпичной кладки.

Решение. Будем считать стену бесконечной, температуры Т₁ и Т₂ постоянными, а процесс теплопроводности установившимся. Тогда уравнение теплопроводности можно записать в виде: Q=λSt·(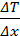), где Q – количество теплоты, прошедшей через стену толщиной Δx при разности температур ΔT= Т₂ – Т₁ через площадь S за время t, λ – коэффициент теплопроводности. Тогда λ можно выразить следующим образом:

 

λ=Q· .

 

После подстановки числовых данных и последующего расчёта получим: λ=0,69 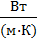. Сравнивая с результатом предыдущей задачи, можно отметить, что коэффициент теплопроводности твёрдого тела на два порядка превышает этот коэффициент для газа при сравнимых температурах.

 

 

Пример 2.5. Определить массу азота, прошедшего вследствие диффузии через площадку S=50 см² за время t=20 с, если градиент плотности в направлении, перпендикулярном площадке, 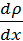=1 . Температура азота T=290 К, а средняя длина свободного пробега его молекул равна =1 мкм.

Решение. Запишем закон Фика (без учёта знака) для массы вещества, прошедшего вследствие диффузии через площадку S за время t при градиенте плотности 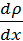: m=D(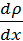)St.

Коэффициент диффузии находится по формуле D=⅓ū , где ū – средняя арифметическая скорость молекул, – средняя длина свободного пробега молекул. Как известно, средняя арифметическая скорость находится по формуле ū=[ 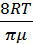]^½. Подставив эту формулу и остальные данные задачи в закон Фика, после расчётов получим: m=15,6 мг.

 

 

12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: