Раздел 5. Круговые процессы (циклы) и их КПД . Тепловые машины.

 

 

Пример 5.1.

 

Один моль (ν=1 моль) идеального двухатомного газа, занимающий объём 12,3 л под давлением 200 кПа, нагревается при постоянном объёме до давления 300 кПа. Далее газ расширяется при постоянном давлении до объёма 24,6 л, после чего охлаждается при постоянном объёме до начального давления и, наконец, сжимается при постоянном давлении до начального объёма. Определить: 1) температуры газа для характерных («поворотных») точек цикла; 2) термический КПД цикла.

Решение. Из условия задачи следует, что цикл состоит из двух изохорических и двух изобарических процессов. Введём обозначения. Наименьший объём газа - V', наибольший -V", наименьшее давление - p', наибольшее - p". Начальная и конечная температура газа – Т₁, температура после изохорического нагревания – Т₂, после изобарического расширения – Т₃, после изохорического охлаждения – Т₄.

Температуру в начальном состоянии определим из уравнения Клапейрона-Менделеева p'V'=νRT₁. Отсюда Т₁ = Сделав подстановку числовых значений, получим Т₁ =290 К.

При изохорическом процессе давление газа прямо пропорционально абсолютной температуре: p"/p'= , откуда T₂ =T₁ = 435 К.

При изобарическом процессе объём газа прямо пропорционален абсолютной температуре: 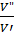= , откуда T₃=Т₂ 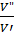= 870 К.

Точно так же, для последнего, изобарического этапа цикла = , откуда T₄ =Т₁ =580 К. Характерные температуры найдены.

Термический КПД любого цикла определяется формулой

η= 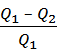= 1 - ,

где Q₁ – теплота, полученная газом за один цикл от нагревателя, Q₂ – теплота, отданная за один цикл охладителю, Q₁ – Q₂ - теплота, превращаемая в механическую энергию.

Теплота, полученная газом при изохорическом нагревании (первый этап цикла), Q_1-2 =νC _V(T₂ –T₁).

Теплота, полученная при изобарическом расширении (второй этап цикла),

Q_2-3 =νC _р(T₃ –T₂).

 

Газ принимает теплоту от нагревателя именно на первых двух этапах цикла. Полная теплота, полученная газом от нагревателя,

Q₁= Q_1-2 + Q_2-3 = νC _V(T₂ –T₁)+ νC _р(T₃ –T₂).

 

Таким же образом найдём полную теплоту, отданную газом охладителю при изохорическом охлаждении (третий этап цикла) и изобарическом сжатии (четвёртый этап):

Q₂= Q_1-2 + Q_2-3 = νC _V(T₃ –T₄)+ νC _р(T₄ –T₁).

 

Подставив формулы для Q₁ и Q₂ в выражение для термического КПД, после числовых расчётов получим η = 1 – 0,923 = 0,077 = 7,7 %.

 

Пример 5.2. Трёхатомный газ (i=6) газ совершает цикл Карно. Объём газа после изотермического расширения составляет V₁ = 6 м³. Определить объём газа после адиабатического расширения, если КПД цикла η=22 %.

Решение. Обозначим температуры газа в начале и в конце адиабатического расширения Т₁ и Т₂. Запишем уравнение Пуассона для адиабатического процесса в виде: 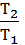= ()^γ-1, где γ= = - показатель адиабаты. Нетрудно рассчитать, что для трёхатомного газа γ-1=⅓. Тогда уравнение Пуассона запишется в виде:

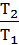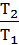= ()^⅓ → = ()³.

Отношение находим из формулы для КПД цикла Карно:

η = 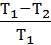=1 - → 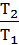= 1 – η.

 

Тогда отношение объёмов выразится формулой: = (1 – η)³.

Выражая отсюда конечный объём, получим: V₂ = .

Произведя вычисления, найдём: V₂ = 12,6 м³.

 

Пример 5.3. Температура нагревателя идеальной тепловой машины t₁ =117°C, а холодильника t=27°C. Количество теплоты, получаемое машиной от нагревателя за t = 1с, равно Q₁ =60 кДж. Найти количество теплоты Q₂, отдаваемое холодильнику за это время, и мощность машины N.

Решение. КПД идеальной тепловой машины можно выразить через принимаемую и отдаваемую теплоту или через температуры нагревателя и холодильника. Приравняв эти выражения, получим: , или 1- =1 - . Из выражения = можно получить Q₂ =Q₁ .

Мощность тепловой машины равна её работе в единицу времени: N= . Работа А равна разности между количеством теплоты Q₁, полученным рабочим телом от нагревателя, и количеством теплоты Q₂, отданным им холодильнику. Таким образом, мощность N= .

Переведя данные в единицы СИ и произведя вычисления, получим: Q₂ =46 кДж, N=14 кВт.

 

 

Пример 5.4. Нагреватель тепловой машины, работающей по циклу Карно, имеет температуру t₁ = 200 °C (Т₁=473 К). Какова температура холодильника, если за счёт каждой килокалории тепла, полученной от нагревателя, машина совершает работу 1,68 кДж?

Решение. Температуру охладителя можно найти из выражения для КПД машины, работающей по циклу Карно: η= , где Т₁ и Т₂ - абсолютные температуры нагревателя и холодильника. Отсюда Т₂ = Т₁ (1 – η).

Термический КПД тепловой машины есть коэффициент использования теплоты. Он выражает отношение теплоты, которая превращается в механическую работу А, к теплоте Q₁, которая получена рабочим телом от нагревателя, т.е.η= . С учётом этой формулы Т₂ = Т₁ (1 – ). Подставив сюда числовые значения, получим Т₂ =284 К.

 

 

Раздел 6. Энтропия.

 

Пример 6.1. Найти изменение энтропии при охлаждении азота массой m=10 г от 80°C до 0°C при постоянном объёме и при постоянном давлении.

Решение. Как известно, изменение энтропии можно найти по формуле:

ΔS=S₂ –S₁ , где dQ – малое изменение энтропии при температуре Т.

 

При изохорическом процессе dQ_V =mC_V =

 

При изобарическом процессе dQ_р=mC_р = .

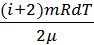Подставляя эти формулы в выражение для ΔS и проводя интегрирование, получим:

–для изохорического процесса,

 

 

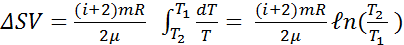– для изобарического процессa.

Произведя вычисления по этим формулам, получим: ΔS_V = -1,93 ;ΔS_р = -2,7 .

Пример 6.2. Найти изменение энтропии при изотермическом расширении 6 г водорода, если его начальное давление 100 кПа, а конечное 50 кПа.

Решение. Известно, что изменение энтропии выражается формулой:

, где dQ – малое изменение энтропии при температуре Т.

Из первого начала термодинамики следует, что dQ= C_V dT+pdV. Здесь С_V – молярная теплоёмкость газа при постоянном объёме (далее С_р – молярная теплоёмкость при постоянном давлении). Разделим обе части этого равенства на Т и учтём, что из уравнения Клапейрона-Менделеева следует: = . Тогда будем иметь следующее выражение:

 

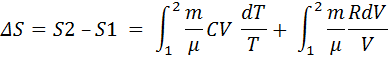
Проведя интегрирование, получим: ΔS= C_V ℓn()+ R ℓn(). Выразим отношение объёмов из уравнения Клапейрона: =Т₂ После подстановки этого отношения в выражение для изменения энтропии получим:

 

ΔS= C_р ℓn() - R ℓn().

 

При выводе этой формулы было учтено уравнение Майера: C_р=C_V+R.

По условию задачи с газом происходит изотермический процесс, значит Т₂=Т₁ и тогда ΔS= - R ℓn(). Молярная масса водорода μ известна. Подставив числовые данные и произведя расчёт, получим: ΔS= 17,3 Дж/К.

 

 

Пример 6.3. Найти изменение энтропии при нагревании 100 г воды от 0 до 100°C и последующем превращении воды в пар при той же температуры.

Решение. Формула для изменения энтропии имеет вид:

, где dQ – малое изменение энтропии при температуре Т.

При бесконечно малом изменении dT температуры нагреваемого тела затрачивается теплота: dQ=mcdT, где m – масса тела, c – его удельная теплоёмкость.

Подставив dQ в формулу для изменения энтропии, получим, получим, что при нагревании воды

 

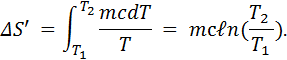
Произведём вычисления: ΔS=132 Дж/К.

При вычислении изменения энтропии в процессе превращения воды в пар при той же температуре постоянная температура Т может быть вынесена за знак интеграла:

 

где λ – удельная теплота парообразования. Подставим числовые значения и после вычислений получим, что при парообразовании ΔS=605 .

Полное изменение энтропии при нагревании воды и последующем превращении её в пар: ΔS=ΔS'+ΔS" =737 .

 

Раздел 7. Реальные газы.

 

Пример 7.1. В баллоне ёмкостью V=20 л находится m=1,1 кг углекислого газа при температуре 13ºC (Т=286 К). Определить давление газа в баллоне, пользуясь уравнением Ван-дер-Ваальса и уравнением состояния идеального газа.

Решение. Запишем уравнение Ван-дер-Ваальса для произвольной массы m газа:

 

 

Решая это уравнение относительно давления p, получим:

 

 

Если считать углекислый газ идеальным, то давление можно найти из уравнения Клапейрона-Менделеева:

р_ид = .

 

Здесь μ – молярная масса углекислого газа; R – универсальная газовая постоянная; a = 36 и b=0,043·10^-3 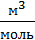– взятые из таблиц постоянные Ван-дер-Ваальса для углекислого газа.

Подставив в полученные формулы числовые данные и произведя вычисления, получим: р=25,93 · 10⁵ Па, р_ид = 29,71 · 10⁵ Па.

 

 

Пример 7.2. Вычислить для углекислого газа значения постоянных a и b в уравнении Ван-дер-Ваальса, зная его критические давление р_к =73,9 ·10⁵ Па и температуру Т_к =304,1 К.

Решение. Уравнение Ван-дер-Ваальса [p+ 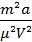]·(V- )= можно записать иначе. После несложных преобразований его можно привести к виду:

 

V_μ³ - (b+ 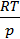)V_μ² + - =0.

 

Здесь V_μ – молярный объём газа, связанный с объёмом по формуле V= . Это алгебраическое уравнение третьей степени относительно объёма. При заданных значениях температуры и давления оно имеет три решения, которые все могут быть вещественными, либо два из них могут быть комплексными, а одно вещественным. Поскольку объём может быть только вещественным, комплексные решения не имеют физического смысла.

При критической температуре все три корня уравнения Ван-дер-Ваальса одинаковы и равны критическому объёму. Поэтому

 

V_μ³ - (b+RT_к/p_к)V_μ² + aV_μ/p_к - ab/p_к=0.

 

Это уравнение должно быть тождественно уравнению:

 

(V_μ-V_к)³ = V_μ³ - 3V_μ²V_к + 3V_μ V_к² - V_к³=0.

 

Здесь V_к – объём одного моля газа при критических давлении температуре. Сравнивая коэффициенты при членах обоих уравнений, содержащих одинаковые степени V_μ, можем записать три следующих соотношения:

 

3V_к =b+ ; 3V_к² = ; V_к = .

 

Используя эти соотношения, можно найти зависимость между критическими параметрами вещества и соответствующими значениями постоянных в уравнении Ван-дер-Ваальса: Т_к = ; V_к =3b; p_к = , или

 

a=3V_к²p_к; b= ; R=

 

Из последнего соотношения выразим критический объём: V_к = . Подставляя это выражение в первые два соотношения, найдём:

 

a= ; b=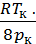

 

После вычислений получим: а= 0,36 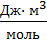; b=0,043 .

 

 

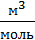⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: