 |
Раздел 3. Уравнение состояния идеального газа. Газовые смеси.
|
|
|
|
Пример 3.1.Найти молярную плотность идеального газа при нормальных условиях.
Решение. Молярная плотность это число молей газа в единице объёма, равное 
. Это отношение можно выразить из уравнения состояния идеального газа: pV=νRT. Молярная плотность равна: 
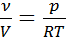. Подставляя в эту формулу значения давления и температуры при нормальных условиях (соответственно 100 кПа и 273 К), получим, что независимо от химической природы идеального газа его молярная плотность при нормальных условиях 44,64 
.
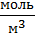Пример 3.2. Под каким давлением находится кислород (молярная масса μ=0,032 
) в баллоне объёмом V=10 л и чему равна суммарная кинетическая энергия всех его молекул при условии, что концентрация газа n=2·1025 м-3, а средняя квадратичная скорость молекул кислорода vкв =103 
.
Решение. 1) Для нахождения давления газа p воспользуемся уравнением Клапейрона-Менделеева (уравнением состояния идеального газа): pV= 
RT, из которого следует, что p=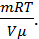 
Массу газа можно выразить через известные величины следующим образом: m=Nm0 , где N=nV – число молекул газа, m0 = 
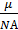– масса одной молекулы кислорода. NА - число Авогадро.
Таким образом,
m=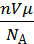 
→ 
= 
.
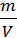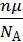Температуру газа можно определить из выражения для средней квадратичной скорости молекул (см. выше):
T= vкв ²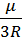 
.
Подставив полученные выражения в формулу для расчёта давления, окончательно получим:
p=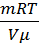 
= vкв ² μ 
.
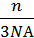После подстановки числовых данных и расчёта получим: p=354 кПа.
2) Суммарная кинетическая энергия всех молекул газа Eкин=(
)kTN, где i – число степеней свободы молекул (для кислорода, являющегося двухатомным газом, i=5); k – постоянная Больцмана; T – абсолютная температура; N – число молекул. Поскольку число молекул можно найти по формуле N=(
) NА, а также с учётом того, что R=k NА, получим:
|
|
|
Eкин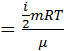 
.
Сравнивая это с уравнением состояния, можно заметить, что Eкин= 
pV. Подставив числовые данные и произведя расчёт, получим: Eкин=8,86 кДж.
Пример 3.3. В баллоне объёмом V=5 л находится смесь кислорода и водорода под давлением p=кПа при температуре 27°C. Масса кислорода в три раза больше массы водорода (m1=3m2). Найти число молекул кислорода N1 и число молекул водорода N2 в этом баллоне. Молярная масса кислорода μ1= 0,032 , молярная масса водорода μ2=0,002 .
Решение. По закону Дальтона давление смеси газов равно сумме давлений каждого газа в отдельности (парциальных давлений): p=p1+p2. При этом каждый газ занимает объём, равный объёму баллона. Из уравнения Клапейрона-Менделеева, записанного для каждого газа в отдельности, можно выразить парциальные давления. Складывая их, получим общее давление:
p=(
)·[ 
+ 
].
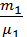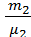С учётом соотношения масс, получим:
p=(m2 )·[ 
].
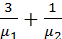Массу водорода можно выразить следующим образом: m2 =μ2 N2 /NА. Подставив это в уравнение для p и выразив затем число молекул водорода, с учётом того, что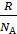 
=k, можно получить:
N2 = 
Используя соотношение масс газов, найдём число молекул кислорода:
N1=3μ2 
.
Переведя числовые данные в единицы измерения СИ и произведя расчёт, получим: N1= 1022, N2=5·1023 молекул.
Пример 3.4. Найти молярную массу смеси, состоящей из 25 г кислорода и 75 г азота.
Решение. Введём обозначения: m1, ν1, μ1 – масса, количество вещества и молярная масса кислорода; m2,ν2, μ2 – масса, количество вещества и молярная масса азота; mсм, νсм, μсм – масса, количество вещества и молярная масса смеси.
Молярную массу смеси можно найти как отношение массы с меси к количеству вещества смеси:
μсм = 
.
Масса смеси равна сумме масс компонентов: mсм = m1 + m2. Количество вещества смеси
νсм = ν1 + ν2 =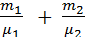 
.
|
|
|
С учётом двух последних выражений получим:
μсм =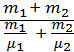 
.
После подстановки числовых данных и последующих расчётов получим: μсм = 0,0289 .
Пример 3.5. Воздушный шар диаметром D=8 м удерживается верёвкой, натянутой вертикально. Насколько изменится натяжение верёвки, если температура окружающего воздуха понизится с t1 = 27°C до t2 =7°C? Атмосферное давление pатм нормальное (100 кПа). Молярная масса воздуха μ=0,029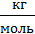 
.
Решение. На воздушный шар действуют три силы: выталкивающая Fвыт (вверх), сила тяжести mg (вниз) и сила натяжения верёвки FН (вниз). Из-за понижения температуры изменится плотность воздуха, следовательно, изменится выталкивающая сила. При равновесии шара силы компенсируются, поэтому для двух состояний газа (до и после понижения температуры) на основании первого закона Ньютона можем записать: Fвыт1 =mg+FН1; Fвыт2 =mg+FН2. Изменение силы натяжения
ΔF =FН2 - FН1= Fвыт2 - Fвыт1 = ρ2 gV – ρ1 gV,
где ρ1 и ρ2 – плотности газа при температурах Т1 и Т2, V= 
– объём шара. Плотности газа можно найти из уравнения Клапейрона – Менделеева, записанного в форме: p= 
. Тогда ρ1 =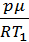 
,
ρ2 =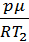 
.
Подставляя формулы объёма и плотности в выражение для ΔF, после несложных преобразований получим:
ΔF={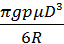 
}·(1/T2 -1/T1). Вычисления дают: ΔF= 0,4 Н.
|
|
|
