 |
Раздел 4. Основы термодинамики.
|
|
|
|
Пример 4.1. Двухатомный газ под давлением p=150 кПа и при температуре t=27°C занимает объём V=100 л. Определить теплоёмкость этого газа при постоянном объёме cV и при постоянном давлении cp.
Решение. Теплоёмкость – это количество теплоты, которое нужно передать всему веществу для изменения его температуры на 1 К. Молярные теплоёмкости газа при постоянном объёме и при постоянном давлении соответственно выражаются через универсальную газовую постоянную R:
CV = 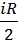 и Cp =(i+2)
и Cp =(i+2)  .
.
В случае двухатомного газа число степеней свободы молекул i=5.
С учётом сказанного, для теплоёмкостей газа можно записать:
cV = CV  = im
= im 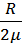 ; cp = Cр
; cp = Cр  = (i+2)m
= (i+2)m 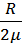 .
.
Из уравнения Клапейрона-Менделеева pV= 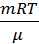 находим, что
находим, что 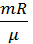 =
= 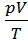 . Тогда уравнения для теплоёмкостей принимают вид: cV =
. Тогда уравнения для теплоёмкостей принимают вид: cV = 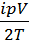 ;
;
cp =(i+2)p  . Производя вычисления по этим формулам, получим: cV =125 Дж/К, cp =175 Дж/К.
. Производя вычисления по этим формулам, получим: cV =125 Дж/К, cp =175 Дж/К.
Пример 4.2. двухатомный газ занимает объём V=10 см3 и находится под давлением p=40 мм рт. ст. Найти внутреннюю энергию этого газа U. Какая часть этой энергии приходится на долю поступательного, а какая на долю вращательного движения молекул?
Решение. Обозначим Uпост и Uвращ внутреннюю энергию газа, приходящуюся соответственно на поступательное и вращательное движение молекул. Внутренняя энергия газа, имеющего i степеней свободы молекул, определяется выражением: U=  , где m – масса газа, μ – его молярная масса, R – универсальная газовая постоянная, T – абсолютная температура. На основании уравнения Клапейрона-Менделеева можно заменить
, где m – масса газа, μ – его молярная масса, R – универсальная газовая постоянная, T – абсолютная температура. На основании уравнения Клапейрона-Менделеева можно заменить 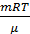 на произведение pV. Тогда для внутренней энергии получим формулу: U=
на произведение pV. Тогда для внутренней энергии получим формулу: U=  . Подставив данные, переведённые в СИ, с учётом того, что i=5, получим:U= 0,133 Дж.
. Подставив данные, переведённые в СИ, с учётом того, что i=5, получим:U= 0,133 Дж.
Для энергии поступательного и вращательного движения всех молекул газа соответственно справедливы формулы: Uпост =iпост 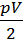 , Uвращ =iвращ
, Uвращ =iвращ 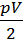 . Известно, что для любого газа iпост =3. Для двухатомного газа iвращ =2.
. Известно, что для любого газа iпост =3. Для двухатомного газа iвращ =2.
|
|
|
Из предыдущих формул видно, что  =
= 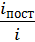 ;
; 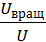 =
= 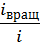 . Таким образом получим, что на поступательное движение приходится 0,6 (или 60%) внутренней энергии газа, а на вращательно движение – 0,4 (или 40 %) этой энергии.
. Таким образом получим, что на поступательное движение приходится 0,6 (или 60%) внутренней энергии газа, а на вращательно движение – 0,4 (или 40 %) этой энергии.
Пример 4.3. В цилиндре объёмом V=6 л под поршнем, занимающим среднее положение, находится водород Н2 при атмосферном давлении (р0=100 кПа). При нагревании газ расширяется при постоянном давлении, в результате чего поршень поднимается вверх до упора, после чего давление газа постепенно возрастает в два раза. Определить количество теплоты, переданное газу. Трением поршня о стенки сосуда, а также весом поршня и его толщиной пренебречь.
Решение. На первом этапе газ расширяется от V1 = 3 л до V2 = 6 л при постоянном давлении, т.е. происходит изобарический процесс, а затем нагревается при постоянном объёме, т.е. идёт изохорический процесс. Суммарное количество теплоты, переданное газу, найдём как сумму количеств теплоты, переданных при изобарическом Qр и изохорическом QV процессах.
Q=Qр +QV =  Cp (T2 –T1) +
Cp (T2 –T1) +  CV(T3-T2) =
CV(T3-T2) =
= m(i+2)R 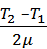 + miR
+ miR 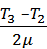 ,
,
где i=5 (число степеней свободы двухатомного газа), m – масса газа, μ – молярная масса водорода, R – универсальная газовая постоянная. Выразив температуры T1,T2,T3 из уравнения Клапейрона-Менделеева, полученное выражение для Q можно представить в виде:
½{(i+2)(p0V2 – p0V1)+i(p2V2 – p0V2)} = ½{(i+2) p0 (V2 – V1)+i(p2 – p0 )V2}.
Произведя вычисления по этой формуле, получим, что суммарное количество теплоты, переданное газу в ходе двух процессов, Q = 2,55 кДж.
Пример 4.4. В вертикальном цилиндре под тяжёлым поршнем находится кислород массой m=2 кг. Для повышения температуры газа на ΔT= 5 К ему сообщили Q=9160 Дж теплоты. Найти удельную теплоёмкость кислорода при постоянном давлении cр, работу А, совершённую газом при расширении, и приращение его внутренней энергии ΔU. Молярная масса кислорода μ=0,032 кг/моль.
|
|
|
Решение. Поскольку масса поршня и атмосферное давление не изменяются, здесь имеет место изобарический процесс. Поэтому переданное газу количество теплоты выразится формулой: Q=cр m ΔT. Отсюда cр =Q/(m ΔT). Изменение внутренней энергии кислорода найдём по формуле: ΔU=imR ΔT/(2μ), где i=5 – число степеней свободы двухатомной молекулы кислорода, R – универсальная газовая постоянная. Работу газа найдём из первого начала термодинамики как разность полученного количества теплоты и изменения внутренней энергии: A= Q – ΔU.
Произведя вычисления, получим: cр =916 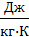 , ΔU= 6492 Дж, А=2668 Дж.
, ΔU= 6492 Дж, А=2668 Дж.
Пример 4.5. Азот N2 массой m=10 г расширяется изотермически при температуре t=-20°C (Т=253 К). При этом его давление изменяется от р1 =202 кПа до р2 =101 кПа. Найти работу расширения, изменение внутренней энергии азота и количество теплоты, сообщённое газу.
Решение. Изменение внутренней энергии газа определяется изменением температуры: ΔU=cm ΔT, где c – удельная теплоёмкость, m – масса газа. Поскольку в изотермическом процессе изменение температуры ΔT=0, внутренняя энергия газа не изменяется, т.е. ΔU=0.
Работа газа в изотермическом процессе, как известно, определяется выражением:

Подставим в подынтегральное выражение давление, выраженное из уравнения Клапейрона-Менделеева: p= 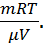 Тогда, проведя интегрирование, получим:A=
Тогда, проведя интегрирование, получим:A=  ln(
ln(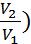 .
.
По закону Бойля-Мариотта отношение объёмов газа при изотермическом процессе можно заменить обратным отношением давлений:  . Тогда получим: A=
. Тогда получим: A=  ln(
ln(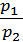 ). Подставив числовые данные, рассчитаем работу газа. Получим: A ≈ 520 Дж.
). Подставив числовые данные, рассчитаем работу газа. Получим: A ≈ 520 Дж.
Количество теплоты, сообщённое газу, найдём из первого начала термодинамики: Q=ΔU+A, или, поскольку в изотермическом процессе ΔU=0, для теплоты получим: Q=A≈520 Дж.
|
|
|


