 |
Багаточленом над розширеним полем називається багаточлен виду
|
|
|
|
Білет №23
1. Кінцеві поля Галуа, основні терміни і визначення
2. Загальна характеристика комутаційного обладнання
Відповіді
1) Розширеним кінцевим полем Галуа називається поле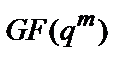 
, де 
– просте число, а 
– ціле позитивне число. Елементами такого поля є багаточлени ступеня меншої з коефіцієнтами з 
. При цьому операції додавання, віднімання, множення і ділення виконуються в кільці багаточленів по модулю, так називаного багаточлена 
, що породжує, ступеня , який має вид
, 
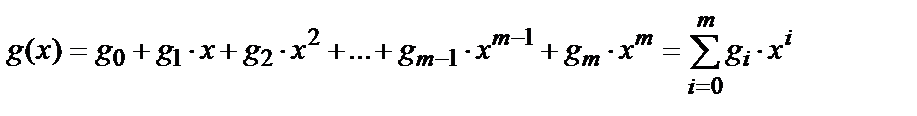. (1)
Просте число 
називається характеристикою розширеного поля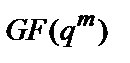 
, а ненульове ціле позитивне число – ступенем його розширення.
Багаточлен (1) є що неприводиться, тобто не може бути розкладений на множники – багаточлени з коефіцієнтами з поля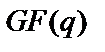 
. Багаточлени, що неприводяться, аналогічні простим числам і діляться без залишку тільки на себе і «1». Таблиці багаточленів, що неприводяться, приведені зокрема в літературі.
Для більш детального розгляду кінцевих полів у виді кілець багаточленів наведемо основні поняття і визначення.
Багаточленом над розширеним полем називається багаточлен виду
. (2)
де 
– формальна перемінна,
– цілі числа, що належать полю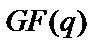 
( 
).
Нульовим багаточленом називається багаточлен виду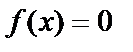 
.
Приведеним багаточленом називається багаточлен, старший коефіцієнт якого дорівнює «1», тобто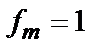 
. З (1) видно, що багаточлен 
, який породжує, є приведеним.
Ступенем ненульового багаточлена 
називається максимальний індекс ненульового коефіцієнта 
і позначається 
.
Простим багаточленом називається приведений багаточлен, що неприводиться.
Відомо, що кільце багаточленів по модулю багаточлена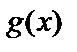 
є полем тільки тоді, коли 
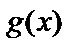простій. Саме такі багаточлени використовуються в якості тих, що породжують.
|
|
|
Елементами розширеного поля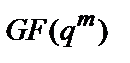 
є всі багаточлени, отримані шляхом підстановки всіх можливих елементів поля 
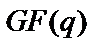як коефіцієнти ( 
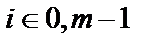) багаточлена виду (2).
Білет №24
1. Основні властивості розширених кінцевих полів Галуа
2. Загальна характеристика еталонної моделі взаємодії відкритих систем
Відповіді
Властивості розширених кінцевих полів Галуа
Поля Галуа володіють цілим рядом важливих практичних властивостей, що знайшли широке використання при побудові й описі циклічних кодів, кожний з яких може бути представлений багаточленом від формальної перемінної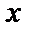 
.
Код є циклічним, якщо разом з кодовим словом 
він також містить багаточлен 
(результат зсуву коду 
на один розряд вправо з приміщенням старшого розряду на місце молодшого).
Коротко охарактеризуємо деякі властивості полів Галуа.
1. Для будь-якого простого 
і цілого позитивного 
існує розширене поле 
з 
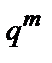елементами.
2. Будь-які два поля Галуа з однаковою кількістю елементів ізоморфні.
3. Кожне поле Галуа містить хоча б один примітивний елемент.
Для опису розширених кінцевих полів Галуа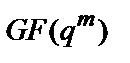 
часто використовують, так називані, примітивні елементи. Примітивним елементом поля 
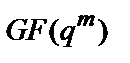називається такий елемент 
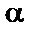поля, що дозволяє задати всі інші елементи поля (за винятком «0») у виді цілого ступеня .
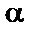Приклад 4.
Задати розширене кінцеве поле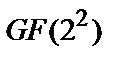 
, що складається з елементів {0, 1, 
, 
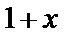}, у виді ступенів примітивного елемента 
. У якості що породжує використовувати багаточлен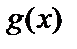 
виду (3).
Неважко показати, що справедливо рівності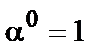 
й 
і отже поле 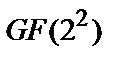може бути задане у виді 
.
|
|
|
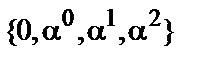