 |
Вправа 2.3. Саме такі багаточлени використовуються на практиці для відшукання багаточленів , що породжують, виду (1) при формуванні циклічних кодів.
|
|
|
|
Вправа 2. 3.
Довести, що розширене кінцеве поле Галуа 
з багаточленом 
, що породжує, може бути задане у виді ступенів примітивного елемента 
.
4. Над кожним полем Галуа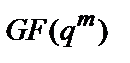 
існує хоча б один примітивний багаточлен довільного позитивного ступеня (не більше 
).
Прокоментуємо цю властивість.
Нехай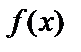 
– багаточлен, що неприводиться, з коефіцієнтами у виді елементів поля 
(тобто 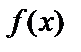– елемент розширеного поля 
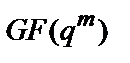). Відомо, що такий багаточлен завжди можна розкласти на співмножники, використовуючи елементи деякого розширення. Нехай 
його корінь з розширення 
. Тоді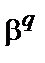 
, 
, 
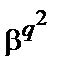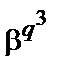, … також будуть коренями багаточлена 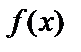. У цьому випадку багаточлен 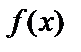називають мінімальною функцією від або мінімальним багаточленом. Якщо є примітивним елементом ( 
), то 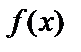називається примітивним багаточленом.
Саме такі багаточлени використовуються на практиці для відшукання багаточленів, що породжують, виду (1) при формуванні циклічних кодів.
Приклад 5.
Відомо розширене кінцеве поле 
з елементами {0, 1, 
, 
, 
, 
, 
, 
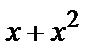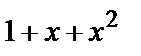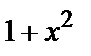} по модулю примітивного багаточлена 
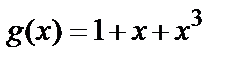, що породжує. Примітивний елемент дорівнює 
й отже поле представимо у виді {0, 
, 
, 
, 
, 
, 
, 
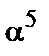} Довести, що значення 
, , 
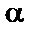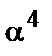є коренями багаточлена 
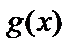, приймаючи в увагу, що 
.
Доказ проведемо методом підстановки. Елемент 
поля є коренем багаточлена 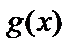оскільки
( 
).
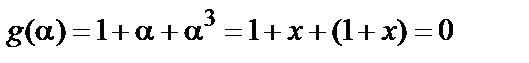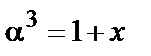Аналогічно проведемо доказ для елементів поля 
, 
:
;
( 
).
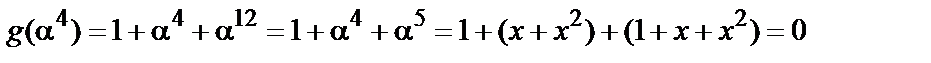Помітимо, що якщо 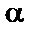, , 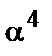є коренями невідомого примітивного багаточлена 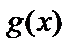, то він може бути знайдений зі співвідношення
.
Таким чином, довільний мінімальний багаточлен 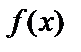з коефіцієнтами у виді елементів поля 
завжди може бути представлений у виді добутку
,
де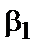 
, 
, …, 
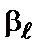– деяка сукупність елементів розширеного кінцевого поля 
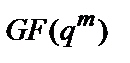(підходи до відшукання таких сукупностей елементів поля будуть обговорені нижче).
|
|
|
5. Для довільного багаточлена 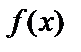з коефіцієнтами у виді елементів поля 
справедливо рівність 
.
Справедливість цієї рівності випливає з того, що всі багаторазові співмножники в 
мають коефіцієнти кратні 
і тому в поле 
дорівнюють нулеві.
Приклад 6.
.
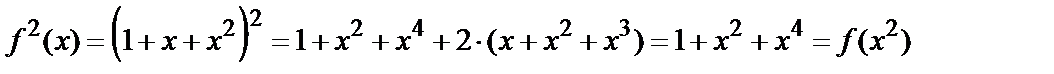(ВАЖЛИВЕ ВИЗНАЧЕННЯ)
Порядком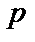 
( 
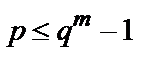) елемента 
( 
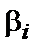) розширеного кінцевого поля Галуа 
називається найменше значення ступеня ( 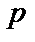– ціле позитивне число), при якій 
.
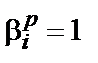6. Якщо 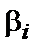є коренем деякого мінімального багаточлена 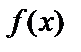, то 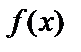нацело поділяє багаточлен 
за умови, що 
.
7. Корені багаточлена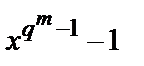 
збігаються з ненульовими елементами розширеного кінцевого поля 
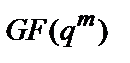(елементами мультиплікативної групи поля, що включає всі елементи крім 
), тобто 
.
(ЗВЕРНУТИ УВАГУ)
Циклічний код довжини 
над полем 
існує для кожного багаточлена 
, що породжує, який поділяє багаточлен 
( 
). При цьому може бути знайдений з розкладання багаточлена на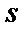 
простих множників (мінімальних багаточленів)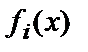 
,
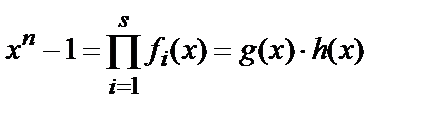де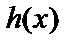 
– так називаний перевірочний багаточлен.
Видно, що багаточлен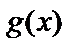 
, що породжує, поділяє (нацело) багаточлен 
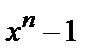і дорівнює 
(тут 
– довільний номер (номера) мінімального багаточлена з 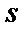наявних простих множників полінома ). Породжуваний багаточленом 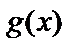циклічний код складається з багаточленів, що поділяються на кожний з 
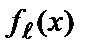(нагадаємо, що для двійкового коду поліном дорівнює поліномові 
).
У такий спосіб багаточлен, що породжує, можна знайти знаючи всі мінімальні багаточлени розширеного кінцевого поля.
Для опису способу відшукання всіх мінімальних багаточленів у розширеному полі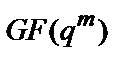 
приведемо кілька визначень.
Елементи поля 
, що є коренями одного мінімального багаточлена, називаються сполученими.
|
|
|
