 |
1) Коды Боуза-Чоудхури-Хоквингема (БЧХ).
|
|
|
|
1) Коды Боуза-Чоудхури-Хоквингема (БЧХ).
Коды Боуза-Чоудхури-Хоквингема (БЧХ-коды) представляют собой обширный класс циклических кодов, позволяющих исправлять пакеты ошибок размера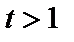 
, и занимают заметное место в теории и практике кодирования. Они представляют особый интерес в связи с тем, что при их использовании исправление ошибок большой кратности удается реализовать более эффективными и простыми методами в сравнении с другими циклическими кодами, не говоря уже о произвольных линейных кодах.
Примечание. Боуз и Рой Чоудхури в 1960 году, а Хоквингем в 1959 году нашли большой класс кодов, исправляющих кратные ошибки (коды БЧХ). Открытие кодов БЧХ привело к облегчению поиска практически реализуемых кодеров и декодеров.
Кодами БЧХ принято называть циклические коды, для которых в качестве корней порождающего многочлена 
выступают 
последовательных степеней произвольного элемента 
, причем необязательно примитивного [1].
В этом случае порождающий многочлен определяется из соотношения
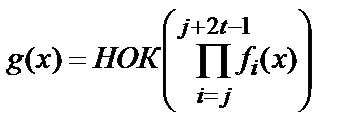, (4)
где 
– одна из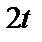 
подряд следующих степеней ( 
);
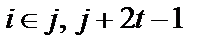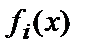– минимальный многочлен элемента 
, (НОК – наименьшее общее кратное), корнями которого являются все элементы класса сопряженных элементов (мультипликативной подгруппы) поля
,
где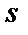 
– наименьшее целое ( 
) для которого справедливо равенство 
.
Длина кода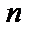 
равна такому порядку элемента 
, для которого справедливо равенство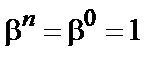 
.
Доказана следующая теорема о границе БЧХ, которая определяет нижнюю границу для минимального кодового расстояния, справедливой для всех циклических кодов.
Теорема. Параметры циклического блокового кода 
-кода БЧХ над полем 
, заданного порождающим многочленом 
вида (4) с корнями удовлетворяют условиям
|
|
|
, 
. (5)
В литературе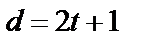 
называют конструктивным кодовым расстоянием. Реальное кодовое расстояние в соответствии с (4) может быть больше конструктивного.
Таким образом, приведенные выше рассуждения позволяют однозначно задать конструктивные характеристики циклического кода – его -параметры, что является практически важным обстоятельством при обосновании выбора помехоустойчивых кодов в тех или иных разновидностях телекоммуникационных систем.
Пример 5.
Определить возможные параметры двоичных кодов БЧХ над полем ( 
) со степенью расширения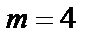 
.
Решение.
Известны элементы расширенного поля 
, заданные в виде степени примитивного элемента 
– { 
, 
, 
, 
, …, 
, 
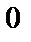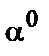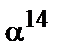}, а также классы сопряженных элементов (мультипликативные подгруппы) поля, соответствующие им минимальные многочлены 
и порядки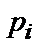 
( 
):
- 
; 
; 
;
- 
; 
; 
;
- 
; 
; 
;
- 
; 
; 
;
- 
; 
; 
.
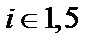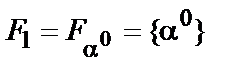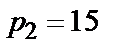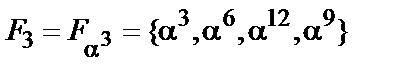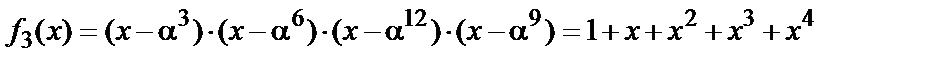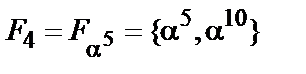1. При 
очевидно, что 
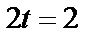(в мультипликативной подгруппе только два элемента с подряд следующими степеням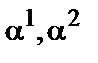и – 
) и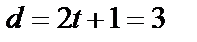 
. Число проверочных разрядов (разрядов четности) 
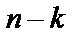равно степени полинома 
, т. е. 
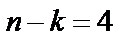, а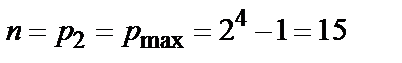 
. Следовательно многочлен 
порождает ( 
)-код БЧХ (код Хэмминга).
2. При 
в мультипликативной подгруппе { , , 
, 
, 
, 
, 
, 
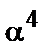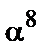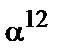} четыре элемента с подряд следующими степенями 
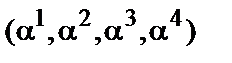, следовательно 
и 
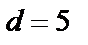. Порядок такой мультипликативной подгруппы равен 
и следовательно 
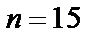. Видно, что 
и поэтому многочлен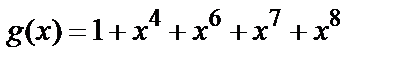 
порождает ( 
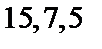)-код БЧХ.
3. При 
в мультипликативной подгруппе { , , , , 
, , , , 
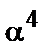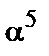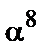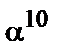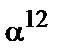, } шесть элементов с подряд следующими степенями 
, следовательно 
и 
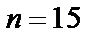. Порядок такой мультипликативной подгруппы равен и следовательно . Видно, что 
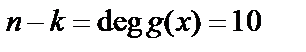и поэтому многочлен 
порождает (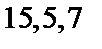 
)-код БЧХ.
|
|
|
Варианты 1-3 являются примерами примитивных кодов БЧХ (кодов примитивной длины). Коды БЧХ не исчерпываются такими кодами.
4. Пусть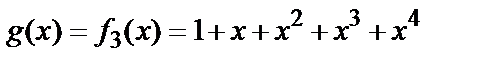 
. Обозначим через 
, тогда мультипликативная подгруппа поля примет вид 
. Видно, что 
и 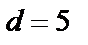. Число разрядов четности равно 
Порядок класса и следовательно длина кода равна 
. Таким образом многочлен 
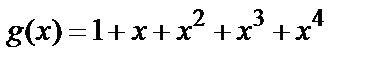порождает ( 
)-код БЧХ.
Тривиальный ( )-код БЧХ является примером непримитивных циклических кодов (кодов непримитивной длины). Длина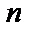 
таких кодов равна 
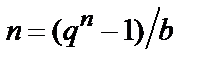, где 
– произвольное положительное целое, делящее нацело 
.
2) Загальні відомості про телекомунікаційні мережі
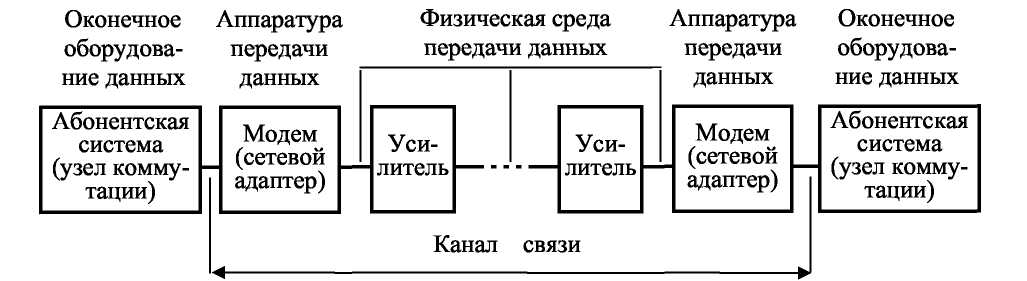
У загальному випадку телекомунікаційну мережу утворюють канали зв'язку і вузли комутації (ВК).
Вузли комутації являють собою спеціалізовані ЕОМ, мости, комутатори, маршрутизатори або модульні концентратори, що керують вибором маршрутів передачі даних у мережі.
Вузли комутації і абонентські системи узагальнено називаються кінцевим устаткуванням даних (КУД).
Каналом зв'язку називають фізичне середовище і апаратуру передачі даних (АПД), що здійснюють передачу інформації від одного вузла комутації до іншого або між вузлом комутації і абонентською системою.
Фізичне середовище передачі даних - це простір або матеріал, що забезпечують поширення інформаційних сигналів.
Як фізичне середовище передачі даних у телекомунікаційних мережах можуть використовуватися:
- провідні (повітряні) лінії зв'язку - не ізольовані проводи, натягнуті між телеграфними стовпами, що висять у повітрі;
- кабельні лінії зв'язку - кабелі на основі кручених пар мідних проводів, коаксіальні кабелі, волоконно-оптичні кабелі і т. п.;
- радіоканали наземного і супутникового зв'язку.
Апаратура передачі даних - сукупність технічних засобів, призначених для перетворення дискретних сигналів, формованих передавальним КУД, у сигнали, передані по фізичних лініях зв'язку, і зворотного перетворення сигналів, що надходять по лініях зв'язку у приймаюче КУД.
В якості АПД використовуються модеми, мережні адаптери (мережні карти), оптичні модеми, пристрої підключення до цифрових каналів і т. п. При великій довжині ліній зв'язку АПД може включати проміжне устаткування у вигляді різних підсилювачів - формувачів переданих сигналів.
|
|
|
Склад каналу зв'язку телекомунікаційної мережі представлений на рис. 1.
|
Рис. 1. Склад каналу зв'язку
До основних характеристик телекомунікаційних мереж належать:
- пропускна здатність мережі або окремого каналу зв'язку;
- вірогідність передачі даних;
- надійність роботи.
Пропускна здатність мережі (каналу) — максимально можлива кількість інформації, що може бути передана по мережі (по каналу) за одиницю часу. Пропускна здатність виміряється в бітах у секунду (біт/с), у кілобітах у секунду (кбіт/с), у мегабітах у секунду (Мбіт/с), у гігабітах у секунду (Гбіт/с) і т. д.
Вірогідність передачі даних - імовірність перекручування кожного переданого біта інформації. Для провідних ліній зв'язку імовірність перекручування біта інформації складає 
, для кабельних - 
, для оптоволоконних ліній - 
.
Надійність - властивість телекомунікаційної мережі зберігати в часі у встановлених межах значення всіх параметрів, що характеризують здатність мережі виконувати необхідні функції в заданих умовах застосування.
|
|
|
