 |
Пример 1. Примечание. Из табл.1 видно, что столбцы проверочной матрицы циклического кода Хэмминга ( ) задаются элементами кольца многочленов (мультипликативной группы) расширенного конечного поля , т.е.
|
|
|
|
Пример 1.
Описать циклический ( 
)-код Хэмминга в терминах расширенного конечного поля Галуа 
.
Известны элементы расширенного конечного поля ( 
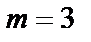) по модулю порождающего многочлена 
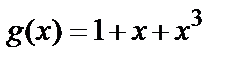, представленные в табл. 1.
Таблица 1
| Код | Многочлен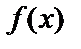 
| Степень примитивного элемента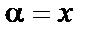 
| Столбец попроверочной матрицы  (систематический код)
|
| 0 0 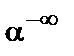0 |  или 0
| – | |
| 1 0 0 | 
| 
| |
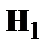
| 0 1 0 | 
| 
| 
|
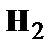
| 0 0 1 | 
| 
| 
|
| 1 1 0 | 
| 
| 
|
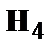
| 0 1 1 |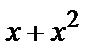 
| 
| 
|
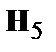
| 1 1 1 |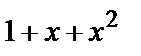 
| 
| 
|
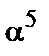
| 1 0 1 |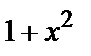 
| 
| 
|
Из табл. 1 видно, что столбцы проверочной матрицы 
циклического кода Хэмминга ( ) задаются элементами кольца многочленов (мультипликативной группы) расширенного конечного поля , т. е. 
– ( 
)-мерная матрица, описанная в терминах поля 
.
Для описания других циклических кодов (отличных от кодов Хэмминга) проверочная матрица может содержать произвольное число 
строк, состоящих из элементов поля , и иметь представление в виде (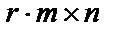 
)-мерной матрицы
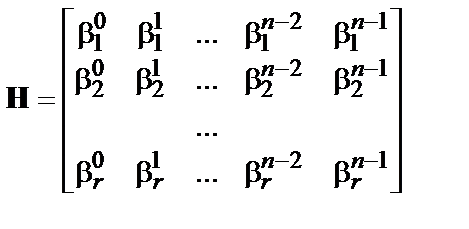, (2)
где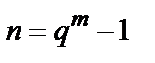 
, 
( 
).
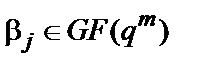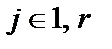Для полиномиального описания кодов Хэмминга, равно как и других циклических кодов, используются порождающие ( 
) и проверочные ( 
) многочлены. Для их задания необходимо знание классов сопряженных элементов (мультипликативных подгрупп) поля и соответствующих им минимальных многочленов.
Нетрудно показать, что для поля существует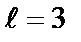 
класса ( 
, 
) сопряженных элементов, а соответствующие им минимальные многочлены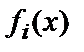 
равны соответственно:
1. класс по 
– 
; 
;
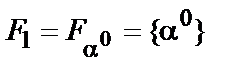2. класс по 
– 
; 
(именно этот многочлен использован в качестве порождающего в условиях примера 1 );
3. класс по 
– 
; 
.
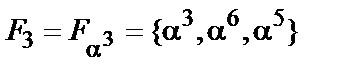Определим порядок элементов поля, входящих в классы сопряженных элементов. Напомним, что в общем случае он определяется из соотношения (7*) вида 
(здесь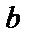 
– наибольший общий делитель 
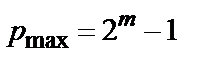и степеней 
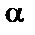всех элементов мультипликативной подгруппы).
|
|
|
Очевидно, что для классов поля 
, т. е. коды, которые могут быть «порождены» в этих условиях, являются кодами примитивной длины ( 
) или примитивными.
Значение порядка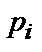 
определяет число различных (отличных от нуля) остатков от деления любой кодовой комбинации кода длины 
на соответствующий классу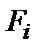 
минимальный многочлен 
.
Найдем соответствующий многочлену 
проверочный многочлен .
Из свойства полей Галуа, в соответствии с которым справедливо равенство
,
следует, что проверочный многочлен 
может быть найден из соотношения
. (3)
В условиях примера 1 проверочный многочлен равен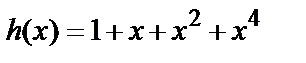 
–
|
|
|
|
|
|
|
|
|
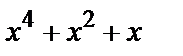
| Å |
| Å |
| Å |
|
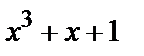
| Å |
Примечание.
Код Хэмминга, имеющий длину 
, является совершенным. Совершенным называется код, у которого радиус упаковки равен радиусу покрытия.
Пример 2.
Доказать, что любой двоичный циклический код Хэмминга является совершенным.
Решение.
Известно, что размерность кодового слова двоичного ( 
) циклического кода Хэмминга равна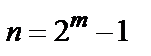 
. Следовательно полный набор кодовых последовательностей для 
-мерного двоичного кода («полный код») равен 
. Здесь 
является порядком порождающего многочлена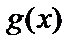 
и соответственно числом разрядов четности (проверочных разрядов).
Так как число информационных разрядов равно 
, то число «разрешенных» кодовых слов равно 
.
Исправляющая способность такого кода равна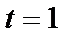 
, следовательно число -мерных кодовых последовательностей, отличающихся от одного «разрешенного» кодового слова на 
разряд равно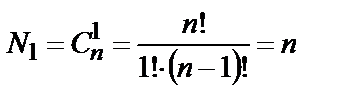 
, а от слов – равно 
.
Тогда число кодовых последовательностей, вошедших в «сферы» радиуса упаковки кода с центрами в в «разрешенных» кодовых словах равно 
.
|
|
|
Таким образом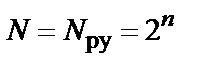 
и следовательно любой двоичный циклический код Хэмминга является совершенным.
Совершенные коды обладают рядом замечательных свойств. Одно из них состоит в том, что код дуальный совершенному является эквидистантным.
|
|
|
