 |
1) Елементи теорії.. 2) Амплітудна модуляція.
|
|
|
|
1) Елементи теорії.
Можливість створення цифрових систем зв'язку багато в чому визначається енергетичною ефективністю (ЕЕ) використовуваних методів формування і прийому сигналів, сукупність яких прийнято називати сигнально-кодовими конструкціями (СКК). Під ЕЕ розуміється мінімально припустиме значення відносини енергії сигналу до спектральної щільності потужності шуму, необхідне для забезпечення заданої вірогідності прийому повідомлення. Нижче розглядаються питання, що стосуються впливу на ЕЕ властивостей одного з елементів СКК – завадостійких кодів.
Основними аспектами проблеми завадостійкого кодування є:
1. побудова ефективних кодів, що виправляють помилки (складність полягає в тому, що звичайно потрібні довгі коди);
2. розробка методів кодування і декодування, що практично реалізуються;
3. відшукання надійного методу виправлення помилок.
Власне основна проблема теорії завадостійкого кодування вперше сформульована в роботі Шеннона*): знайти коди з великою відносною швидкістю  і з великою мінімальною кодовою відстанню
і з великою мінімальною кодовою відстанню 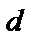 .
.
Визначення.
Кодова відстань або відстань Хеммінга – це «відстань» між будь-якими двома 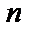 - мірними кодовими словами
- мірними кодовими словами 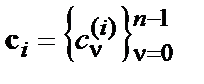 і
і  (
(  ,
, 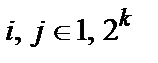 ), рівне числу
), рівне числу  розрядів, що відрізняються
розрядів, що відрізняються
 ,
,
де  – число інформаційних розрядів кодового слова.
– число інформаційних розрядів кодового слова.
Мінімальна кодова відстань  , що визначає спроможність коду, що виправляє, дорівнює
, що визначає спроможність коду, що виправляє, дорівнює
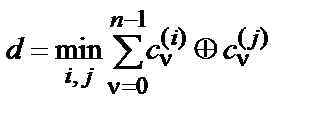 .
.
Ця проблема випливає з наступної теореми.
Теорема 1. Нехай 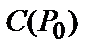 – пропускна спроможність дискретного симетричного каналу з імовірністю помилки
– пропускна спроможність дискретного симетричного каналу з імовірністю помилки  . Тоді для кожного
. Тоді для кожного  , якщо
, якщо 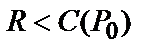 і
і 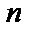 досить велико, існує (
досить велико, існує (  )- код з відносною швидкістю
)- код з відносною швидкістю  , імовірність помилки декодування якого
, імовірність помилки декодування якого 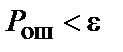 .
.
|
|
|
Теорема 1 доведена імовірнісними методами і не дає механізму для побудови кодів. Найбільший розвиток у теорії кодування одержали лінійні блокові коди, для яких справедлива наступна теорема.
Теорема 2 [2]. Якщо виконується рівність
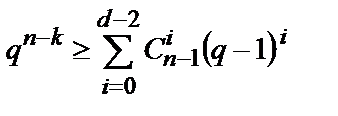 , (1)
, (1)
те існує лінійний (  )- код.
)- код.
Теорема 2 гарантує існування гарних лінійних кодів з (  ) параметрами, що задовольняють виразу (1), що одержало назву границі Варшамова-Гилберта. На практиці частіше використовують асимптотичні границі, що дають представлення про граничні кодові характеристики при нескінченно великій довжині коду. Прологарифмуємо вираз (1), одержимо
) параметрами, що задовольняють виразу (1), що одержало назву границі Варшамова-Гилберта. На практиці частіше використовують асимптотичні границі, що дають представлення про граничні кодові характеристики при нескінченно великій довжині коду. Прологарифмуємо вираз (1), одержимо
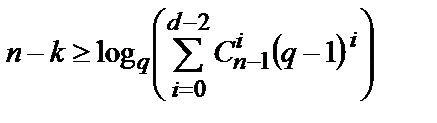 .
.
Для випадку двійкового коду (  ) співвідношення здобуває вид
) співвідношення здобуває вид
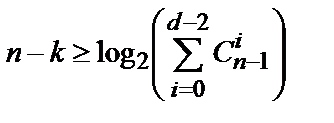 .
.
2) Амплітудна модуляція.
При амплітудній модуляції (AM) параметром, що змінюється (модулюється) за законом первинного сигналу несучого коливання 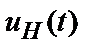 (1), є його амплітуда. Одержуване модульоване коливання має вигляд
(1), є його амплітуда. Одержуване модульоване коливання має вигляд
 ,
, 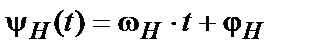 ,
,  . (2)
. (2)
Частота 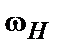 і фаза
і фаза 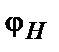 несучої залишаються незмінними.
несучої залишаються незмінними.
У загальному випадку функція 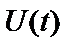 може бути як безперервної, так і дискретної і є що обгинає модульованого сигналу.
може бути як безперервної, так і дискретної і є що обгинає модульованого сигналу.
При так називаній повній амплітудній модуляції огинаючу можна представити як
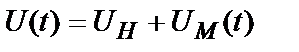 ,
, 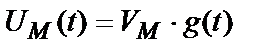 ,
, 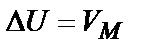 , (3)
, (3)
де  – нормована безрозмірна функція часу, що модулює, наприклад, гармонійне коливання;
– нормована безрозмірна функція часу, що модулює, наприклад, гармонійне коливання;
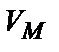 – амплітуда функції, що модулює;
– амплітуда функції, що модулює;
 – амплітуда несучої.
– амплітуда несучої.
Перепишемо 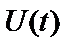 (3) у виді
(3) у виді
 , (4)
, (4)
де 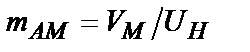 – коефіцієнт амплітудної модуляції ( глибина модуляції ), а аналітичне вираз (2) AM сигналу при
– коефіцієнт амплітудної модуляції ( глибина модуляції ), а аналітичне вираз (2) AM сигналу при 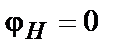 –
–
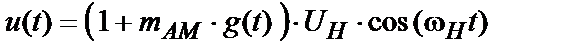 . (5)
. (5)
У найпростішому випадку гармонійного первинного сигналу (гармонійного закону модуляції) виду  вираз (5) прикмет вид
вираз (5) прикмет вид
 , (6)
, (6)
де 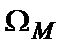 – частота модуляції.
– частота модуляції.
|
|
|
Епюр напруги амплітудно-модульованого коливання 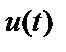 (6) приведений на рис. 2.
(6) приведений на рис. 2.
Чим більше амплітуда сигналу, що модулює, тим більше різниця між максимальним і мінімальним рівнями огинаючей АМ- сигналу, або глибина 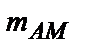 модуляції. Важливо знайти оптимальну величину глибини модуляції. Якщо значення
модуляції. Важливо знайти оптимальну величину глибини модуляції. Якщо значення  буде занадто низьким, скажемо, менш 0. 1 (це значить, що амплітуда сигналу-повідомлення мала), то корисний сигнал може бути помітно перекручений шумами. Прийом АМ- сигналу і відновлення вихідної інформації з огинаючей при цьому будуть утруднені наявністю сторонніх завад, що приведе до погіршення відносини сигнал/шум. З іншого боку, якщо
буде занадто низьким, скажемо, менш 0. 1 (це значить, що амплітуда сигналу-повідомлення мала), то корисний сигнал може бути помітно перекручений шумами. Прийом АМ- сигналу і відновлення вихідної інформації з огинаючей при цьому будуть утруднені наявністю сторонніх завад, що приведе до погіршення відносини сигнал/шум. З іншого боку, якщо  буде занадто великим, то в негативний напівперіод сигналу, що модулює, що обгинає може опуститися аж до осі абсцис, стосуючись неї. При подальшому збільшенні амплітуди сигналу, що модулює, форма спотворюється до такого ступеня, що демодульований сигнал не відповідає вихідної переданої інформації. Крім того, при великих значеннях
буде занадто великим, то в негативний напівперіод сигналу, що модулює, що обгинає може опуститися аж до осі абсцис, стосуючись неї. При подальшому збільшенні амплітуди сигналу, що модулює, форма спотворюється до такого ступеня, що демодульований сигнал не відповідає вихідної переданої інформації. Крім того, при великих значеннях  мінімальне значення амплітуди модульованого сигналу значно зменшується, і шуми знову можуть погіршувати якість прийому.
мінімальне значення амплітуди модульованого сигналу значно зменшується, і шуми знову можуть погіршувати якість прийому.
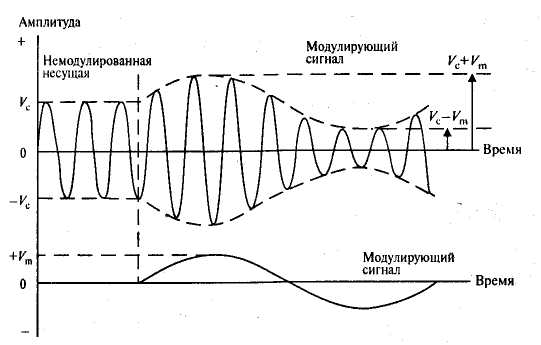 Рис. 2. Представлення амплітудно-модульованого сигналу в часовій області
Рис. 2. Представлення амплітудно-модульованого сигналу в часовій області
|
Практично зручно визначати глибину модуляції  по осцилограме по співвідношенню виду
по осцилограме по співвідношенню виду
 ,
,
де 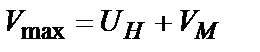 і
і  .
.
Використовуючи тригонометричну тотожність
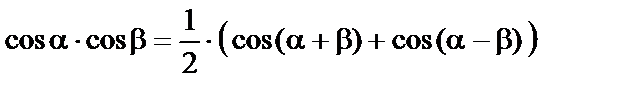 ,
,
спростимо вираз (6) і одержимо
 . (7)
. (7)
Рис. 3. Спектр АМ- сигналу 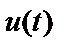 виду (6) виду (6)
|

|

|

|

|

|
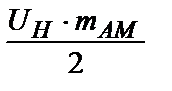
|

|
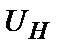
|
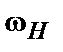 ,
, 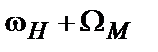 і
і 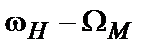 . Спектр сигналу (7) при гармонійній моделюючій напрузі показаний на рис. 3. Перший доданок у вираженні – несуче коливання. Йому відповідає на малюнку складового спектра на частоті
. Спектр сигналу (7) при гармонійній моделюючій напрузі показаний на рис. 3. Перший доданок у вираженні – несуче коливання. Йому відповідає на малюнку складового спектра на частоті 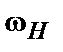 . Другий доданок гармоніка з частої
. Другий доданок гармоніка з частої 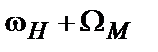 утворить верхню бічну складову спектра, доданок з частотою
утворить верхню бічну складову спектра, доданок з частотою 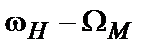 утворить нижню бічну.
утворить нижню бічну. |
|
|
У такий спосіб спектр АМ- сигналу розташовується в області допоміжного (несучого) коливання і містить несучу частоту і дві бічні смуги: верхню і нижню. Форма верхньої бічної частоти спектра такого сигналу аналогічна формі спектра сигналу, що модулює, а нижня смуга є «дзеркальним відбиттям» верхньої. Спектр модульованого сигналу виходить удвічі ширше спектра сигналу даних (інформаційного повідомлення). Ця особливість наочно ілюструється рис. 4.
Розглянутий вид амплітудної модуляції є так називаною повною амплітудною модуляцією, тому що в спектрі містяться несуче коливання й обидві бічні смуги. Разом з тим інформація про передане повідомлення не утримується в складовій на несучій частоті й енергетично вигідно придушити несучу без утрати можливого відновлення первинного сигналу на прийомній стороні.
 Рис. 4. Спектр АМ- сигналу (приклад)
Рис. 4. Спектр АМ- сигналу (приклад)
|
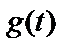 модулює, є періодичною, можна показати, що потужність сигналу з АМ за період
модулює, є періодичною, можна показати, що потужність сигналу з АМ за період 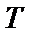 складається з потужності коливання на частоті
складається з потужності коливання на частоті 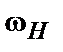 модулюємого сигналу, рівної
модулюємого сигналу, рівної 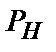 , і потужності
, і потужності  , що приходиться на обидві бічні складові. Отже на складову модулюємого коливання
, що приходиться на обидві бічні складові. Отже на складову модулюємого коливання 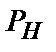 (не переносить інформації) на частоті
(не переносить інформації) на частоті 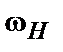 витрачається даремно велика частина енергії, причому при
витрачається даремно велика частина енергії, причому при  вона складає
вона складає  від загальної енергії, а на бічні складові (що переносять інформацію) приходиться тільки третя частина всієї потужності.
від загальної енергії, а на бічні складові (що переносять інформацію) приходиться тільки третя частина всієї потужності.
Таким чином, сигнал з повною амплітудною модуляцією енергетично невигідний.
|
|
|


