Найпростіші різновиди завадостійких кодів.

До числа простіших кодів відносяться деякі різновиди блокових кодів.

У комп'ютерних мережах для захисту інформації від помилок із блокових кодів найбільше широко використовуються коди з перевіркою за паритетом, коди Хеммінга і циклічні коди.

Коди з перевіркою на парність/непарність (за паритетом) є одними з простих видів кодів, що дозволяють виявляти одиночні помилки. Вони утворюються додаванням до переданої комбінації, що складається з  інформаційних елементів безнадлишкового коду, одного контрольного біта так, щоб загальна кількість одиниць у переданій комбінації була парною або непарною. Якщо контрольний біт обраний так, що результат підсумовування парний, то має місце позитивний паритет (even parity); якщо при додаванні контрольного біту результат буде непарним, то негативний паритет (odd parity). У підсумку загальна кількість бітів у переданій комбінації . На прийомній стороні роблять перевірку послідовності, що надходить, на парність (або непарність). При парному (непарному) числі одиниць передбачається, що помилок немає, і споживачеві видаються до інформаційних бітів, а контрольний елемент відкидається.

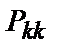Імовірність помилок, що виявляються, на парність (непарність) - розрядної кодової  комбінації залежить від довжини кодової комбінації і імовірності помилкового прийому одиничних елементів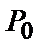

,

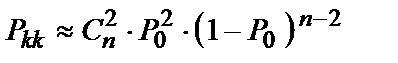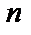де  – число сполучень з  по , а саме .

Ітеративні коди є різновидом кодів з перевіркою на парність. В англомовній літературі їх також називають прямокутними кодами (rectangular code). Вони характеризуються наявністю двох або більше систем перевірок усередині кожної кодової комбінації. Ітеративний код будується в такий спосіб. З елементів переданого блоку формується прямокутна матриця, що складається з  рядків і  стовпців. Потім до кожного рядка і кожного стовпця додаються біти паритету, що в результаті дає 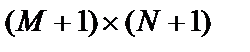 матрицю виду

,

де 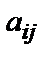 ( 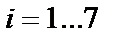; ) – інформаційні біти;

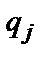 – перевірочні біти знаків (сукупності бітів ... ), що утворюють першу сукупність перевірок (звичайно вони отримуються як сума по модулю 2 бітів -го стовпця;

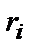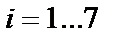 ( ) – контрольні біти, що є сумою по модулю 2 елементів -го рядка;

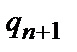 – перевірочний біт контрольних бітів ( ... ) знаків.

Кожен -й знак потрібно передавати послідовно, починаючи з першого біта ( ) і закінчуючи восьмим перевірочним .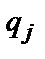

Наведений ітеративний код є найпростішим кодом цього класу з кодовою відстанню . Він виявляє помилки кратності до 3 і всі помилки непарної кратності, а також будь-який пакет помилок довжиною , де  – довжина рядка матриці коду. Основним недоліком ітеративних кодів, що використовують перевірки на парність по стовпцях і рядкам, є висока надмірність - близько 15%. Однак кодування і декодування таких кодів дуже просто реалізується програмними методами.

При більш жорстких вимогах по вірогідності передачі даних застосовується ітеративний код із трьома перевірками. Причому, третя додаткова перевірка на парність здійснюється по діагоналях матриці.

Код Хеммінга – один з найбільш ефективних кодів, що дозволяє виправляти одиночні помилки. Кодова відстань 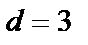. Цей код утворюється доповненням інформаційної частини переданого блоку, що складається з  бітів,  перевірочними елементами. При виборі довжини переданого блоку 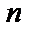 і кількості перевірочних елементів  керуються нерівністю

.

З огляду на те, що , нерівність може бути представлена у вигляді

,

де 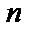 і  приймають тільки цілі значення. Нерівність є вихідним для визначення довжини кодової комбінації по заданому числу .

Найбільшого поширення набули коди Хеммінга з конструктивними параметрами, рівними ( ). Такі коди є простим різновидом циклічних кодів і будуть детально розглянуті в лекції, присвяченій опису циклічних кодів.