 |
2) Оптимальна обробка при розрізненні двійкових сигналів.
|
|
|
|
Прийом двійкових сигналів являє собою в загальному випадку статистичну задачу розрізнення двох сигналів хоча б по одному з його параметрів (амплітуді, частоті, фазі і т. п. ) при наявності завад.
Нехай на вхід прийомного пристрою надходить суміш 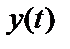 напруг сигналу
напруг сигналу  і флуктуаційної завади
і флуктуаційної завади  (адитивна завада) виду
(адитивна завада) виду
 ,
,  .
.
Чим більше апріорна інформація про параметри переданих сигналів, тим більше імовірність їхнього правильного розрізнення.
Будемо думати, що всі параметри сигналів (у тому числі і їхніх фазах) точно відомі. За результатами спостереження за реалізацією прийнятого коливання необхідно відповідно до обраного критерію оптимальності визначити який із двох можливих сигналів 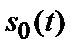 (відповідає символові «0») або
(відповідає символові «0») або  (відповідає символові «1») фактично був переданий.
(відповідає символові «1») фактично був переданий.
Сукупність можливих реалізацій прийнятих коливань 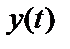 утворить простір прийнятих сигналів. Розіб'ємо його на дві області, що не перекриваються, одна з яких відповідає прийняттю
утворить простір прийнятих сигналів. Розіб'ємо його на дві області, що не перекриваються, одна з яких відповідає прийняттю 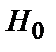 гіпотези про передачу
гіпотези про передачу 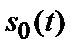 сигналу, а інша - прийняттю
сигналу, а інша - прийняттю  гіпотези про передачу
гіпотези про передачу  сигналу. Так при амплітудній модуляції границя таких областей визначається граничним пристроєм, що розділяє сигнали за рівнем, а при частотній модуляції – смуговими фільтрами.
сигналу. Так при амплітудній модуляції границя таких областей визначається граничним пристроєм, що розділяє сигнали за рівнем, а при частотній модуляції – смуговими фільтрами.
Правдиве «положення» сигналів 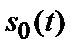 і
і  в цьому просторі зображено відповідними точками
в цьому просторі зображено відповідними точками 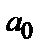 і
і  (рис. 1). Кожної з можливих реалізацій прийнятого сигналу відповідає точка в просторі сигналів, що у загальному випадку не збігається з
(рис. 1). Кожної з можливих реалізацій прийнятого сигналу відповідає точка в просторі сигналів, що у загальному випадку не збігається з 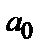 і
і  , що обумовлено впливом завад. Під їхнім впливом прийнятий сигнал може виявитися як у «своєму», так і в «сусіднім» підпросторі, що приведе до виникнення помилки прийому. По прийнятій реалізації
, що обумовлено впливом завад. Під їхнім впливом прийнятий сигнал може виявитися як у «своєму», так і в «сусіднім» підпросторі, що приведе до виникнення помилки прийому. По прийнятій реалізації 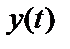 можна лише судити про величину імовірності, з яким був переданий сигнал
можна лише судити про величину імовірності, з яким був переданий сигнал 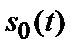 або
або  , тобто єдине, що виявляється можливим на прийомній стороні – це визначити умовні імовірності
, тобто єдине, що виявляється можливим на прийомній стороні – це визначити умовні імовірності  і
і 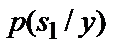 по відомому
по відомому  .
.
|
|
|
| |
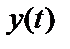 може бути прийняте рішення про справедливість однієї з двох гіпотез – гіпотеза
може бути прийняте рішення про справедливість однієї з двох гіпотез – гіпотеза 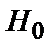 про прийом символу «0» і гіпотеза
про прийом символу «0» і гіпотеза  про прийом символу «1», по максимуму апостеріорної імовірності
про прийом символу «1», по максимуму апостеріорної імовірності
| L |
 .
.
У припущенні  (рівномірний закон розподілу
(рівномірний закон розподілу  ) і рівності апріорних (умовних) імовірностей
) і рівності апріорних (умовних) імовірностей  (
(  ) більш ймовірна гіпотеза
) більш ймовірна гіпотеза  визначається по максимуму функції правдоподібності
визначається по максимуму функції правдоподібності  ).
).
При ухваленні рішення для випадку двійкових сигналів можливі наступні ситуації:
- передано сигнал 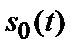 (
( 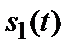 ), прийнята гіпотеза
), прийнята гіпотеза 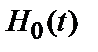 (
(  ) – правильний прийом (правильне виявлення «0» («1»)). Імовірності цих подій рівні:
) – правильний прийом (правильне виявлення «0» («1»)). Імовірності цих подій рівні:
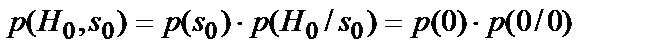 ;
;
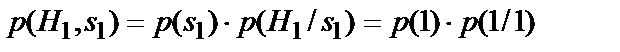 ;
;
- передано сигнал 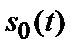 (
( 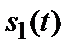 ), прийнятий
), прийнятий 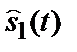 (
( 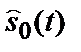 ) – прийом з помилкою. Імовірності цих подій рівні:
) – прийом з помилкою. Імовірності цих подій рівні:
 –
–
помилка «другого роду», відповідає ситуації, коли переданий «0», а прийняте рішення про те, що передано «1»;
 –
–
помилка «першого роду», відповідає ситуації, коли передана «1», а прийняте рішення про те, що передано «0».
При передачі дані помилки 1-го і 2-го роду в однаковому ступені погіршують якість роботи системи. У загальному випадку співвідношення між такими помилками залежить від характеру розбивки простору сигналів на відповідні області і задається ваговими коефіцієнтами  і
і 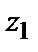 . У цих умовах зручним і об'єктивним показником кількісної оцінки завадостійкості систем передачі повідомлень є величина виду
. У цих умовах зручним і об'єктивним показником кількісної оцінки завадостійкості систем передачі повідомлень є величина виду
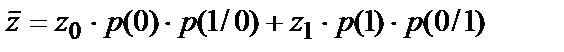 , (1)
, (1)
а критерієм оптимальності приймача є мінімізація  (1).
(1).
При передачі двійкових сигналів очевидна рівність  через однакову важливість правильного прийому і «0», і «1». Тоді вираження (1) приймає вид:
через однакову важливість правильного прийому і «0», і «1». Тоді вираження (1) приймає вид:
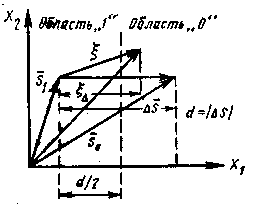 Рис. 2. До визначення потенційної завадостійкості
Рис. 2. До визначення потенційної завадостійкості
|
 . (2)
. (2)|
|
|
| L=| DS | |
Відстань  між кінцями векторів сусідніх сигналів є геометричною інтерпретацією розходження між сигналами, що відповідають «0» і «1». Чим більше
між кінцями векторів сусідніх сигналів є геометричною інтерпретацією розходження між сигналами, що відповідають «0» і «1». Чим більше  , тим більше потенційна завадостійкість. Величина
, тим більше потенційна завадостійкість. Величина 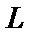 залежить від рівнів сусідніх сигналів та від способу перетворення повідомлення в сигнал.
залежить від рівнів сусідніх сигналів та від способу перетворення повідомлення в сигнал.
Як було показано вище, максимізація кількості інформації, переданої по каналу зв'язку, можлива при  . Звідси (2) перетвориться до виду
. Звідси (2) перетвориться до виду
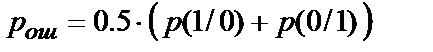 , (3)
, (3)
а при 
 . (4)
. (4)
У цих умовах алгоритм ухвалення рішення (вирішальне правило) полягає в обчисленні відносини правдоподібності:
 , (5)
, (5)
де 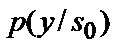 і
і 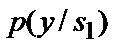 – функції правдоподібності, і порівнянні його з одиницею.
– функції правдоподібності, і порівнянні його з одиницею.
Якщо  , то приймається рішення, що передавалася одиниця, у противному випадку – нуль.
, то приймається рішення, що передавалася одиниця, у противному випадку – нуль.
Геометричний смисл критерію (5) при прийомі двійкових повністю відомих сигналів полягає в тому, що переданим вважається той символ, точка відображення якого (  або
або 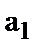 ) знаходиться ближче до точки, що відображає реалізацію прийнятого коливання
) знаходиться ближче до точки, що відображає реалізацію прийнятого коливання 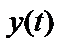 (див. рис. 1).
(див. рис. 1).
Отже, що вирішує правило оптимального приймача можна записати у виді:
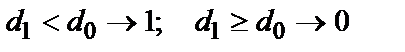 . (6)
. (6)
Відповідно до цього правила прийомний пристрій повинний розділити весь простір сигналів на два непересічні підпростори ( 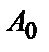 і
і  ) сигналів і визначити, у якій області знаходиться точка
) сигналів і визначити, у якій області знаходиться точка 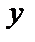 . Якщо вона знаходиться в підпросторі
. Якщо вона знаходиться в підпросторі  , то приймається рішення, що передавалася «1», у противному випадку – «0».
, то приймається рішення, що передавалася «1», у противному випадку – «0».
|
|
|
Нехай 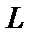 – відстань між точками
– відстань між точками  і
і  . Тоді при рівноймовірних сигналах
. Тоді при рівноймовірних сигналах 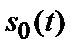 і
і  правило (6) рівнозначно перевірці умови
правило (6) рівнозначно перевірці умови 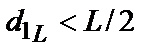 (або
(або  ). У випадку його істинності приймається рішення про передачу «1», у противному випадку – «0». Величина
). У випадку його істинності приймається рішення про передачу «1», у противному випадку – «0». Величина 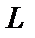 (див. рис. 2) однозначно визначається параметрами сигналу: його тривалістю
(див. рис. 2) однозначно визначається параметрами сигналу: його тривалістю 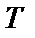 , частотою
, частотою  , що характеризує ширину його спектра (
, що характеризує ширину його спектра (  ), і середньою потужністю
), і середньою потужністю  .
.
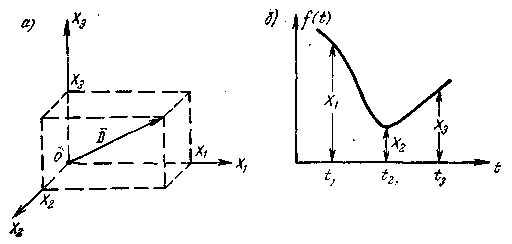 Рис. 3. Представлення сигналу в тривимірному просторі:
а) геометричне представлення сигналу; б) функція, що описує сигнал.
Рис. 3. Представлення сигналу в тривимірному просторі:
а) геометричне представлення сигналу; б) функція, що описує сигнал.
|
 із шириною спектра
із шириною спектра 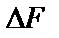 однозначно визначається
однозначно визначається  відліками (числами), що є ординатами, отриманими через інтервали
відліками (числами), що є ординатами, отриманими через інтервали  . Кожному такому сигналові може бути поставлена у відповідність одна точка в просторі з
. Кожному такому сигналові може бути поставлена у відповідність одна точка в просторі з 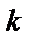 вимірів, що називається простором сигналів, або вектор
вимірів, що називається простором сигналів, або вектор  , що з'єднує цю точку з початком координат. Довжина (норма) цього векторові дорівнює
, що з'єднує цю точку з початком координат. Довжина (норма) цього векторові дорівнює
 ,
, 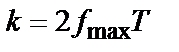 , (7)
, (7)
де 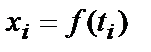 – координата точки по осі
– координата точки по осі 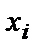 , тобто значення сигналу в момент часу
, тобто значення сигналу в момент часу  (
(  ).
).
Приклад геометричного представлення 3-х відліків (  ,
, 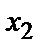 ,
,  ) у моменти часу
) у моменти часу  ,
, 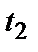 ,
, 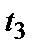 функції
функції 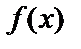 (рис. 3, б) приведений на рис. 3, а.
(рис. 3, б) приведений на рис. 3, а.
Представимо функцію 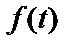 , що описує залежність від часу
, що описує залежність від часу 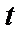 напруги реалізації сигналу, обмеженого по спектру (у межах
напруги реалізації сигналу, обмеженого по спектру (у межах  ), поруч Котельникова виду
), поруч Котельникова виду
 ,
,
де
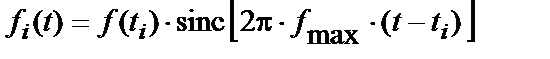 ,
,  . (8)
. (8)
Енергія доданку 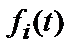 (8) дорівнює
(8) дорівнює

 ,
,
а повна енергія, що виділяється сигналом на одиничному опорі, –
 ,
,  .
.
З огляду на (8) і приймаючи до уваги ортогональність функцій відліку 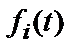 , з (7) легко одержати
, з (7) легко одержати
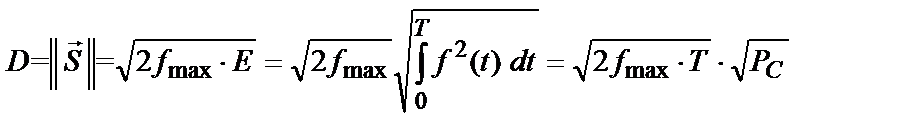 , (9)
, (9)
де  – середня потужність сигналу, тобто при заданій ширині спектра (
– середня потужність сигналу, тобто при заданій ширині спектра (  ) і тривалості (
) і тривалості (  ) сигналу довжина вектора (
) сигналу довжина вектора ( 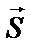 ), що відображає сигнал у
), що відображає сигнал у  - мірному просторі його дискретних відліків, пропорційна діючому (середньоквадратичному) значенню його напруги (
- мірному просторі його дискретних відліків, пропорційна діючому (середньоквадратичному) значенню його напруги ( 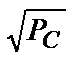 ).
).
Білет №17
1. Прості різновиди завадостійких кодів
2. Загальна характеристика методів фізичного кодування інформації
Відповіді
|
|
|
|
|
|


