 |
Свойства плотности распределения двумерной случайной величины
|
|
|
|
1) Плотность распределения двумерного случайного вектора есть функция неотрицательная:
. (15)
Действительно, по определению плотность распределения есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника – и, следовательно, отрицательной быть не может.
2) Вероятность попадания случайной точки (X,Y) в область D равна двойному интегралу от плотности по области D:
(16)
Действительно, разбив область D на прямоугольники и применив к каждому из них равенство (13), получаем, по теореме сложения вероятностей, при стремлении к нулю площадей прямоугольников (то есть при 
и 
), формулу (15). Геометрически эта вероятность изображается объёмом цилиндрического тела, ограниченного сверху поверхностью распределения 
и опирающегося на область D.
3) Функция распределения двумерной случайной величины выражается через плотность распределения следующим образом:
(17)
Эта формула следует из (13), так как F(x,y) есть вероятность попадания в прямоугольник, ограниченный абсциссами 
и ординатами 
.
4) Условие нормировки: двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице:
. (18)
Действительно, этот интеграл есть вероятность попадания во всю плоскость xOy, то есть вероятность достоверного события. Геометрически свойство 4 означает, что объём тела, ограниченного поверхностью распределения и плоскостью xOy, равен единице.
5) Плотности распределения компонент двумерного случайного вектора могут быть получены по формулам:
, (19)
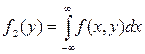. (20)
Доказательство. Принимая во внимание, что
и 
,
найдем
.
Продифференцировав обе части этого равенства по х, получим формулу (19):
|
|
|
.
Аналогично выводится формула (20).
Пример 5. Двумерная случайная величина (X,Y) задана плотностью распределения вероятностей 
.
Найти: 1) А; 2) 
; 3) 
и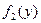 
.
Решение: 1) Постоянную А найдём, используя условие нормировки:
, 
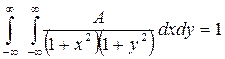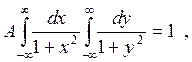
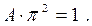
Следовательно, 
2) Используя формулу (14), находим:
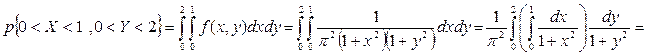
Можно было сначала по формуле (17) найти функцию распределения
и затем воспользоваться формулой (8):
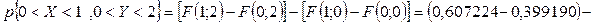
3) 
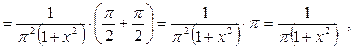
Ответ:
1) 
; 2) 
0,088104; 3)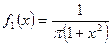 
; 
.
Система n случайных величин
Перейдём теперь к системе n случайных величин или к n-мерной случайной величине.
Функция распределения n-мерной случайной величины - это вероятность совместного выполнения неравенств вида: {Xi<xi}:
F(x1, x2, …, xn) = p{ X1<x1; X2<x2; …; Xn<xn}. (21)
Свойства функции распределения аналогичны двумерному случаю, в частности:
; 
; 
. (22)
Закон распределения дискретной n-мерной случайной величины - это совокупность всех возможных значений, которые может принимать n-мерная случайная величина, и их вероятностей:
. (23)
Для непрерывной n-мерной случайной величины вводят понятие плотности распределения.
Плотность распределения n-мерной случайной величины 
– это n-ная смешанная частная производная функции распределения 
, взятая один раз по каждому аргументу:
. (24)
При этом: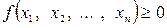 
, (25)
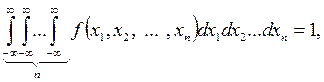(26)
(27)
Функция распределения выражается через плотность n -кратным интегралом
(28)
Зависимость и независимость случайных величин
Ранее было показано, как, зная закон распределения вероятностей системы двух случайных величин (двумерного вектора), определить законы распределения отдельных случайных величин, входящих в систему (то есть компонент вектора).
Естественно, возникает вопрос: нельзя ли по законам распределения вероятностей отдельных величин, входящих в систему, найти закон распределения системы? Оказывается, в общем случае этого сделать нельзя. Это можно сделать только в том случае, когда случайные величины X и Y независимы.
|
|
|
|
|
|
