 |
Условные законы распределения
|
|
|
|
Обратимся теперь к зависимым величинам. Вероятностная зависимость между случайными величинами часто встречается на практике. Если случайные величины X и Y находятся в вероятностной зависимости, это не означает, что с изменением величины X величина Y изменяется вполне определенным образом; это лишь означает, что с изменением величины X величина Y имеет тенденцию также изменяться (например, возрастать или убывать с ростом X). Эта тенденция соблюдается лишь в общих чертах, и в каком-то отдельном случае от неё возможны отступления. Примеры случайных величин, находящихся в вероятностной зависимости: рост и возраст ребенка; затраты и прибыль при производстве определенной продукции; затраты на рекламу и объем продаваемой продукции.
Для того, чтобы полностью описать систему, недостаточно знать распределение каждой из составляющих; нужно ещё знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью условных законов распределения.
Условным законом распределения одной из случайных величин, входящих в систему (X,Y), называется её закон распределения, найденный при условии, что другая случайная величина приняла определённое значение (или попала в какой-то интервал).
Пусть (X,Y) – дискретная двумерная случайная величина и
В соответствии с определением условных вероятностей событий*), условная вероятность того, что случайная величина Х примет значение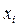 
при условии 
, определяется равенством
(34)
Совокупность вероятностей (34), то есть 
, представляет собой условный закон распределения случайной величины Х при условии . Сумма условных вероятностей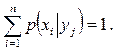 
Аналогично определяются условная вероятность и условный закон распределения случайной величины Y при условии 
:
|
|
|
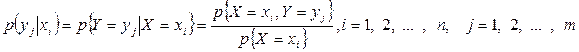. (35)
Пример 8. Пусть закон распределения двумерного случайного вектора (X,Y) задан таблицей 2 (стр. 8). Найти условный закон распределения случайной величины Х при Y =0,1.
Решение. С учетом формулы (34) имеем:
(значение 
взято из безусловного закона распределения случайной величины Y, приведенного в таблице 4 на стр. 9).
*) Пусть А и В – случайные события. Тогда вероятность их совместного появления равна 
, где 
- условная вероятность события В при условии, что событие А произошло; 
- условная вероятность события А при условии, что событие В произошло. Тогда 
, 
.
Таким образом, условный закон распределения случайной величины Х при Y =0,1 таков:
Таблица 5
 Х
| |||
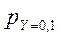
| 0,4 | 0,6 |
Сравнивая найденный условный закон распределения случайной величины Х с безусловным законом её распределения (таблица 3 на стр. 8), видим, что они различны. Следовательно, случайные величины X и Y находятся в вероятностной зависимости.
Пусть теперь (X,Y) – непрерывная двумерная случайная величина с плотностью 
; 
и 
- плотности распределения соответственно случайной величины Х и случайной величины Y.
Условной плотностью распределения составляющей X при условии Y=y называют отношение плотности совместного распределения к плотности распределения составляющей Y:
(36)
Аналогично определяется условная плотность распределения составляющей Y при условии X=x:
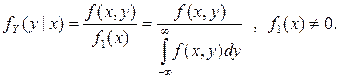(37)
Из (36) и (37) получим:
. (38)
Таким образом, плотность распределения системы двух непрерывных случайных величин равна произведению плотности одной составляющей на условную плотность другой составляющей.
Как и любая плотность распределения, условные плотности обладают следующими свойствами:
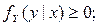
(39)
Пример 9. Непрерывный вектор (X,Y) равномерно распределен в круге с радиусом 1, то есть
Найти условные плотности распределения компонент этого вектора.
|
|
|
Решение
Условную плотность составляющей Х при 
найдём по формуле (36):
Так как 
при 
, то 
при 
.
Аналогично находим:
; 
при 
Итак, искомые условные плотности распределения составляющих системы (X,Y) имеют вид:
Для независимых случайных величин условная плотность распределения совпадает с безусловной плотностью распределения. Действительно,
(40)
Аналогично 
(41)
Степень зависимости между случайными величинами обычно оценивают с помощью числовых характеристик зависимости.
|
|
|
