 |
Двумерное нормальное распределение
|
|
|
|
В теории вероятностей и её приложениях большую роль играет двумерное нормальное распределение. Плотность двумерной нормальной случайной величины (X,Y) имеет вид
 (52)
(52)
Здесь  - математические ожидания величин X и Y;
- математические ожидания величин X и Y;  - средние квадратичные отклонения величин X и Y; r – коэффициент корреляции величин X и Y.
- средние квадратичные отклонения величин X и Y; r – коэффициент корреляции величин X и Y.
Предположим, что случайные величины X и Y не коррелированы, то есть r=0. Тогда имеем:
 (53)
(53)
Получили, что плотность распределения системы двух случайных величин (X,Y) равна произведению плотностей распределения компонент X и Y, а это значит, что X и Y – независимые случайные величины.
Таким образом, доказана следующая теорема: из некоррелированности нормально распределенных случайных величин следует их независимость. Поскольку из независимости любых случайных величин следует их некоррелированность, то можно сделать вывод, что термины «некоррелированные» и «независимые» величины для случая нормального распределения эквивалентны.
Приведём формулы для вероятности попадания нормально распределённой двумерной случайной величины в различные области на плоскости.
Пусть случайный вектор (X,Y), компоненты которого независимы, распределён по нормальному закону (53). Тогда вероятность попадания случайной точки (X,Y) в прямоугольник R, стороны которого параллельны координатным осям, равна
 y y
 R R
         d d
  c c
  х
х
 a b
a b
|   (54) (54)


|
где  - функция Лапласа. Эта функция табулирована.
- функция Лапласа. Эта функция табулирована.
Пусть плотность распределения нормального закона системы случайных величин (X,Y) задана в виде (52). Ясно, что данная плотность сохраняет постоянное значение на эллипсах:
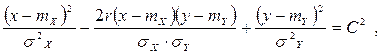 (55)
(55)
где С – постоянная; на этом основании такие эллипсы носят название эллипсов равных вероятностей. Можно показать, что вероятность попадания точки (X,Y) внутрь эллипса равной вероятности равна
|
|
|
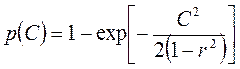 (56)
(56)
Пример 10. Случайные величины X и Y независимы и нормально распределены с  Найти вероятность того, что случайная точка (X,Y) попадет в кольцо
Найти вероятность того, что случайная точка (X,Y) попадет в кольцо 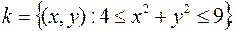
Решение: Так как случайные величины X и Y независимы, то они не коррелированы и, следовательно, r = 0. Подставляя  в (С), получаем
в (С), получаем
 ,
,
то есть эллипс равной вероятности выродился в круг равной вероятности. Тогда
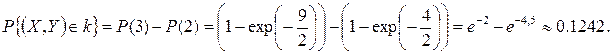
Ответ: 0,1242.
3.2. Общий случай n-мерного нормального распределения
Плотность нормального распределения системы n случайных величин имеет вид:
 , (57)
, (57)
где  - определитель матрицы С - обратной к ковариационной матрице;
- определитель матрицы С - обратной к ковариационной матрице; 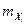 - математическое ожидание случайной величины Хi - i-той компоненты n -мерного нормального случайного вектора.
- математическое ожидание случайной величины Хi - i-той компоненты n -мерного нормального случайного вектора.
Из общего выражения вытекают все формы нормального закона для любого числа измерений и для любых видов зависимости между случайными величинами. В частности, при n = 2 ковариационная матрица имеет вид:
 (58)
(58)
её определитель 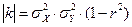 ; матрица С, обратная к ковариационной матрице, имеет вид
; матрица С, обратная к ковариационной матрице, имеет вид
 . (59)
. (59)
Подставляя  и элементы матрицы С в общую формулу (57), получаем формулу для нормального распределения на плоскости (52).
и элементы матрицы С в общую формулу (57), получаем формулу для нормального распределения на плоскости (52).
Если случайные величины 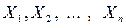 независимы, то плотность распределения системы
независимы, то плотность распределения системы  равна
равна
 . (60)
. (60)
При n = 2 эта формула принимает вид (53).
3.2. Функции от нормально распределенных случайных величин. Распределения хи-квадрат, Стьюдента, Фишера- Снедекора
Рассмотрим общий случай: линейную функцию от нормально распределенных аргументов. Пусть дан n-мерный нормально распределенный случайный вектор  , случайная величина Y представляет собой линейную функцию от этих величин:
, случайная величина Y представляет собой линейную функцию от этих величин:
 (61)
(61)
Можно показать, что случайная величина Y также распределена нормально с параметрами
 (62)
(62)
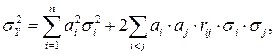 (63)
(63)
где  – математическое ожидание случайной величины
– математическое ожидание случайной величины 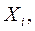
 - дисперсия случайной величины
- дисперсия случайной величины 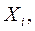
 - коэффициент корреляции между
- коэффициент корреляции между  и
и  .
.
|
|
|
Пример 11. Записать плотность распределения случайной величины  , если случайные величины
, если случайные величины 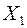 и
и  имеют нормальное распределение с параметрами
имеют нормальное распределение с параметрами 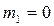 ,
,  ,
,  , их коэффициент корреляции
, их коэффициент корреляции  .
.
Решение. По условию задачи имеем: n=2; 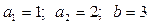 . Используя формулу (62), получаем:
. Используя формулу (62), получаем:  . Используя формулу (63), получаем:
. Используя формулу (63), получаем:  .
.
Тогда искомая функция распределения случайной величины Y имеет вид:

Пусть  - независимые случайные величины, подчиняющиеся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией, то есть стандартному нормальному распределению. Распределение случайной величины, являющейся суммой квадратов этих величин
- независимые случайные величины, подчиняющиеся нормальному распределению с нулевым математическим ожиданием и единичной дисперсией, то есть стандартному нормальному распределению. Распределение случайной величины, являющейся суммой квадратов этих величин
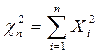 . (64)
. (64)
называется “ распределением ХИ - квадрат с n степенями свободы ”.
Плотность распределения ХИ – квадрат с n=2 степенями свободы равна
 (65)
(65)
Плотность ХИ – квадрат распределения с n степенями свободы имеет вид:
 (66)
(66)
где  - гамма-функция Эйлера. С возрастанием числа степеней свободы распределение
- гамма-функция Эйлера. С возрастанием числа степеней свободы распределение  приближается к нормальному закону распределения (при n >30 распределение
приближается к нормальному закону распределения (при n >30 распределение  практически не отличается от нормального). Математическое ожидание
практически не отличается от нормального). Математическое ожидание  - распределения c n степенями свободы равно n, а дисперсия равна 2 n.
- распределения c n степенями свободы равно n, а дисперсия равна 2 n.
Распределение Стьюдента с n степенями свободы St(n) определяется как распределение случайной величины
 , (67)
, (67)
где Z – стандартная нормальная величина, независимая от  распределения.
распределения.
Плотность распределения Стьюдента с n степенями свободы имеет вид:
 (68)
(68)
Математическое ожидание при  равно 0, дисперсия при
равно 0, дисперсия при  равна
равна  При
При  распределение Стьюдента приближается к нормальному (уже при n >30 почти совпадает с нормальным распределением).
распределение Стьюдента приближается к нормальному (уже при n >30 почти совпадает с нормальным распределением).
Распределением Фишера-Снедекора (или F-распределением) с 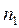 и
и  степенями свободы называется распределение случайной величины
степенями свободы называется распределение случайной величины
 (69)
(69)
где  и
и 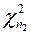 - случайные величины, имеющие
- случайные величины, имеющие  - распределение с
- распределение с  и
и  степенями свободы, соответственно.
степенями свободы, соответственно.
Плотность распределения Фишера-Снедекора при 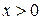 имеет вид:
имеет вид:
 . (70)
. (70)
Математическое ожидание при  равно
равно  , дисперсия при
, дисперсия при 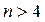 равна
равна  . При
. При  F - распределение стремится к нормальному закону.
F - распределение стремится к нормальному закону.
Распределения ХИ - квадрат, Стьюдента, Фишера - Снедекора используются в математической статистике.
Список литературы
1. Гмурман В.Е. / Теория вероятностей и математическая статистика. – М.: «Высшая школа”, 1977.
|
|
|
2. Гмурман В.Е. / Руководство к решению задач по теории вероятностей и математической статистике. – М.: ”Высшая школа”, 1975.
3. Вентцель Е.С. / Теория вероятностей. – М.: Гос.изд-во физ.-мат. лит-ры, 1962.
4. Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. – М.: Айрис-пресс, 2004.
Содержание
1. Основные сведения о системах случайных величин и о способах их задания.. 3
1.1. Понятие о системе случайных величин.............................. 3
1.2. Функция распределения вероятностей двумерной случайной величины и её
свойства....................................................... 4
1.3. Закон распределения вероятностей дискретной двумерной случайной величины.......................................................... 7
1.4. Плотность распределения вероятностей непрерывной двумерной случайной величины и её свойства........................................... 9
1.5. Система n случайных величин.................................... 13
2. Зависимость и независимость случайных величин....................... 14
2.1. Независимые случайные величины................................. 14
2.2. Условные законы распределения................................... 15
2.3. Числовые характеристики зависимости............................. 19
3. Нормальное распределение системы случайных величин................ 22
3.1. Двумерное нормальное распределение............................. 22
3.2. Общий случай n-мерного нормального распределения................ 24
3.3. Функции от нормально распределенных случайных величин. Распределения ХИ - квадрат, Стьюдента, Фишера - Снедекора................... 25
Список литературы................................................... 27
Составитель Бобкова Вера Александровна
Системы случайных величин
Методические указания для самостоятельной работы студентов
Редактор Г.В.Куликова
Подписано в печать 02.03.2010. Формат 60х84  . Бумага писчая. Усл.печ.л.1,63.
. Бумага писчая. Усл.печ.л.1,63.
Уч.-изд.л.1,81. Тираж 50 экз.
ГОУ ВПО Ивановский государственный химико-технологический университет
Отпечатано на полиграфическом оборудовании кафедры экономики и финансов ГОУ ВПО «ИГХТУ»
153000, г.Иваново, пр. Ф.Энгельса, 7
|
|
|
|
|
|


